




ЗАДАНИЕ 8
Нарисовать следующий рисунок.
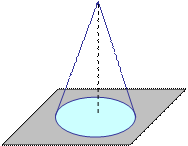
Результат сохранить в своей папке в файле с именем КОНУС.
Лабораторная работа №3. "ПРОВЕРКА ПРАВОПИСАНИЯ В WORD"
Задания
1. Прочитать с диска текст публикации и запомнить его на диске в своей папке под именем ПРОВЕРКА_ПРАВОПИСАНИЯ.
2. Установить в Word язык, используемый в публикации.
3. Осуществить проверку орфографии и грамматики текста в ручном режиме.
4. Отформатировать текст по ширине, разбивая слова на слоги при переносе.
5. Сохранить результат на диске в своей папке под именем ПРОВЕРКА_ПРАВОПИСАНИЯ.
6. Создать следующие варианты автозамены:
а) «дав» на «два»;
б) «иил» на «или»;
в) «члеовек» на «человек»;
г) «копмьтер» на «компьютер».
7. Проверить работу средства Автозамена.
8. Создать несколько вариантов Автотекста по следующим образцам:
а) ОЗУ – оперативно–запоминающее устройство;
б) БГУ – Белорусский государственный университет;
в) ГИУСТ – Государственный институт управления и социальных технологий;
г) подпись –
Заведующий кафедрой математического
Обеспечения АСУ, д.т.н., профессор Совпель И. В.
д) подготовить для деловых бумаг блок “Утверждаю”.

9. Внести в некоторую публикацию созданные в п. 8 варианты автотекста.
Лабораторная работа №4. “РАБОТА С РЕДАКТОРОМ
ФОРМУЛ MICROSOFT EQUATION 3.0”
Задания
1. Используя средства Редактора формул , создать документы с формульными фрагментами:
а) по образцу 1;
б) по образцу 2;
б) по образцу 3 (воспользоваться только средствами Microsoft Word, а не редактора формул);
в) по образцу 4 (воспользоваться только средствами Microsoft Word, а не редактора формул);
г) по образцу 5;
д) по образцу 6;
е) по образцу 7.
2. Оформить формулы, созданные по предлагаемым образцам, следующим образом:
а) вставить формулу в рамку;
б) оттенить формулу фоном.
Результат сохранить в своей папке (каждый образец в отдельный файл).
Образец 1
ФОРМУЛА 1
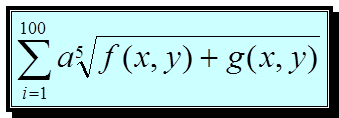
ФОРМУЛА 2
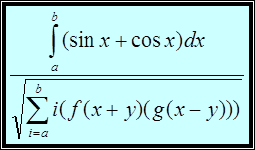
Образец 2
Система неравенств
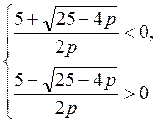
Образец 3
H2SO4 — серная кислота
H2SO3 — сернистая кислота
H2S — сероводород
BaSO4 — сульфат бария
NaOH — гидрат натрия
H2O – вода
Образец 4

Образец 5

Теорема. Решение уравнения (1) содержит max(0,a) + max(0,b) – r произвольных комплексных постоянных и находится по формуле:
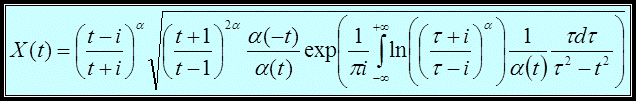
Представим матрицу SA,B в виде:
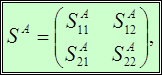
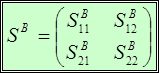
Образец 6
Электродинамические свойства специальных блоков перехода описываются матрицей рассеяния вида:
Sn = 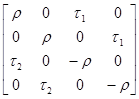
с элементами
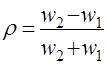 ,
, 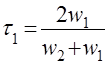 ,
, 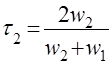 ,
,
где W1 и W2 – волновые сопротивления граничащих сред, связанные с материальными параметрами сред, заполняющих блоки, соотношениями:
W1,2 = 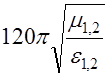 .
.
Блоки контакта с границей имеют выход на один виртуальный волновод и описываются матрицей рассеяния
Sb = 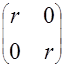 ,
,
где r = -1 для идеально проводящей стенки и r = 1 для идеальной магнитной стенки. Конечная проводимость металла может быть учтена путем использования в матрице рассеяния коэффициента отражения r вида:
r = 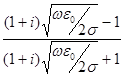
Дата: 2019-02-25, просмотров: 563.