1. Найти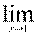

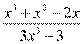
Решение:

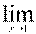
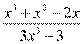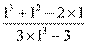 = =  -неопределенность, для раскрытия требуется дробь сократить.

Так как x=1 – корень многочленов, то многочлены кратны одночлену (x – 1):      

  x³+x²-2x x-1                                  3x³-3 x-1

  -(x³-x²) x²+2x                           -(3x³-3x²) 3x²+3x+3

       2x²-2x                                               3x²-3

     -(2x²-2x)                                              -(3x²-3x)

                0                                                     3x-3

                                                                          -(3x-3)

                                                                                  0

Разложим числитель и знаменатель на множители и сократим дробь:

Вычислим предел:

 .

Ответ:

Устранение иррациональных разностей домножением на сопряженное выражение

Примеры:

1. Найти

Решение:

При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Используя формулу  для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен ,

А затем при наличии общего множителя сократим на него дробь.

Ответ:

2. Найти

Решение:

При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Используя формулу  для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен  и , а затем при наличии общего множителя сократим на него дробь

Ответ:

3. Найти

Решение:

При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Для раскрытия неопределённости домножим числитель и знаменатель соответственно на сопряжённые двучлены  и , а затем при наличии общего множителя сократим на него дробь.

Ответ:

Замена переменной

Пример:

Найти

Решение:

При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Для раскрытия неопределённости избавимся от иррациональности сделав замену   (x=t³). Тогда при   .

Затем после преобразований сократим дробь на общий множитель.

Ответ: 4

Первый замечательный предел

Примеры:

1. Найти

Решение:

При  числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:

Ответ:

2. Найти

Решение:

При  числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:

Ответ:

3. Найти

Решение:

При  числитель и знаменатель обращаются в нуль.

Имеем неопределённость вида . Раскроем неопределённость с помощью 1-го замечательного предела после следующих преобразований:

Ответ:

Правило Лопиталя

Найти

Решение:

Ответ: 1

Неопределенность вида