Найденные в рамках теории Бора стационарные состояния атома водорода и водородоподобных ионов с учетом только круговых орбит определяются одним числом n – главным квантовым числом.

Результаты, достигнутые боровской теорией в решении задачи об энергетических уровнях электрона в водородоподобной системе, были позднее получены в рамках квантовой механики без привлечения постулатов Бора, причем оказалось, что стационарные состояния определяются целым набором квантовых чисел.

Оказывается, прежде всего, что момент импульса электрона в атоме квантуется по формуле

,

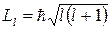где l = 0, 1, 2,..., n – 1 – орбитальное квантовое число, определяющее форму эллиптических орбит. Состояния электрона, обладающего различными значениями орбитального квантового числа, в атомной физике принято обозначать и называть следующим образом:

l =0 – s-состояние,

l =1 – р-состояние,

l =2 – d-состояние,

l =3 – f-состояние и т. д. в порядке следования букв латинского алфавита.

Значения энергии, которыми может обладать электрон в атоме, определяются выражением, совпадающим с выражением из теории Бора

.

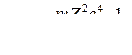Т. о., энергетические уровни электрона для водородоподобной системы зависят только от главного квантового числа.

Третье квантовое число определяет пространственное распределение траекторий движения электрона. Квантовое число m_l называют магнитным квантовым числом, так как от этого числа зависит магнитный момент, создаваемый при движении электрона по орбите.

При действии внешнего магнитного поля на атом могут осуществляться только такие ориентации орбит, при которых проекция вектора момента количества движения L_lz на направление оси z, совпадающее с направлением магнитного поля, кратна 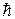 (принцип пространственного квантования):

,

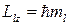где m_l  – положительное или отрицательное целое число, не превышающее по абсолютной величине l:

m_l = 0, ±1, ±2, ... ± l.

Т. о., при данных n и l  электрон в атоме, находящемся в магнитном поле, может двигаться по 2l + 1 орбитам, различающимся своей ориентацией по отношению к направлению магнитного поля.

Для полного описания движения электрона в атоме, нужно ввести еще квантовые числа, учитывающие наличие у электрона собственного момента импульса L_s (сокращенно – спинового момента, или просто спина). Из общих выводов квантовой механики следует, что спиновой момент должен быть квантован по закону

,

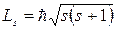где s = 1/2 – спиновое квантовое число.

По аналогии с пространственным квантованием орбитального момента импульса электрона, проекция вектора спинового момента L_sz на направление внешнего поля должна быть квантованной величиной и определяться по формуле:

,

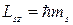где m_s = ±1/2 – магнитное спиновое квантовое число. Т. о., проекция спинового механического момента импульса на направление поля может принимать два значения:

.

Строение электронных оболочек атомов (объясняющее, в частности, периодичность химических свойств элементов) было раскрыто на основе фундаментального принципа квантовой физики, высказанного в 1924 г. швейцарским физиком Паули. В своей простейшей формулировке он гласит: в любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел: главного n, орбитального l, магнитного m_l и магнитного спинового m_s.

Применительно к системе электронов в атоме принцип Паули можно записать следующим образом:

Z₁(n, l, m_l, m_s) = 0 или 1,

где Z₁(n, l, m_l, m_s) есть число электронов, находящихся в состоянии, описываемом набором квантовых чисел n, l, m_l, m_s. Пользуясь принципом Паули, можно найти максимальное число электронов в атоме, имеющих заданные значения трех (n, l, m_l), двух (n, l) и одного (n) квантовых чисел.

Вопросы для самоконтроля:

1. Расскажите о закономерностях в атомных спектрах водорода.

2. Объясните обобщенную формулу Бальмера.

3. Что доказали опыты Резерфорда по рассеянию a-частиц.

4. Сформулируйте постулаты Бора.

5. Объясните на основании теории Бора наличие линейчатых спектров у атома водорода.

6. В чем недостатки теории Бора?

7. Сформулируйте современные представления о строении атома.

8. В чем состоит принцип Паули?