Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

J = mr ² ,

 

где m - масса материальной точки; r -расстояние от точки до оси вращения.

 

Момент инерции:

– однородного шара радиусом R и массы m (если ось вращения проходит через центр шара)

 

;

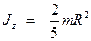– сплошного цилиндра или диска радиусом R и массы m (если ось вращения проходит через центр масс перпендикулярно плоскости основания)

 

;

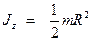– тонкого обруча или кольца радиусом R и массы m (если ось вращения проходит через центр масс перпендикулярно плоскости обруча)

J_z = mR ² ;

 

– однородного тонкого стержня длиной l и массы m (если ось вращения проходит через центр масс стержня перпендикулярно стержню)

7                                                                                                                                    8

;

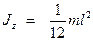– однородного тонкого стержня длиной l и массы m (если ось вращения проходит через конец стержня перпендикулярно стержню)

 

.

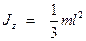Момент инерции тела массы m относительно неподвижной оси, не проходящей через центр масс и параллельной оси z

 

J = J_z + ma ² ,

 

где J_z - момент инерции тела относительно оси z; проходящей через центр масс;    a - расстояние между осями.

 

Момент силы

 

М = r × F .

Момент импульса тела

 

L = J × w .

 

Основное уравнение динамики вращательного движения твердого тела

.

 

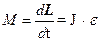Проекция момента импульса тела на неподвижную ось вращения

L_z = J_z × w .

Закон сохранения

– момента импульса для изолированной системы твердых тел

;

 

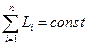
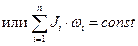– момента импульса для изолированной системы твердых тел относительно неподвижной оси вращения z

 

.

 

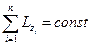
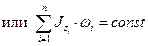Работа постоянного момента внешних сил при вращении твердого тела

A = M_z j ,

 

где j - угол поворота.

 

Мощность, развиваемая моментом внешних сил

.

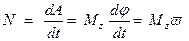Кинетическая энергия тела, вращающегося вокруг неподвижной оси z

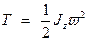 или .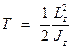

 

Кинематическое уравнение гармонических колебаний материальной точки

	9                                                                                                                               10

x = Acos( w t+ j _o )

{x = Asin( w t+ j _o )},

 

где x - смещение колеблющейся точки от положения равновесия; A – амплитуда; w - круговая (циклическая) частота; j_o - начальная фаза колебаний.

 

Скорость материальной точки, совершающей гармонические колебания

 

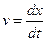= -A w sin( w t+ j _o )

{v = A w cos( w t+ j _o )}.

 

Ускорение материальной точки, совершающей гармонические колебания

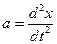= -A w ² cos( w t+ j _o )

{a = -A w ² sin( w t+ j _o )}.

Динамическое уравнение гармонических колебаний

 

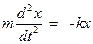 или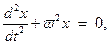

где .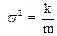

Полная механическая энергия материальной точки, совершающей гармонические колебания

.

 

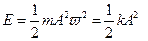Период колебаний маятника:

 

– пружинного

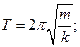
– математического

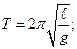
– физического

 

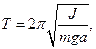
где J - момент инерции маятника; a - расстояние от центра масс маятника до оси колебаний.

 

Уравнение затухающих колебаний

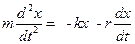 или ,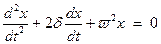

 

где r - коэффициент сопротивления среды; d = 2r/m - коэффициент затухания; w - частота затухающих колебаний.