1. Проверка на прочность.
В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ, после чего максимальная из них сравнивается с заданным допустимым значением [σ].
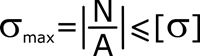
Ответ в данной задаче дается в виде заключения:
· если σmax ≤ [σ] стержень прочный,
· если σmax > [σ] стержень непрочный.
2. Подбор размеров сечения (проектировочный расчет)
Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.
Для этого условие прочности записывается относительно искомой величины.
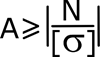
Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.
3. Определение грузоподъемности стержня.
Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.
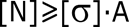
В данном случае условие прочности записано относительно внутренней силы N.
24. Запишите формулу для определения касательных напряжений в поперечных
Сечениях балки при прямом поперечном изгибе?
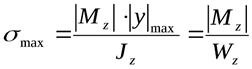
 ;.
;.
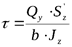 формула Журавского
формула Журавского
Как находятся главные напряжения при изгибе?
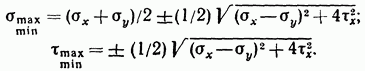
Как направлены главные площадки на уровне нейтрального слоя и в точках,
Наиболее удаленных от этого слоя?
Какие формы поперечных сечений являются рациональными для балок из
Пластичных материалов?
Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным. Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки. Иными словами необходимо, чтобы наибольшие напряжения растяжения (max sр) н наибольшие напряжения сжатия (max sс) одновременно достигали допускаемых напряжений [sр] и [sс].
Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: [sр] = [sс] = [s]), условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение, при котором обеспечено условие равенства maxsр=maxsс. Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра , у которого возможно большая часть материала сосредоточена на полках (горизонтальных массивных листах), соединенных стенкой (вертикальным листом), толщина которой (d) назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости . К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение.
28. Какие перемещения получают поперечные сечения балок при прямом изгибе? Согласно гипотезе Бернулли поперечные сечения балки при прямом изгибе не искривляются, а лишь вертикально смещаются, поворачиваясь при этом относительно нейтральной линии на некоторый угол. Таким образом, перемещениями при изгибе являются вертикальное смещение (прогиб) сечений 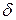 и угол поворота сечений
и угол поворота сечений 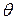 , причем функция углов поворота связана с функцией прогибов дифференциальной зависимостью. Поэтому из двух функций перемещений основной является функция прогибов.
, причем функция углов поворота связана с функцией прогибов дифференциальной зависимостью. Поэтому из двух функций перемещений основной является функция прогибов.
29. Запишите основное дифференциальное уравнение изогнутой оcи балки. 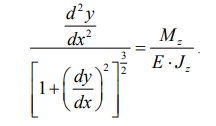
Дата: 2019-02-19, просмотров: 492.