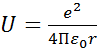
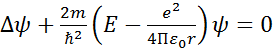 – уравнение Шредингера.
– уравнение Шредингера.
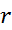 – радиус окружности (расстояние от протона до нейтрона)
– радиус окружности (расстояние от протона до нейтрона)
Это уравнение имеет решение, удовлетворяющее требованиям конечности однозначностей функции только при определенных значениях полной энергии атома.
|
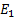
|
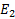
|
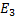
|
| 0 |
| E |
| U |
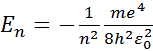
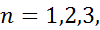 … – главное квантовое число
… – главное квантовое число
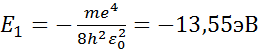
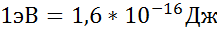
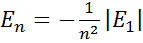
Волновая функция определяется тремя квантовыми числами:
1. 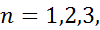 … – главное квантовое число
… – главное квантовое число
2.Орбитальное квантовое число 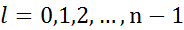 определяет орбитальный импульс электрона
определяет орбитальный импульс электрона
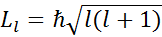
3. 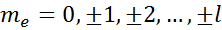 магнитное квантовое число, определяет квантовые проекции орбитального момента импульса на выделенное направление
магнитное квантовое число, определяет квантовые проекции орбитального момента импульса на выделенное направление
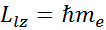
Полная энергия атома водорода зависит только от главного квантового числа.
Вырожденные состояния – это различные квантовые состояния, которые имеют одинаковую энергию.
Кратность вырождений – это число различных квантовых состояний.
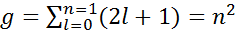
Сериальные з акономерности в спектре атома водорода.
Квантовые решения вытекают из уравнения Шредингера.
Квантовый переход – скачкообразный переход системы из одного энергетического уровня на другой. Если атом с меньшей энергией переходит на любой другой уровень – происходит поглощение энергии. Если атом с большей энергией переходит в состояние с меньшей энергией – происходит испускание электрона.
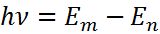
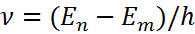
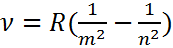 – формула Бальмера-Ридберга, а серия, описываемая ей – серией Бальмера.
– формула Бальмера-Ридберга, а серия, описываемая ей – серией Бальмера. 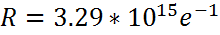 – постоянная Ридберга
– постоянная Ридберга
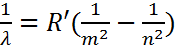
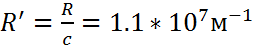
 Энергетический спектр атома водорода
Энергетический спектр атома водорода
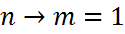 серия Лаймана
серия Лаймана
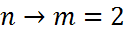 серия Бальмера
серия Бальмера
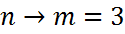 серия Пашена
серия Пашена
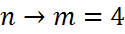 серия Брэкета
серия Брэкета
Спин электрона. Опыт Штерна и Герлаха.
Опыт Штерна и Герлаха:
| - |
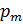
|
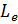
|
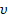
|
Правило пространственного квантования:
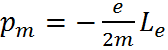
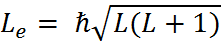 – собственный момент
– собственный момент
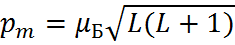 – магнитный момент
– магнитный момент
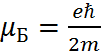
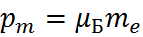 – проекция
– проекция
Спин электрона – квантовая величина, не имеющая классического аналога. Это внутреннее неотъемлемое свойство электрона, такое же как заряд и масса.
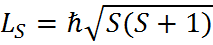
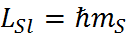
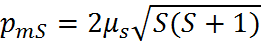
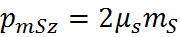 ,
, 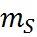 – спиновое магнитное квантовое число
– спиновое магнитное квантовое число
Для электрона 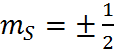
Многоэлектронный атом. Схема уровней энергии и оптические спектры. Правила отбора.
Движение электрона в атоме описывается уравнением Шредингера.
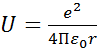
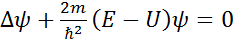 – уравнение Шредингера.
– уравнение Шредингера.
Одноэлектронное приближение:
| - |
| Атом остаток |
Основной результат решения уравнения Шредингера:
Полная энергия электрона в многоэлектронном атоме зависит от главного и орбитального квантового числа.
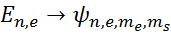
Вырождение по квантовому числу 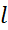 считается.
считается.
Схема уровней для атома водорода:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| n(∞) |
|
| H |
| 1 – 1s |
| 2 – 2s |
| 2.1 – 2p |
| 3 – 3s |
| 3.1 – 3p |
| 3.2 – 3d |
| Многоэлектронный атом |
| 0 | 1 | 2 | 3 | 4 |
| Обозн. | s | p | d | f | g |
Правила отбора ограничивают число возможных квантовых переходов. Существует правило отбора по орбитальному квантовому числу:
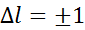
Дата: 2019-02-19, просмотров: 316.