| № варианта | Система | № варианта | Система |
| 1. | 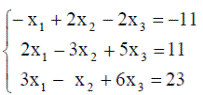
| 2. | 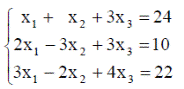
|
| 3. | 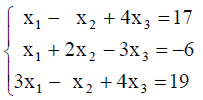
| 4. | 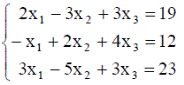
|
| 5. | 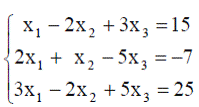
| 6. | 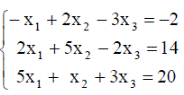
|
| 7. | 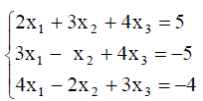
| 8. | 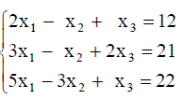
|
| 9. | 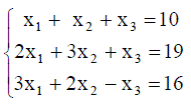
| 10. | 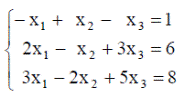
|
| 11. | 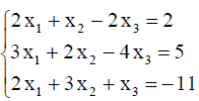
| 12. | 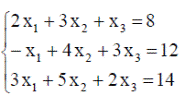
|
| 13. | 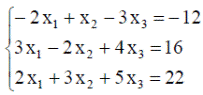
| 14. | 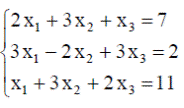
|
| 15. | 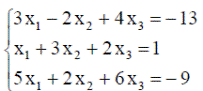
| 16. | 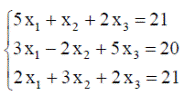
|
| 17. | 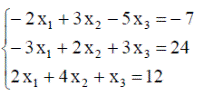
| 18. | 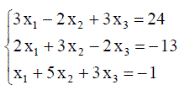
|
| 19. | 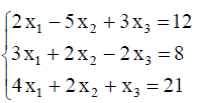
| 20. | 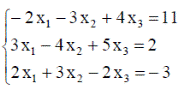
|
| 21. | 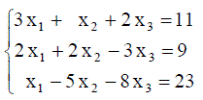
| 22. | 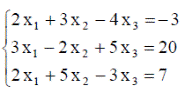
|
| 23. | 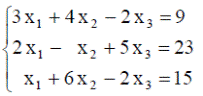
| 24. | 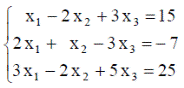
|
| 25. | 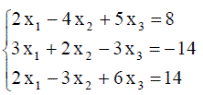
| 26. | 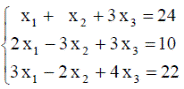
|
| 27. | 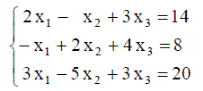
| 28. | 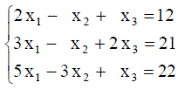
|
| 29. | 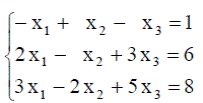
| 30. | 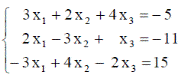
|
Задача №3. Даны точки A, B, C, D. Положим 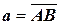 ,
, 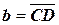 . Найти:
. Найти:
1) векторы 2а+b и а-2b;
2) модули векторов |2а+b| и |а-2b|;
3) скалярное произведение (2а+b),×(a-2b);
4) угол между векторами (2а+b)×и (a-2b).
| 1. | A(1,0,2) | B(-1,2,3) | C(2,3,1) | D(-3,4,5,) |
| 2. | A(0,3,-2) | B(4,1,3) | C(-1,1-1) | D(3,2,4) |
| 3. | A(-1,-1,0) | B(1,1,1) | C(-2,1,0) | D(0,-2,7) |
| 4. | A(0,2,0) | B(-2,0,0) | C(3,1,0) | D(0,-1,-3) |
| 5. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1) | D(2,4,1) |
| 6. | A(2,2,-1) | B(0,0,0) | C(0,-4,0) | D(2,0,0) |
| 7. | A(-3,2,4) | B(-3,-3,4) | C(0,-3,4) | D(-1,-1,4) |
| 8. | A(5,6,1) | B(6,1,4) | C(1,2,3) | D(2,0,2) |
| 9. | A(-5,6,0) | B(-6,-2,1) | C(-3,4,-1) | D(-1,-7,0) |
| 10. | A(10,9,0) | B(9,8,1) | C(8,7,1) | D(7,6,0) |
| 11. | A(7,7,0) | B(5,6,0) | C(4,5,1) | D(3,4,1) |
| 12. | A(-5,-2,0) | B(-3,-3,1) | C(0,5,0) | D(9,6,1) |
| 13. | A(-1,0,-1) | B(1,1,-1) | C(1,2,-3) | D(0,-2,-4) |
| 14. | A(1,6,2) | B(-1,0,1) | C(4,2,3) | D(-1,-1,4) |
| 15. | A(3,6,4) | B(3,5,3) | C(2,4,2) | D(1,0,1) |
| 16. | A(7,2,7) | B(9,1,7) | C(9,7,6) | D(-1,-1,7) |
| 17. | A(4,-3,2) | B(1,-7,2) | C(-1,0,1) | D(1,1,1) |
| 18. | A(0,-5,3) | B(2,2,2) | C(0,-3,1) | D(7,7,2) |
| 19. | A(1,6,7) | B(0,6,7) | C(-4,5,6) | D(-4,-4,8) |
| 20. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1) | D(2,4,1) |
| 21. | A(1,3,2) | B(4,-1,3) | C(8,1-1) | D(3,2,0) |
| 22. | A(0,2,-4) | B(-2,1,0) | C(-3,1,7) | D(0,-1,3) |
| 23. | A(2,-5,-1) | B(0,3,-9) | C(3,-4,7) | D(2,0,5) |
| 24. | A(5,-6,1) | B(4,1,-4) | C(1,-4,3) | D(-2,0,3) |
| 25. | A(1,9,0) | B(-5,8,1) | C(-3,7,1) | D(0,6,5) |
| 26. | A(5,-2,0) | B(-3-3,1) | C(7,5,4) | D(-3,6,1) |
| 27. | A(1,-6,0) | B(1,0,-1) | C(7,2,-3) | D(-1,1,4) |
| 28. | A(5,2,-7) | B(4,1,7) | C(5,-3,6) | D(1,-5,7) |
| 29. | A(-1,-5,3) | B(2,-6,0) | C(0,3,1) | D(3,7,2) |
| 30. | A(5,-6,0) | B(6,-2,1) | C(-3,4,0) | D(-1,-7,3) |
Задача №4. Даны вершины 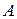 ,
, 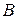 ,
, 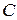 треугольника. Найти:
треугольника. Найти:
а) уравнение и длину медианы 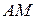 ;
;
б) уравнение и длину высоты 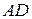 ;
;
в) угол 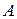 треугольника
треугольника 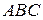 .
.
| 1. | 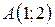 ; ; 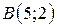 ; ; 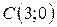 . .
|
| 2. | 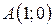 ; ;  ; ; 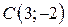 . .
|
| 3. |  ; ; 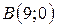 ; ; 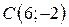 . .
|
| 4. | 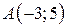 ; ; 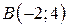 ; ; 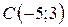 . .
|
| 5. | 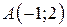 ; ; 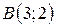 ; ; 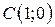 . .
|
| 6. | 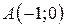 ; ;  ; ; 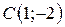
|
| 7. | 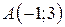 ; ; 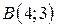 ; ; 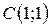 . .
|
| 8. | 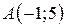 ; ; 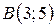 ; ; 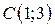 . .
|
| 9. | 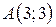 ; ; 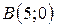 ; ; 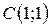 . .
|
| 10. | 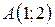 ; ; 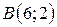 ; ; 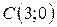 . .
|
| 11. | 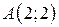 ; ;  ; ; 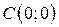 . .
|
| 12. | 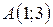 ; ; 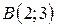 ; ; 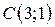 . .
|
| 13. | 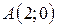 ; ; 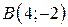 ; ; 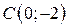 . .
|
| 14. | 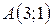 ; ; 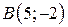 ; ; 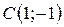 . .
|
| 15. | 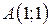 ; ; 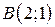 ; ; 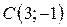 . .
|
| 16. | 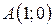 ; ;  ; ; 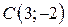 . .
|
| 17. | 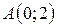 ; ; 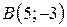 ; ; 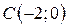 . .
|
| 18. | 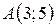 ; ; 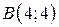 ; ; 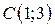 . .
|
| 19. | 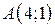 ; ;  ; ; 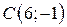 . .
|
| 20. | 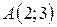 ; ; 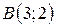 ; ; 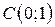 . .
|
| 21. | 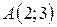 ; ; 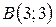 ; ; 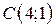 . .
|
| 22. | 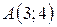 ; ; 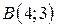 ; ; 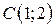 . .
|
| 23. | 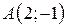 ; ; 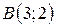 ; ; 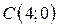 . .
|
| 24. | 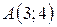 ; ; 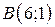 ; ; 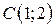 . .
|
| 25. | 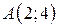 ; ; 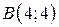 ; ; 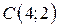 . .
|
| 26. | 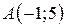 ; ; 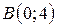 ; ; 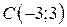 . .
|
| 27. | 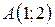 ; ; 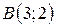 ; ; 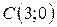 . .
|
| 28. | 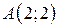 ; ; 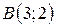 ; ; 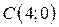 . .
|
| 29. | 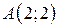 ; ;  ; ; 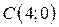 . .
|
| 30. | 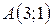 ; ; 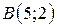 ; ; 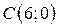 . .
|
Задача №5. Вычислить пределы
| №вар | а | б | в |
| 1 | 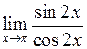
| 
| 
|
| 2 | 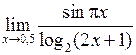
| 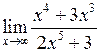
| 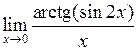
|
| 4 | 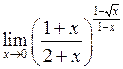
| 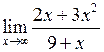
| 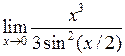
|
| 5 | 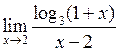
| 
| 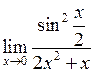
|
| 6 | 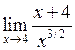 равен равен
| 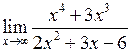
| 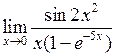
|
| 7 | 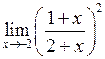
| 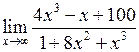
| 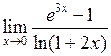
|
| 8 | 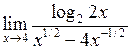
| 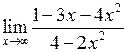
| 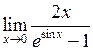
|
| 9 | 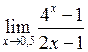
| 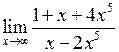
| 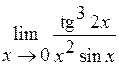
|
| 10 | 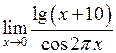
| 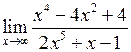
| 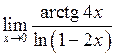
|
| 11 | 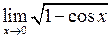
| 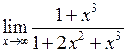
| 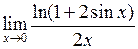
|
| 12 | 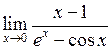
| 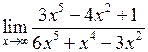
| 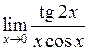
|
| 13 | 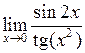
| 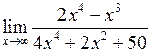
| 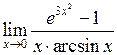
|
| 14 | 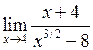
| 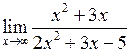
| 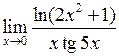
|
| 15 | 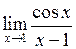
| 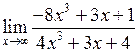
| 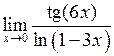
|
| 16 | 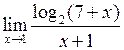
| 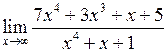
| 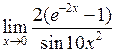
|
| 17 | 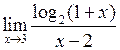
| 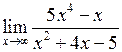
| 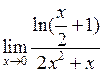
|
| 18 | 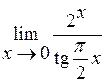
| 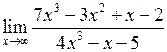
| 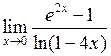
|
| 19 | 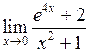
| 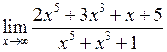
| 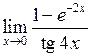
|
| 20 | 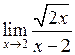
| 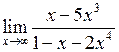
| 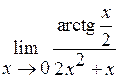
|
| 21 | 
| 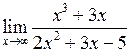
| 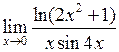
|
| 22 | 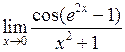
| 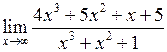
| 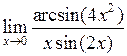
|
| 23 | 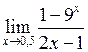
| 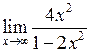
| 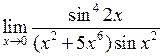
|
| 24 | 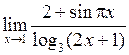
| 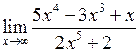
| 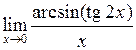
|
| 25 | 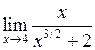
| 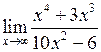
| 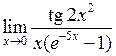
|
| 26 | 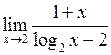
| 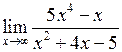
| 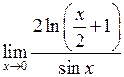
|
| 27 | 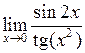
| 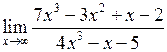
| 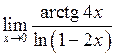
|
| 28 | 
| 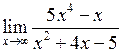
| 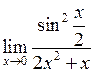
|
| 29 | 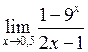
| 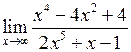
| 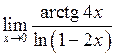
|
| 30 | 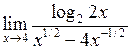
| 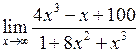
| 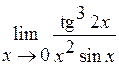
|
Задача №6. Вычислить производную функции
| №вар | a) | б) | в) |
| 1. | 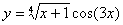
| 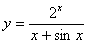
| 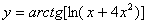
|
| 2. | 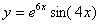
| 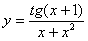
| 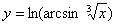
|
| 3. | 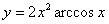
| 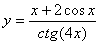
| 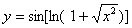
|
| 4. | 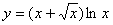
| 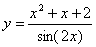
| 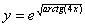
|
| 5. | 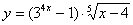
| 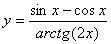
| 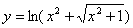
|
| 6. | 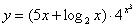
| 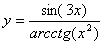
| 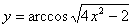
|
| 7. | 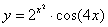
| 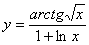
| 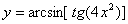
|
| 8. | 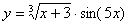
| 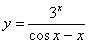
| 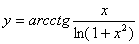
|
| 9. | 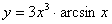
| 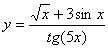
| 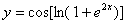
|
| 10. | 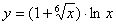
| 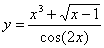
| 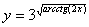
|
| 11. | 
| 
| 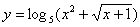
|
| 12. | 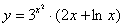
| 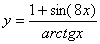
| 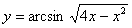
|
| 13. | 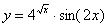
| 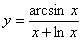
| 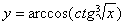
|
| 14. | 
| 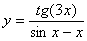
| 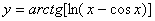
|
| 15. | 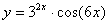
| 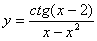
| 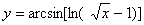
|
| 16. | 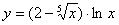
| 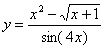
| 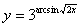
|
| 17. | 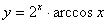
| 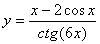
| 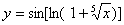
|
| 18. | 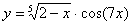
| 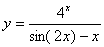
| 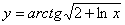
|
| 19. | 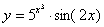
| 
| 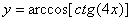
|
| 20. | 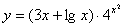
| 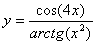
| 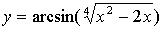
|
| 21. | 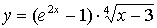
| 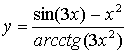
| 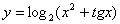
|
| 22. | 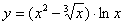
| 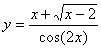
| 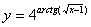
|
| 23. | 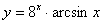
| 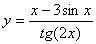
| 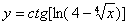
|
| 24. | 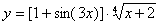
| 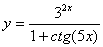
| 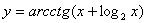
|
| 25. | 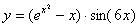
| 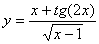
| 
|
| 26. | 
| 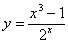
| 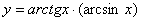
|
| 27. | 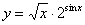
| 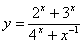
| 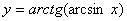
|
| 28. | 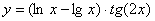
| 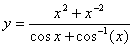
| 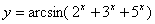
|
| 29. | 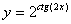
| 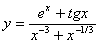
| 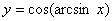
|
| 30. | 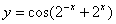
| 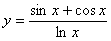
| 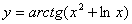
|
Задание №7. Вычислить производную второго порядка от заданной функции















КОНТРОЛЬНАЯ РАБОТА №2
Задача №1. Найти неопределенные интегралы. Результаты проверить дифференцированием
| а) | б) | в) | |
| 1. | 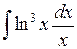
| 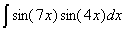
| 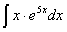
|
| 2. | 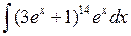
| 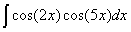
| 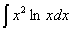
|
| 3. | 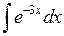
| 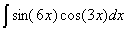
| 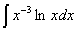
|
| 4. | 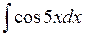
| 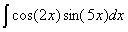
| 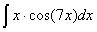
|
| 5. | 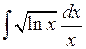
| 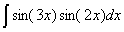
| 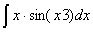
|
| 6. | 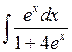
| 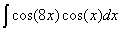
| 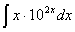
|
| 7. | 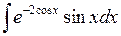
| 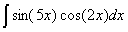
| 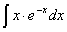
|
| 8. | 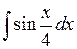
| 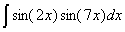
| 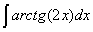
|
| 9. | 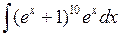
| 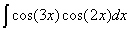
| 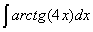
|
| 10. | 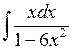
| 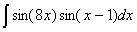
| 
|
| 11. | 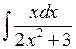
| 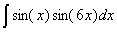
| 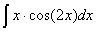
|
| 12. | 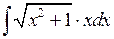
| 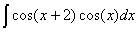
| 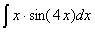
|
| 13. | 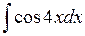
| 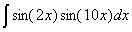
| 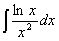
|
| 14. | 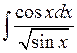
| 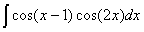
| 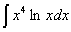
|
| 15. | 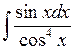
| 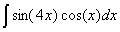
| 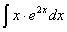
|
| 16. | 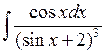
| 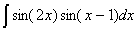
| 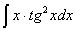
|
| 17. | 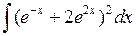
| 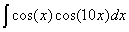
| 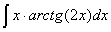
|
| 18. | 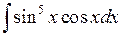
| 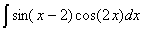
| 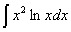
|
| 19. | 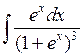
| 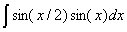
| 
|
| 20. | 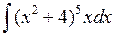
| 
| 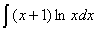
|
| 21. | 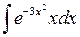
| 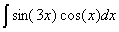
| 
|
| 22. | 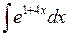
| 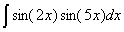
| 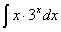
|
| 23. | 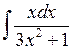
| 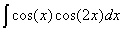
| 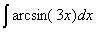
|
| 24. | 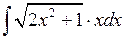
| 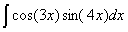
| 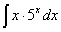
|
| 25. | 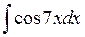
| 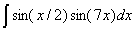
| 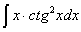
|
| 26. | 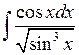
| 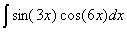
| 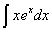
|
| 27. | 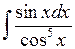
| 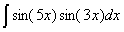
| 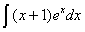
|
| 28. | 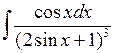
| 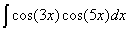
| 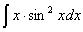
|
| 29. | 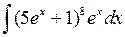
| 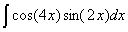
| 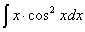
|
| 30. | 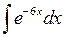
| 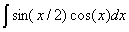
| 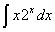
|
Задача №2. Вычислить определенный интеграл
| 1 | 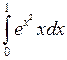
| 2 | 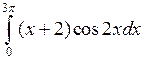
|
| 3 | 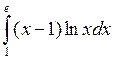
| 4 | 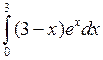
|
| 5 | 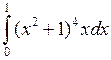
| 6 | 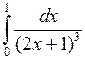
|
| 7 | 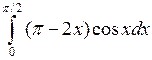
| 8 | 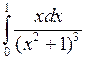
|
| 9 | 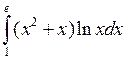
| 10 | 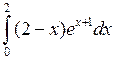
|
| 11 | 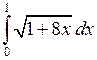
| 12 | 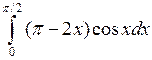
|
| 13 | 
| 14 | 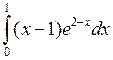
|
| 15 | 
| 16 | 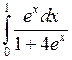
|
| 17 | 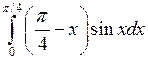
| 18 | 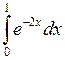
|
| 19 | 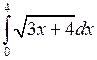
| 20 | 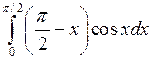
|
| 21 | 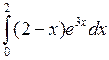
| 22 | 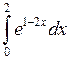
|
| 23 | 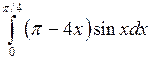
| 24 | 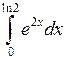
|
| 25 | 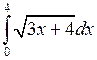
| 26 | 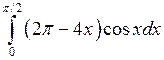
|
| 27 | 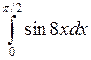
| 28 | 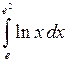
|
| 29 | 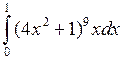
| 30 | 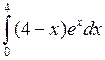
|
Задача №3. Найти площадь фигуры, ограниченной кривой
y = ax2 + px + q и прямой y = kx + b:
| 1. | y = x2 - 4x + 3 | y = -x + 1 |
| 2. | y = -x2 +2x + 2 | y = -x -2 |
| 3. | y = x2 - 3 | y = x - 1 |
| 4. | y = -x2 - 6x + 7 | y = -x - 1 |
| 5. | y = x2 - 3x + 1 | y = x - 2 |
| 6. | y = -x2 - 2x | y = x + 2 |
| 7. | y = x2 -3x | y = -x + 3 |
| 8. | y = -x2 - 2x - 1 | y = -x - 3 |
| 9. | y = x2 + 5x +6 | y = x + 3 |
| 10. | y = -x2 + 6x + 3 | y = x - 3 |
| 11. | y = x2 + x + 1 | y = -x +4 |
| 12. | y = -x2 - 4x | y = -x - 4 |
| 13. | y = x2 -2x + 3 | y = x + 1 |
| 14. | y = -x2 - x + 2 | y = x - 1 |
| 15. | y = x2 - 6x + 7 | y = -x + 1 |
| 16. | y = -x2 - 5x -4 | y = -x - 1 |
| 17. | y = x2 + 2x + 2 | y = x + 4 |
| 18. | y = -x2 + 3x - 1 | y = x - 4 |
| 19. | y = x2 + 2x + 6 | y = -x + 4 |
| 20. | y = -x2 + 3x - 7 | y = -x - 4 |
| 21. | y = x2 + 6x + 8 | y = x + 2 |
| 22. | y = -x2 + 2x | y = x - 2 |
| 23. | y = x2 - 4x - 2 | y = -x + 2 |
| 24. | y = -x2 + 2x - 4 | y = -x - 2 |
| 25. | y = x2 + 4x + 7 | y = x - 2 |
| 26. | y = x2 - 3x + 6 | y = x + 7 |
| 27. | y = -x2 - 2x + 3 | y = -x + 1 |
| 28. | y = x2 + x - 1 | y = x + 1 |
| 29. | y = -x2 - x + 1 | y = -x - 1 |
| 30. | y = x2 + 5x + 6 | y = x + 8 |
Задача №4. Вычислить частные производные 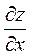 ,
, 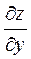
| Вариант | Функция |
| 1. | 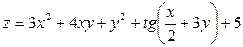
|
| 2. | 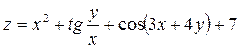
|
| 3. | 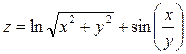
|
| 4. | 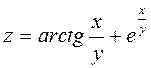
|
| 5. | 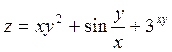
|
| 6. | 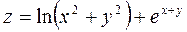
|
| 7. | 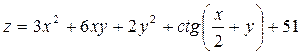
|
| 8. | 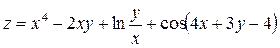
|
| 9. | 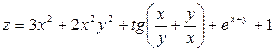
|
| 10. | 
|
| 11. | 
|
| 12. | 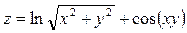
|
| 13. | 
|
| 14. | 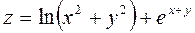
|
| 15. | 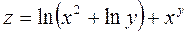
|
| 16. | 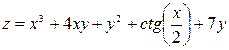
|
| 17. | 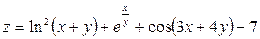
|
| 18. | 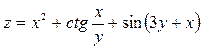
|
| 19. | 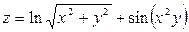
|
| 20. | 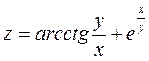
|
| 21. | 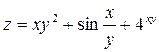
|
| 22. | 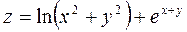
|
| 23. | 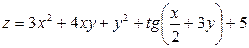
|
| 24. | 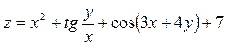
|
| 25. | 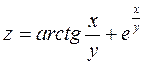
|
| 26. | 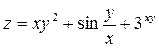
|
| 27. | 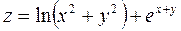
|
| 28. | 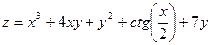
|
| 29. | 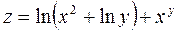
|
| 30. | 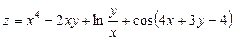
|
Задача №5. Найти общее решение дифференциального уравнения
a(x)y ¢ + b(x)y = f(x) и частное решение, удовлетворяющее начальному условию y = y0 при x = x0
| 1. | 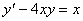
| y0 = 3/4 | x0 = 0 |
| 2. | 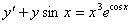
| y0 = 2 | x0 = 0 |
| 3. | 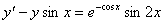
| y0 = 3 | x0 = 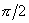
|
| 4. | 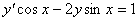
| y0 = -3 | x0 = 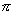
|
| 5. | 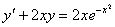
| y0 = 5 | x0 = 0 |
| 6. | 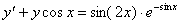
| y0 = 0 | x0 = 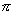
|
| 7. | 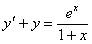
| y0 = 2 | x0 = 0 |
| 8. | 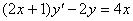
| y0 = 3 | x0 = 0 |
| 9. | 
| y0 = 2 | x0 = 1 |
| 10. | 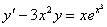
| y0 = 2 | x0 = 1 |
| 11. | 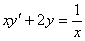
| y0 = 1 | x0 = 3 |
| 12. | 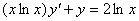
| y0 = 0 | x0 = e |
| 13. | 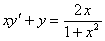
| y0 = 0 | x0 = 1 |
| 14. | 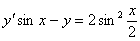
| y0 = 0 | x0 = 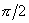
|
| 15. | 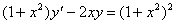
| y0 = 5 | x0 = -2 |
| 16. | 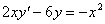
| y0 = 0 | x0 = 0 |
| 17. | 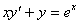
| y0 = 2 | x0 = 1 |
| 18. | 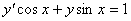
| y0 = 2 | x0 = 0 |
| 19. | 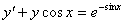
| y0 = 0 | x0 = 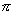
|
| 20. | 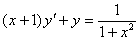
| y0 = 10 | x0 = 0 |
| 21. | 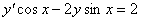
| y0 = 3 | x0 = 0 |
| 22. | 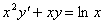
| y0 = 1 | x0 = 1 |
| 23. | 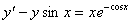
| y0 = 2 | x0 = 0 |
| 24. | 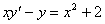
| y0 = 2 | x0 = 2 |
| 25. | 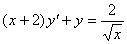
| y0 = 3 | x0 = 4 |
| 26. | 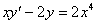
| y0 = 0 | x0 = 1 |
| 27. | 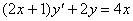
| y0 = 1 | x0 = 0 |
| 28. | 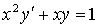
| y0 = 1 | x0 = 1 |
| 29. | 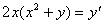
| y0 = 0 | x0 = 0 |
| 30. | 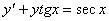
| y0 = 1 | x0 = 0 |
Дата: 2018-12-28, просмотров: 311.