Множества натуральных чисел
Чтобы множество Q+ положительных рациональных чисел являюсь расширением множества N натуральных чисел, необходимо выполнение ряда условий.
Первое условие - это существование между N и Q+ отношения включения. Докажем, что
N Ì Q+.
Пусть длина отрезка х при единичном отрезке е выражается натуральным числом m. Разобьем единичный отрезок на п равных частей. Тогда n-ая часть единичного отрезка будет укладываться в отрезке Х точно mп раз, т.е. длина отрезка х будет выражена дробью 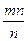 . Значит, длина отрезка х выражается и натуральным числом m, и положительным рациональным числом
. Значит, длина отрезка х выражается и натуральным числом m, и положительным рациональным числом 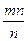 . Но это
. Но это
должно п быть одно и то же число. Поэтому целесообразно считать, что дроби вида 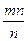 являются записями натурального числа m.
являются записями натурального числа m.
Следовательно, N Ì Q+.
Так, например, натуральное число 6 можно представить в виде следующих дробей: 6/1 12/2, 18/3 24/4, 30/5 и т.д.
Отношение между множествами N и Q+ представлено на рисунке 129.

Рисунок 129.
Числа, которые дополняют множество натуральных чисел до множества положительных рациональных, называются дробными.
Второе условие, которое должно быть выполнено при расширении множества натуральных чисел, - это согласованность операций, т.е. результаты арифметических действий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но выполненных по правилам, сформулированным для положительных рациональных чисел. Нетрудно убедиться в том, что и это условие выполняется.
Пусть а и b - натуральные числа, а + b - их сумма, полученная по правилам сложения в N. Вычислим сумму чисел а и b по правилу сложения в Q+. Так как а = 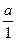 , b =
, b = 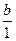 , то
, то 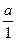 +
+ 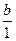 =
= 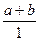 = а + b Убедиться в том, что второе условие выполняется и для других операций, можно аналогично.
= а + b Убедиться в том, что второе условие выполняется и для других операций, можно аналогично.
Третье условие, которое должно быть выполнено при расширении множества натуральных чисел - это выполнимость в Q+ операции, не всегда осуществимой в N. И это условие соблюдено: деление, которое не всегда выполняется в множестве N, в множестве Q+ выполняется всегда.
Сделаем еще несколько дополнений, раскрывающих взаимосвязи между натуральными и положительными рациональными числами.
1. Черту в записи дроби 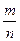 — можно рассматривать как знак деления.
— можно рассматривать как знак деления.
Действительно, возьмем два натуральных числа m и n и найдем их частное по правилу (4) деления положительных рациональных чисел:
m : n = 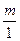 :
: 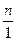 =
= 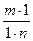 =
= 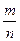 .
.
Обратно, если дана дробь 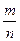 , то ее можно рассматривать как частое натуральных чисел m и n:
, то ее можно рассматривать как частое натуральных чисел m и n:
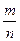 =
= 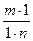 =
= 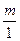 :
: 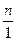 = m : n.
= m : n.
2. Любую неправильную дробь можно представить либо в виде натурального числа, либо в виде смешанной дроби.
Пусть 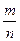 - неправильная дробь. Тогда m > n . Если m кратно n, то в этом случае дробь
- неправильная дробь. Тогда m > n . Если m кратно n, то в этом случае дробь 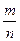 является записью натурального числа. Если число m не кратно n, то разделим m на n с остатком:
является записью натурального числа. Если число m не кратно n, то разделим m на n с остатком:
m = nq + r, где r < n.
Подставим nq + r вместо m в запись 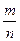 и применим правило (1) сложения положительных рациональных чисел:
и применим правило (1) сложения положительных рациональных чисел: 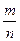 =
= 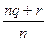 =
= 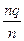 +
+ 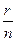 = q +
= q + 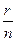 .
.
Так как r < n, то дробь 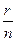 - правильная. Следовательно, неправильная дробь — оказалась представленной в виде суммы натурального числа q и правильной дроби
- правильная. Следовательно, неправильная дробь — оказалась представленной в виде суммы натурального числа q и правильной дроби 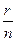 . Это действие называется
. Это действие называется
выделением целой части из неправильной дроби. Например, 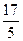 =
= 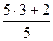 =
= 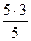 +
+ 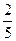 =3+
=3+ 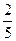 .
.
Сумму натурального числа и правильной дроби принято записывать без знака сложения: т.е. вместо
3 + 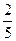 пишут 3
пишут 3 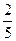 и называют такую запись смешанной дробью.
и называют такую запись смешанной дробью.
Справедливо также утверждение: всякую смешанную дробь можно записать в виде неправильной дроби. Например:
3 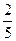 =3+
=3+ 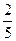 =
= 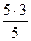 +
+ 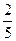 =
= 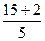 =
= 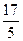 .
.
Упражнения
1. Какие из данных чисел являются дробными:
а) 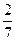 ; б)
; б) 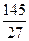 ; в)
; в) 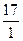 ; г)
; г) 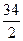 ?
?
7 27 1 2
2. Докажите, что вычитание, умножение и деление натуральных
чисел в множестве N и Q+ согласованно.
3.Число 2 умножили на правильную дробь. Какое число получилось - больше или меньше числа 2? А если 2 умножить на неправильную дробь?
4. Может ли при умножении числа 3 на правильную дробь получиться число:
а) меньше 1; б) больше 1?
5. Решите арифметическим методом задачи.
а) В трех гаражах помещается 460 машин. Число машин в первом гараже составляет 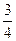 числа машин, помещающихся во втором, а в третьем гараже в 1
числа машин, помещающихся во втором, а в третьем гараже в 1 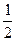 раза больше машин, чем в первом. Сколько машин в каждом гараже?
раза больше машин, чем в первом. Сколько машин в каждом гараже?
б) Из двух пунктов, расстояние между которыми 25 км, вышли одновременно навстречу друг другу два пешехода. Один из них проходил в час на 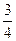 км больше другого. С какой скоростью шел каждый,
км больше другого. С какой скоростью шел каждый,
если через 2 ч после выхода расстояние между ними стало 7 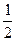 км?
км?
Лекция 50. Десятичные дроби
План:
1. Десятичные дроби. Алгоритмы арифметических действий над ними.
2. Преобразование обыкновенных дробей в десятичные.
3. Рациональные числа как бесконечные десятичные периодические дроби.
4. Преобразование периодических десятичных дробей в обыкновенные.
Дата: 2019-02-02, просмотров: 709.