В условиях термодинамического равновесия число генерируемых и рекомбинирующих в единицу времени носителей заряда в полупроводнике статистически одинаково, а полупроводник имеет некоторые равновесные концентрации свободных электронов и дырок, определяемые температурой и концентрацией примесей.

       Если полупроводник поглощает дополнительную энергию (например, при освещении), то концентрация носителей заряда может превысить равновесную. При снятии воздействия концентрация носителей заряда стремится к равновесной. Она устанавливается не мгновенно – спад идёт по экспоненциальному закону. Экспериментально установлено, что скорость рекомбинации носителей заряда пропорциональна избыточной концентрации и коэффициенту 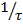, и представляющему собой существующую вероятность рекомбинации рассматриваемого носителя заряда (дырки) за одну секунду, т.е.

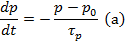
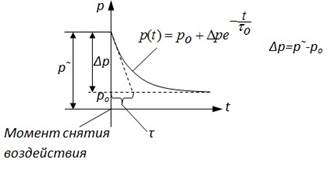
Решением уравнения (а) является экспоненциальная функция при начальных условиях

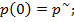
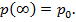
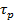 называют средним временем жизни избыточных носителей заряда.

Рекомбинация идёт как в объёме, так и на поверхности полупроводника, причём с разной скоростью. Как правило, стремятся уменьшить скорость поверхностной рекомбинации. Совместный учёт объёмной и поверхностной рекомбинации осуществляется с помощью соотношения:

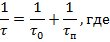
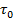 - среднее время жизни неравновесных носителей заряда в объёме полупроводника,  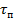- среднее время жизни неравновесных носителей заряда на поверхности полупроводника.

       Если воздействие локальное, то возникает диффузионное перемещение носителей заряда в сторону с их меньшей концентрацией. Причём концентрация неравновесных носителей заряда будет убывать в пространстве тоже по экспоненциальному закону

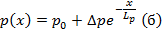
За среднее время жизни 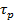 носители заряда перемещаются на диффузионную длину  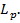Между диффузионной длиной  и средним временем жизни имеется следующая связь:

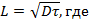
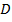   – коэффициент диффузии.

Дифференциальное уравнение (а) справедливо, если спад концентрации определяется только рекомбинацией, но не вытеснением носителей заряда из рассматриваемого элементарного объёма, т.е. (а) справедливо, если плотность тока 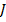 вдоль оси  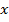постоянна. С учётом спада концентрации вдоль оси 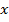, дифференциальное уравнение (а) принимает вид:

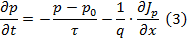
- уравнение непрерывности для одномерного случая.

Уравнения непрерывности (3), плотности тока (2) и распределения Ферми (1) являются основными уравнениями, на которых основывается теория полупроводниковых приборов.