Все переменные программы соответствуют переменным, которые введены в схеме алгоритма. Дополнительно определим их типы.
n — параметр ряда; по условиям задачи это — целое число; поскольку заранее неизвестно, сколько итераций цикла будет нужно для достижения предела точности, объявим его как "длинное целое":
long n;
Отметим, что хотя по условию задания n — целое, результаты выражений, в которых фигурирует n, будут иметь дробную часть. Преобразование типов можно выполнять непосредственно при вычислении выражения, но чтобы заранее исключить ошибки, введем еще одну переменную— dbln, которая будет представлять значение n как числа с плавающей точкой:
double dbln;
term — значение текущего члена ряда. Объявим его как:
double term;
sum — текущее значение суммы ряда с начальным значением 0. Объявим его как:
double sum=0;
k2 — переменная для сохранения текущего значения 2n с начальным значением 1 (см. пп.1.2). Она должна быть "длинным целым" — из тех же соображений, что и n:
long k2=1;
k1 — переменная для сохранения текущего значения (–1)n с начальным значением 1 (см. пп.1.3). Для нее достаточно быть "коротким целым":
short k1=1;
eps — переменная для представления заданного предела точности. Она должна иметь начальное (неизменное) значение 0.000001, поэтому может быть объявлена как const. Использование переменной для представления константы вместо употребления константы непосредственно в операторах программы может повысить гибкость программы:
const double eps=0.000001;
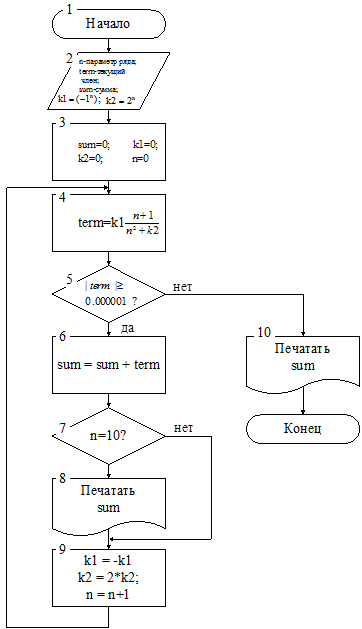
Рисунок 2.4 — Блок-схема алгоритма решения задачи
Разработка текста программы
Начинаем разработку текста программы с заголовка главной функции main():
int main(void)
Далее открывается тело функции, и в него включаются определения переменных (см. п.2). Определения переменных реализуют блок 2 блок-схемы алгоритма. В дополнение к переменным, определенным в схеме алгоритма, объявляем рабочую переменную dbln и константу eps. Поскольку правила языка C позволяют присваивать переменным начальные значения, в объявлении переменных отчасти реализован также и блок 3. Блоки 4–9 схемы алгоритма образуют цикл. В языке C есть два "простых" оператора цикла: цикл с предусловием — whіle и цикл с постусловием — do-whіle. Но по схеме алгоритма видно, что выход из цикла происходит в середине тела цикла (блок 5): после вычисления члена ряда, но до добавления его значения к сумме. Следовательно, "простые" циклы применить нельзя. "Сложный" оператор цикла— for — является циклом с предусловием, но задавать условие в самом операторе цикла необязательно. К тому же этот оператор дает возможность определить действия, которые нужно выполнить до начала цикла и действия, которые выполняются в конце каждой итерации. Таким образом, открытие цикла будет иметь вид:
for (n=0; ; n++, k2*=2, k1=-k1) {
где первый параметр for — присваивание начального значения переменной n (остаток блока 3), второй параметр — условие выхода из цикла — пустой, третий параметр реализует блок 8 схемы алгоритма. В теле цикла содержится несколько отдельных действий, значит, будет несколько операторов, поэтому тело цикла берется в операторные скобки.
В теле цикла первый оператор: dbln=n;
это действие не предусмотрено в схеме алгоритма, но его необходимость пояснили в п.2.
Далее вычисляется значение текущего члена ряда:
term=k1*(dbln+1)/(dbln*dbln+k2);
этот оператор полностью реализует блок 4 и формулу из индивидуального задания (учитывая пп.1.2, 1.3) за исключением того, что вместо операции возведения в степень 2 применяем умножение.
Следующее действие — проверка достижения предела точности — на схеме алгоритма представлена блоком 5 и выполняется условным оператором, который начинается с:
if (fabs(term)>=eps)
Следует отметить, что сравнивается абсолютное значение term, а функция для получения абсолютного значения переменной типа double — fabs(). Эта функция описана в файле math.h, так что нужно включить этот файл в начало программы:
#іnclude <math.h>
Продолжение условного оператора, действие, которое выполняется при выполнении условия, — добавление значения члена к сумме (блок 6):
sum+=term;
При невыполнении условия нужно выйти из цикла, так что условный оператор требует и второй части:
else break;
По схеме алгоритма надо проверить, не достигла ли переменная n значения 9 (блок 7), и, если да, — печатать значение суммы (блок 8). Это реализуется условным оператором:
if (n==9) printf("Сумма 10 членов ряда=%10.7lf\n",sum);
Поскольку при невыполнении условия не делается ничего, часть else для этого оператора не нужна.
При вызове функции всегда возникает проблема форматизации вывода. включили в формат текст, который поясняет вывод, а значение переменной sum выводим по спецификации %10.7lf. Тип спецификации соответствует типу переменной — double, а числовые параметры выбрали произвольно, поскольку в задании не оговорены требования к точности вывода. Перед точкой оставляем 2 позиции — для знака и целой части (которая должна быть 0), после точки — 7 позиций, что на 1 превышает точность заданного предела точности. Функция prіntf() описана в файле stdіo.h, поэтому включаем этот файл в начало программы:
#include <stdio.h>
Поскольку блок 9 схеми алгоритма реализован нами в заголовке цикла, то цикл на этом заканчивается, и ставим операторную скобку, закрывающую тело цикла.
Выход из цикла происходит по оператору break в составе условного оператора. После выхода из цикла должны напечатать окончательное значение суммы (блок 10), что и делаем оператором:
prіntf("Повна сума ряду = %10.7lf\n",sum);
При определении формата вывода работают те же соображения, что и в предыдущем случае. Реализация алгоритма закончена, ставим операторную скобку, которая закрывает тело функции maіn().
Полный текст программы приведен ниже.
#include <stdio.h> #include <math.h> int main(void) { longn; /* параметр ряда */ double dbln; /* параметр рядав форме с плавающей точокй */ double sum=0; /* сумма членов ряда */ double term; /* значениетекущего члена */ constdouble eps=0.000001; /* пределточности */ long k2=1; /* pow(2,n)*/ short k1=1; /* pow(-1,n)*/ /* основной цикл; в модификациях вычисляются следующие значения pow(2,n) и pow(-1,n)*/ for (n=0; ; n++, k2*=2, k1=-k1) { /* преобразование n в форму с плавающей точкой */ dbln=n; /* вычисление очередного члена */ term=k1*(dbln+1)/(dbln*dbln+k2); /* проверка достижения предела точности */ if (fabs(term)>=eps) /* если не достигнут - накопление суммы */ sum+=term; /* если досягнут - выход из цикла */ else break; /* если 10 членов - вывод суммы */ if (n==9) printf("Сумма 10 членовряда = %10.7lf\n",sum); } /* конец основного цикла */ /* вывод окончательной суммы */ printf("Полная сумма ряда = %10.7lf\n",sum); return 0; }Отладка программы
При отладке программы целесообразно использовать пошаговый режим с отслеживанием значений переменных — прежде всего: n, term, sum. Следует выполнить шаг за шагом несколько итераций цикла, убеждаясь, что эти переменные получают правильные значения. В таком режиме нетрудно выполнить 10 итераций и убедиться в правильном формировании первого результата. Если возникают ошибки при вычислении наиболее сложного выражения в программе:
term=k1*(dbln+1)/(dbln*dbln+k2);
можно включить в программу временные дополнительные переменные и разбить выражение на простые составляющие, проверяя на шаг за шагом значения этих переменных. Например:
double temp1, temp2; /* временные переменные */ . . . temp1=dbln+1; temp2=dbln*dbln; temp2=temp2+k2; temp1=temp1/temp2; term=k1*temp1;Для того, чтобы убедиться в правильном выводе второго результата, имеет смысл при отладке выводить вместе с суммой и номер итерации, на котором закончилась робота цикла, и значение члена ряда, которое оказалось меньше предела точности:
printf("%ld %10.7lf\n",n,term);
ЛАБОРАТОРНАЯ РАБОТА №8
Циклы с постусловием и предусловием
Цель работы : получение практических навыков в работе с операторами цикла языка C с использованием пост- и предусловия.
Темы для предварительной проработки
· Операторы цикла языка С
· Условный оператор
Задание: Разработать блок-схему алгоритма и программу на языке Си для вычисления значений функций на всем диапазоне изменения аргумента с заданным шагом. Исходные данные и функции представлены в таблице 2.10. Предусмотрите ввод всех исходных данных с клавиатуры.
Методические указания .
При составлении блок-схемы следует помнить, что алгоритм должен работать для любых удовлетворительных начальных данных.
В ходе решения задачи следует предусмотреть ввод исходных данных с клавиатуры (задать именованные переменные для начального, конечного значения переменной и шага) для создания программы, работающей с любыми числовыми данными. Если значения функции невозможно вычислить из-за невозможности деления на ноль или через другую аномальную ситуацию, необходимо вывести соответствующее сообщение.
При составлении блок-схемы и программы необходимо использовать механизмы цикла с предусловием или цикла с постусловием согласно варианту задания.
Номер варианта устанавливается преподавателем, который проводит руководство лабораторными занятиями (см. таблицы, распределенные в группах лектором, относящиеся к общим рекомендациям соответственно). Данные для вариантов представлены в таблице 2.10.
Таблица 2.10 — Варианты заданий для вычисления значений функций при изменении значений аргумента от начального значения до конечного с некоторым шагом
| № вар | Математическая модель решаемой задачи | Входные и выходные данные (ввод всех входных данных производится с клавиатуры) |
| 1 | 2 | 3 |
| 1 |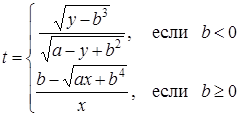 
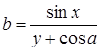
| Задано: a=1.8; x=–3.87; 1£y£3; Dy=0.1 Вывести: b, y, t; S=åt, если t£0; P=Õb, если b>0; F=(S+P)×a Постусловие |
| 2 |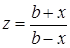 
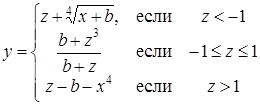
| Задано: b=5.8; –3£x£3; Dx=0.5 Вывести: x, y, z; n — количество z>0; P=Õy, если y³0; S=åy, если y<0 Предусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 3 |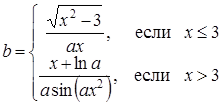 
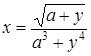
| Задано:
a=1.28;
2£y£5; Dy=0.3
Вывести: x, y, b;
k — количество b<x;
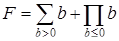Постусловие
|
| 4 |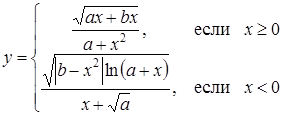 
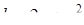
| Задано: a=2.17; –1.5£x£0.5; Dx=0.1 Вывести: x, y, b; k — количество y³0; P=Õy, если y³0; S=åy Предусловие |
| 5 |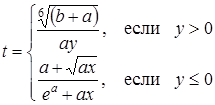 
 ; 
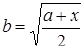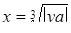
| Задано: a=1.8; –1£y£3; Dy=0.2 Вывести: x, b, y, t; n — количество t>0; S=åt, если t£0; P=Õt, если t>0 Постусловие |
| 6 |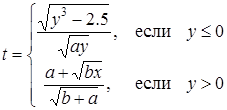 
 ;
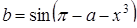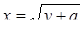
| Задано: a=1.8; 1£y£3; Dy=0.1 Вывести: x, b, y, t; S=åt, если t£0; P=Õt, если t>0; Q=(P–S)×a Предусловие |
| 7 |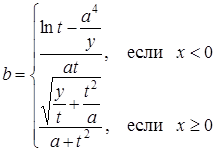 
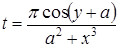
| Задано: a=4.8; x=6; 1£y£3; Dy=0.1 Вывести: b, y, t; S=åt, если t£0; P=Õb, если b>0; k — количество t£0 Постусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 8 |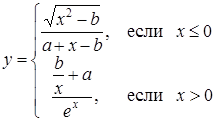 
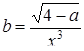
| Задано: a=1.28; –3£x£5; Dx=0.4 Вывести: x, y, b; k — количество y>0; F=Õy–åb Предусловие |
| 9 |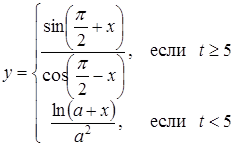 
| Задано: a=5.8; –3£x£3; Dx=0.5 Вывести: x, y, t; k — количество y<0; P=Õt, если t³0; S=åt, если t³0 Постусловие |
| 10 |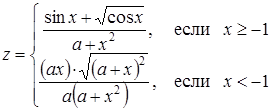 
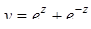
| Задано: a=5.8; –3£x£3; Dx=0.5 Вывести: x, z, y; k — количество y>20; P=Õz, если z³0; S=åz, если z<0 Предусловие |
| 11 |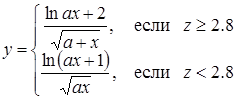 
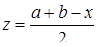
| Задано: a=16.7; b=–8.9; 2£x£3; Dx=0.1 Вывести: x, y, z; k — количество y<0.3; P=Õy; S=åy Постусловие |
| 12 |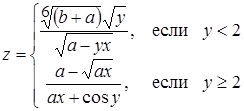 
 ; 
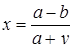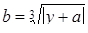
| Задано: a=3.15; 1£y£3; Dy=0.1 Вывести: x, b, y, z; S=åz, если z£0; P=Õz, если z>0; G=P–S Предусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 13 |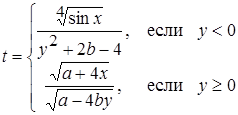 
 ; 
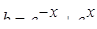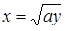
| Задано: a=2.1; 2£y£8; Dy=0.5 Вывести: x, b, y, t; S=åt, если t£10; F=Õt, если t>0; D=P–S Постусловие |
| 14 |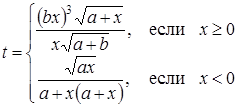 
| Задано: a=1.52; –4£x£4; Dx=0.5 Вывести: x, b, t; k — количество t<0; P=Õt, если t<0; S=åt, если t³0 Предусловие |
| 15 |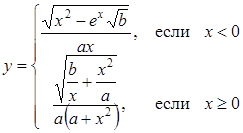 
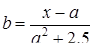
| Задано: a=1.28; –2£x£4; Dx=0.6 Вывести: x, y, b; k — количество y>2; F=Õy–åy Постусловие |
| 16 |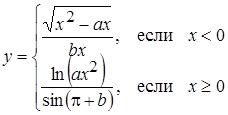 
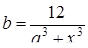
| Задано: a=3.15; –4£x£4; Dx=0.5 Вывести: x, y, b; k — количество y<0; F=Õy–åy Предусловие |
| 17 |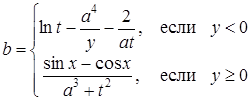 
 ; 
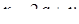
| Задано: a=–2.8; –1£y£3; Dy=0.4 Вывести: b, y, x, t; S=åt, если t£0; P=Õt, если t>0; G=(P+S)×a Постусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 18 |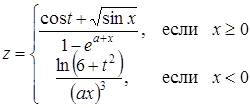 
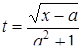
| Задано: a=7.8; –3£x£3; Dx=0.5 Вывести: x, z, t; k — количество z<0; P=Õz, если z³0; S=åz, если z<0 Предусловие |
| 19 |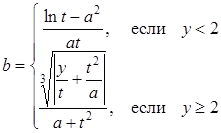 
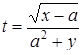
| Задано: a=4.8; x=6; 1£y£3; Dy=0.1 Вывести: b, y, t; S=åt, если t£10; P=Õb, если b>0; G=S–P Постусловие |
| 20 |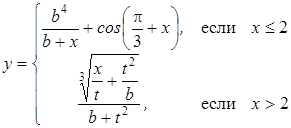 
 ; 
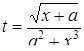
| Задано: a=4.8; 1£x£3; Dx=0.1 Вывести: b, y, t, x; S=åt, если t£0; P=Õy, если y>0; F=P+S Предусловие |
| 21 |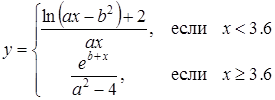 
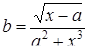
| Задано: a=1.28; 2£x£5; Dx=0.2 Вывести: x, y, b; k — количество y³10; F=Õy–åy Постусловие |
| 22 |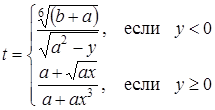 
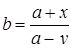
| Задано: a=1.8; x=–2.14; –1£y£3; Dy=0.2 Вывести: b, y, t; S=åt, если t£0; P=Õt, если t>0; G=S–P Предусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 23 |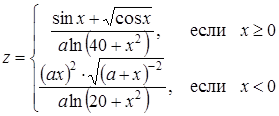 
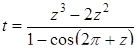
| Задано: a=5.8; –3£x£3; Dx=0.5 Вывести: x, z, t; m — количество t<0; P=Õz, если z³0; S=åz, если z<0 Постусловие |
| 24 |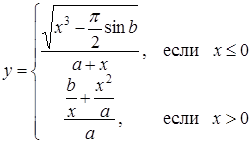 
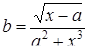
| Задано: a=1.28; 2£x£5; Dx=0.4 Вывести: x, y, b; n — количество y>b; F=Õy–åy Предусловие |
| 25 |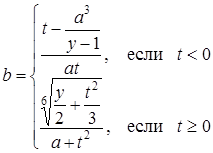 
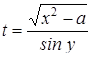
| Задано: a=4.8; x=6; 1£y£3; Dy=0.1 Вывести: b, y, t; S=åt, если t£0; P=Õb, если b<0; G=P–S Постусловие |
| 26 |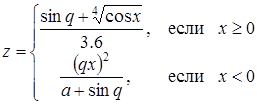 
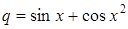
| Задано: a=5.8; –3£x£3; Dx=0.5 Вывести: x, z, q; k — количество z<0; F=Õz, если z³0; S=åz, если z<0 Предусловие |
| 27 |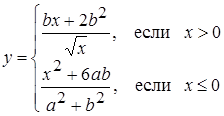 
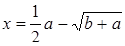
| Задано: a=6.4; 1.2£b£6; Db=0.2 Вывести: b, x, y; k — количество y>0; S=åy, если y<10 Постусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 28 |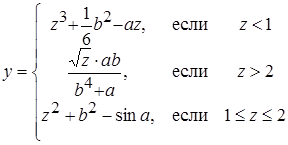 
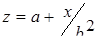
| Задано: a=0.3; b=1.8; 0£x£10; Dx=0.5 Вывести: x, z, y; k — количество z>2; P=Õz, если z<1 Предтусловие |
| 29 |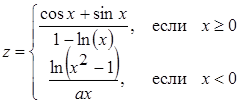 
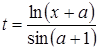
| Задано: a=2.2; –3£x£3; Dx=0.5 Вывести: x, z; k — количество z<0; P=Õz, если z<0; S=åz, если z³0 Постусловие |
| 30 |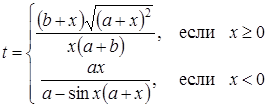 
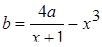
| Задано: a=2.3; –2£x£2; Dx=0.2 Вывести: x, b, t; k — количество t³0; P=Õt, если t³0; S=åt, если t<0 Предтусловие |
| 31 |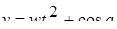 
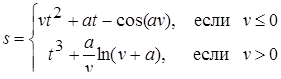
| Задано: a=0.3; w=3.6; 1£t£2; Dt=0.01 Вывести: t, v, s; X=ås, если s>0; P=Õs, если s£0 Постусловие |
| 32 |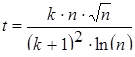 
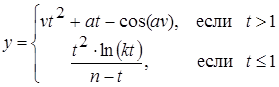
| Задано: k=3.02; 1£n£6; Dn=0.02 Вывести: n, t, y; S=åy, если y³0; P=Õy, если y<0 Предусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 33 |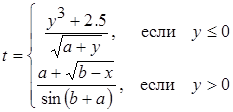 
 ;
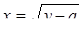
| Задано: a=2.3; –2£y£2; Dy=0.2 Вывести: x, b, y, t; S=åb, если b£0; P=Õt, если t>0; Постусловие |
| 34 |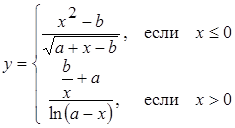 
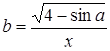
| Задано: a=4.1; –2£x£2; Dx=0.2 Вывести: x, y, b; k — количество b>0; F=Õy+åb Предусловие |
| 35 |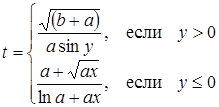 
 ; 
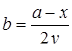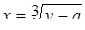
| Задано: a=2.8; –3£y£4; Dy=0.5 Вывести: x, b, y, t; n — количество t>2; S=åt, если t>0; P=Õt, если t£0 Постусловие |
| 36 |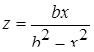 
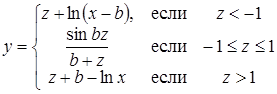
| Задано: b=–1.6; –2£x£4; Dx=0.5 Вывести: x, y, z; n — количество y>0; P=Õy, если z³0; S=åy, если z<0 Предусловие |
| 37 |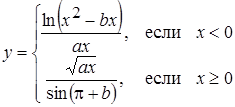 
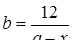
| Задано: a=1.5; –3£x£2; Dx=0.5 Вывести: x, y, b; k — количество y>0; F=Õy–åb Постусловие |
Таблица 2.10 — Продолжение
| 1 | 2 | 3 |
| 38 |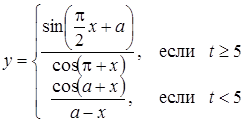 
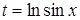
| Задано: a=1.4; –4£x£4; Dx=0.5 Вывести: x, y, t; k — количество t<0.5; P=Õt, если y<0; S=åt, если y³0 Предусловие |
| 39 |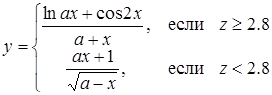 
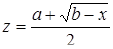
| Задано: a=3.7; b=–2.1; 2£x£3; Dx=0.1 Вывести: x, y, z; k — количество y<0.5; P=Õy; S=åz Постусловие |
| 40 |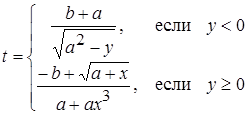 
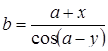
| Задано: a=–1.8; x=2.1; –2£y£3; Dy=0.5 Вывести: b, y, t; S=åt, если t>0; P=Õt, если t£0; Предусловие |
| 41 |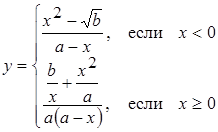 
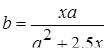
| Задано: a=2.8; –2£x£2; Dx=0.2 Вывести: x, y, b; k — количество y<2; F=Õb–åy Постусловие |
Примечание: здесь Õz, если z³0 — произведение всех неотрицательных значений z, åz, если z<0— сумма всех отрицательных значений z.
Примеры составления подобных блок-схем были рассмотрены ранее (см.рис.2.2)
Контрольные вопросы :
- Дать определение циклического вычислительного процесса и назвать виды циклов.
- Операторы цикла: приведите примеры их работы.
- Как работает цикл с предусловием?
- Как работает цикл с постусловием?
- Что такое цикл с известным количеством повторов?
ЛАБОРАТОРНАЯ РАБОТА №9
Работа с матрицами. Составление меню
Цель работы : получение практических навыков в работе с матрицами в языке C
Темы для предварительной проработки
· Операторы цикла языка C. Вложенные циклы.
· Условный оператор языка C.
· Матрицы
Задание: Создать квадратную матрицу целых чисел размером 9х9. В индивидуальных заданиях указано, какую обработку матрицы требуется выполнить.
Если по условию задания матрицу следует заполнить случайными числами, рекомендуем выбирать эти числа из диапазона 0 – 99. Если по условию задания в матрицу следует записать ЛП — линейную последовательность чисел, имеется в виду последовательность: 1, 2, 3, ... Программу разработатьсиспользованием меню!!!
Номер варианта устанавливается преподавателем, который проводит руководство лабораторными занятиями (см. таблицы, распределенные в группах лектором, относящиеся к общим рекомендациям соответственно). Данные для вариантов представлены в таблице 2.11.
Таблица 2.11 — Варианты индивидуальных заданий
| Вариант | Содержание задания | Иллюстрация |
| 1 | Заполнить матрицу ЛП, от левого верхнего угла по диагонали: влево — вниз. | 
|
| 2 | Заполнить секторы матрицы, которые лежат слева и справа от главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. |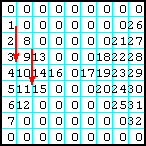 
|
| 3 | Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно побочной диагонали |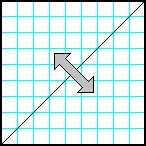 
|
| 4 | Заполнить матрицу случайными числами. Отобразить симметрично относительно вертикальной оси секторы матрицы, которые лежат слева и справа от главной и побочной диагоналей. |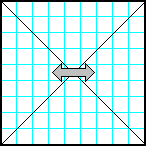 
|
| 5 | Заполнить матрицу случайными числами. Отобразить верхнюю половину матрицы на нижнюю зеркально симметрично, относительно горизонтальной оси. |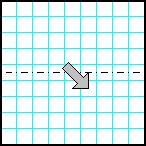 
|
| 6 | Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. | 
|
| 7 | Заполнить матрицу случайными числами. Отобразить главную и побочную диагонали симметрично относительно вертикальной оси. | 
|
| 8 | Заполнить матрицу случайными числами. Разместить на главной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к главной. |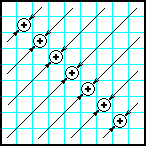 
|
| 9 | Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями. |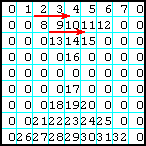 
|
| 10 | Заполнить матрицу случайными числами. Отобразить симметрично относительно горизонтальной оси секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей. |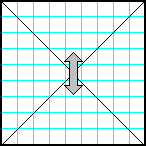 
|
| 11 | Заполнить матрицу случайными числами. Развернуть матрицу на 180o. | 
|
| 12 | Заполнить матрицу ЛП, от левого нижнего угла по диагонали: влево — вверх. | 
|
| 13 | Заполнить секторы матрицы, которые лежат слева и справа от главной и побочной диагоналей ЛП, от левого верхнего угла вправо — вниз. Остаток матрицы заполнить нулями. | 
|
| 14 | Заполнить матрицу ЛП, от левого верхнего угла по диагонали: вправо — вверх. | 
|
| 15 | Заполнить матрицу случайными числами. Отобразить главную и побочную диагонали симметрично относительно горизонтальной оси. |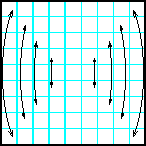 
|
| 16 | Заполнить матрицу ЛП, от правого верхнего угла по диагонали: влево — вниз. | 
|
| 17 | Заполнить матрицу случайными числами. Развернуть матрицу на 90o против часовой стрелки. |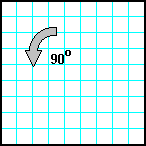 
|
| 18 | Заполнить матрицу случайными числами. На побочной диагонали разместить суммы элементов, которые лежат на той же строке и столбце. |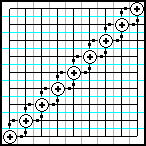 
|
| 19 | Заполнить матрицу случайными числами. На главной диагонали разместить суммы элементов, которые лежат на той же строке и том же столбце. |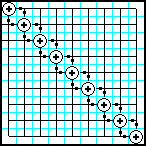 
|
| 20 | Заполнить матрицу случайными числами. Отобразить правую половину матрицы на левую зеркально симметрично относительно вертикальной оси. |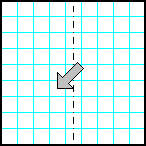 
|
| 21 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вниз — вправо — вверх — влево. | 
|
| 22 | Заполнить матрицу случайными числами. Отобразить левую половину матрицы на правую зеркально симметрично относительно вертикальной оси. |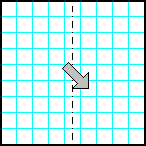 
|
| 23 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — влево — вверх — вправо. | 
|
| 24 | Заполнить матрицу случайными числами. Развернуть матрицу на 90o по часовой стрелке. |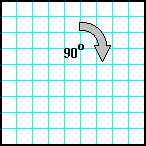 
|
| 25 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от центра по спирали: вниз — вправо — вверх — влево. |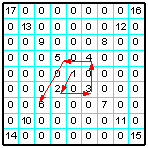 
|
| 26 | Заполнить матрицу случайными числами. Разбить матрицу на квадраты размером 3х3. В центре каждого квадрата поместить сумму остальных элементов квадрата. | 
|
| 27 | Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно главной диагонали |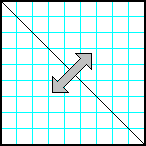 
|
| 28 | Заполнить матрицу нулями, после чего заполнить диагонали матрицы ЛП от левого верхнего угла по спирали: вправо — вниз — влево — вверх. |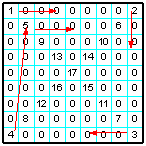 
|
| 29 | Заполнить матрицу случайными числами. Отобразить нижнюю половину матрицы на верхнюю зеркально симметрично относительно горизонтальной оси. |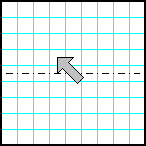 
|
| 30 | Заполнить матрицу случайными числами. Разместить на побочной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к побочной. |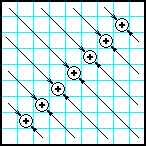 
|
| 31 | Заполнить нечетные диагонали, симметричные побочной, с левого верхнего угла заданным образом. Остаток матрицы заполнить нулями. | 
|
| 32 | Заполнить главную и побочные диагонали матрицы ЛП начиная с верхнего угла главной диагонали и останавливая заполнение в нижнем углу побочной диагонали (срединную точку заполнять один раз, если она есть). Остаток матрицы заполнить нулями. | 
|
| 33 | Заполнить матрицу из центра, распространяя ЛП в обе стороны параллельно строкам и столбцам. | 
|
| 34 | Заполнить матрицу ЛП по диагоналям, симметричным побочной, с левого верхнего угла заданным образом — на каждой из диагоналей числа одинаковые вдоль нее. | 
|
| 35 | Заполнить матрицу ЛП змейкой, начиная ее с левого верхнего угла матрицы вниз и заполняя ее на следующем столбце в обратном направлении. | 
|
| 36 | Заполнить матрицу случайными числами. Отобразить левые части главной и побочной диагоналей симметрично относительно вертикальной оси. |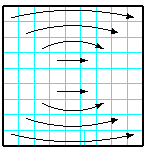 
|
| 37 | Заполнить матрицу ЛП змейкой, начиная ее с нижнего правого угла матрицы влево и заполняя ее на следующей строке в обратном направлении. | 
|
| 38 | Заполнить матрицу из центра, распространяя ЛП в обе стороны параллельно главной и побочной диагоналям. | 
|
| 39 | Заполнить матрицу случайными числами. На срединных строках и столбцах разместить суммы элементов, лежащих в соответствующих строках и столбцах. |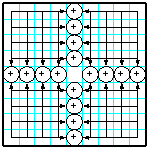 
|
| 40 | Заполнить нечетные диагонали, симметричные главной, с правого верхнего угла заданным образом. Остаток матрицы заполнить нулями. | 
|
Методические указания
Пример решения задачи
| Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз — вправо. Остаток матрицы заполнить нулями. | 
|
1. Разработка алгоритма решения
Обозначим размерность матрицы как S, номер строки как L, а номер столбца как R, и (имея в виду, что реализация алгоритма будет выполнена на языке С) примем, что нумерация строк и столбцов будет начинаться с 0. Отсюда можно определить, что в строке с номером L ненулевые элементы в верхней части матрицы лежат на столбцах с номерами R1=L<R<R2=S–L, а в нижней—R1=S–L–1<R<R2=L. Следовательно, алгоритм может состоять из перебора матрицы строка за строкой с определением для каждого элемента, удовлетворяют ли его индексы вышеприведенным условиям. Если да — элементу присваивается следующее значение из ЛП, если нет — 0.
Но можно несколько упростить алгоритм, обойдя вычисления граничных значений для каждого элемента и необходимости определения, в верхнюю или нижнюю часть матрицы ми попадаем. Обратим внимание на то, что для первой строки (L=0) R1=1, R2=S–2. Для каждой следующей строки R1 увеличивается на 1, а R2 уменьшается на 1. При пересечении середины матрицы, направление модификации изменяется на противоположное: теперь для каждой следующей строки значение R1 уменьшается на 1, а значение R2 - увеличивается на 1. Признаком пересечения середины может быть условие R1>R2, оно выполняется в момент пересечения. Схема алгоритма показана на рисунке 2.5.
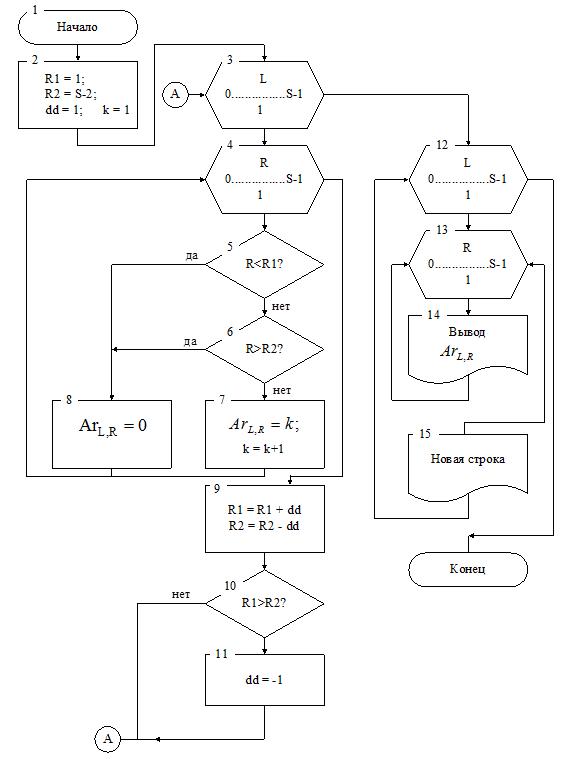
Рисунок 2.5 — Блок схема алгоритма программы
Вместе с описанными выше переменными R1 и R2, которые получают начальные значения для первой строки матрицы, мы вводим переменную dd с начальным значением 1 — это то значение, которое будет модифицировать R1 и R2 для каждой следующей строки, и переменную k— в которой будет значение текущего члена ЛП, начальное значение — 1 (блок 2). Далее организуются вложенные циклы. Во внешнем цикле перебираются строки (блок 3), а во внутреннем — столбцы матрицы (блок 4). В каждой итерации внутреннего цикла номер столбца R сравнивается с граничными значениями R1, R2 (блоки 5, 6). Если он лежит в пределах от R1 до R2, то текущему члену матрицы присваивается значение k— текущего члена ЛП, а потом k увеличивается на 1 (блок 7). Если нет, то текущему члену присваивается значения 0 (блок 8).
После выхода из внутреннего цикла модифицируются граничные значения:R1 увеличивается на dd, аR2 уменьшатся на dd (блок 9). Напомним, что начальное значение dd=1. Когда выполняется условие R1>R2(блок 10) присваиваем dd значение –1, далее модификация границ будет соответствовать правилам для нижней части матрицы.
После выхода из внешнего цикла, который начался в блоке 3, вновь организуются вложенные циклы перебора строк (блок 12) и столбцов (блок 13). В каждой итерации внутреннего цикла выводится значение одного элемента матрицы (блок 14), после выхода из внутреннего цикла начинается новая строка вывода (блок 15).
Дата: 2019-02-02, просмотров: 470.
