Такая группа принадлежит кривошнпно-шатунному ме­ханизму и состоит из шатуна 2, соединенного с ползуном 3 (рис. 1).

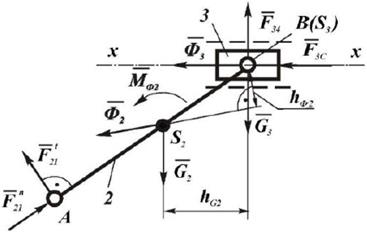
Рис. 1. Схема сил группы Ассура 2-3 (ВВП), μ _l =..., м/мм

Расчет начинаем с определения сил тяжести звеньев G ₂ и G ₃, которые приложены в их центрах тяжести S ₂ и S₃, направ­лены вертикально вниз и определяются как произведение мас­сы звена т, на ускорение свободного падения g = 9,81:

G_i = m_i ∙ g.

Так как группа освобождена от связей, то вместо них прикладываем соответствующие реакции: реакцию 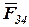, дей­ствующую в поступательной паре со стороны неподвижного звена 4 на звено 3, и реакцию 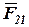, действующую в шарнире А со стороны звена 1 на звено 2.

Реакция 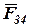 не известна по величине, но известна по направлению она перпендикулярна направляющей 4.

Реакция 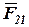 не известна ни по величине, ни по направ­лению. Раскладываем ее на две составляющие: тангенциаль­ную 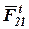, направленную перпендикулярно звену А B, и нор­мальную 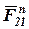, направленную вдоль звена А B.

Сила производственного сопротивления 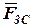 действует на ползун 3, проходит через его центр тяжести S ₃ совпадаю­щий с точкой B, направлена против движения ползуна (на­правление движения определяется по направлению скорости точки B, из плана скоростей для данного положения механиз­ма). Величина силы либо задана, либо определяется по инди­каторной диаграмме.

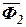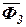Для того, чтобы рассматривать группу как находящуюся в равновесии, прикладываем в точках S ₂ и S₃ главные векторы сил инерции и . Величины этих сил определяем по формулам:

;   .

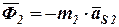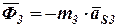Знак минус в этих формулах показывает, что главные векторы сил инерции направлены противоположно векторам ускорений центров тяжести звеньев.

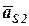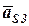Величины и направления ускорений центров тяжести звеньев  и определяем по плану ускорений для данно­го положения механизма.

К звену 2 прикладываем еще главный момент сил инер­ции:

.

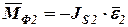Величину углового ускорения определяем следующим образом:

.

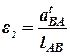Величину и направление 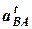 определяем по плану уско­рений. Направление ε ₂ совпадает с направлением .

Численное значение момента инерции J_{S 2} дано в задании или может быть определено по формуле:

.

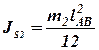Переходим к определению реакци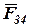й  и 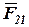 а также реакции 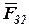действующей в шарнире В со стороны звена 2 па звено 3. Расчет производим в следующем порядке.

1. Рассматриваем равновесие звена 2 и определяем силу 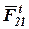. Так как звено 2 находится в равновесии, то сумма момен­тов всех сил, приложенных к этому звену, относительно точки В равна нулю:

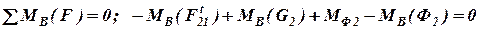
или     ,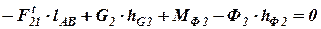

тогда

.

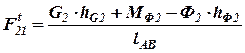В этом уравнении и далее плечи сил обозначены через h с индексами этих сил. Все плечи определяются непосредст­венным измерением на чертеже с учетом масштабною коэф­фициента μ _l .

Если сила 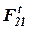 получится со знаком минус, то это значит, что она направлена противоположно тому направлению, ко­торое мы первоначально показали на чертеже и использовали при составлении уравнения. В дальнейших расчетах мы долж­ны будем принимать ее действительное направление.

2. Рассматриваем равновесие всей группы в целом и оп­ределяем реакци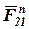и  и .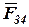

Так как группа находится в равновесии, то геометриче­ская сумма всех сил, действующих на ее звенья, равна нулю:

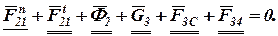
Двумя линиями подчеркнуты силы, известные по вели­чие и по направлению, одной линией - силы, у которых из­вестны только направления.

В соответствии с этим уравнением строим многоуголь­ник сил (план сил). Многоугольник должен быть замкнутым.

Для этого выбираем произвольно масштабный коэффи­циент сил [μ _F]=Н/мм и вычисляем длины векторов, которые будут изображать известные силы.

Чтобы получить длину вектора силы, нужно величину силы разделить на масштабный коэффициент.

Затем, начиная от точки 0 (рис.2), откладываем последо­вательно векторы известных сил. В конце каждого вектора делаем стрелку и ставим обозначение силы.

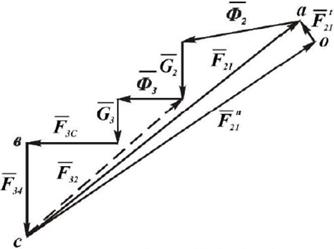
Рис. 2. План сил группы Ассура 2-3 (ВВП), μ _F =..., Н/мм

Построение известных сил заканчиваем вектором 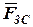в точке в. Чтобы замкнуть многоугольник, проводим через точ­ку 0 направление силы  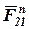а через точку в - направление си­лы 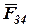. Эти силы пересекаются в точке с и замыкают силовой многоугольник. Точка пересечения этих сил определит их ве­личину: отрезок  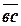изображает силу 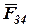, а отрезок  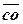– силу .

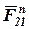Определяем их истинные величины.

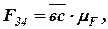
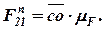
Определив 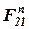 и 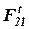, нужно на плане сил найти пол­ную реакцию F ₂₁ как их равнодействующую: проведем пря­мую из начала вектора  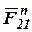(точка с) в конец вектора 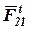_, это и будет полная реакция 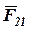, действующая в точке А. Разуме­ется .

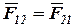3. Рассматриваем равновесие звена 3 и определяем реак­цию 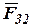. Так как звено 3 находится в равновесии, то геомет­рическая сумма всех сил, действующих на него, равна нулю:

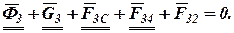
Векторная сумма 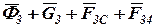 на плане сил (рис. 2) уже имеется. Соединив конец вектора  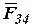с началом вектора  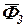получаем искомый вектор 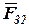. На плане сил он показан пунктиром. Разумеется .

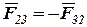На этом заканчивается силовое исследование данной структурной группы