Продолжаем рассматривать неопределенность вида 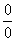
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел 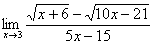
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида 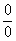 , которую нужно устранять.
, которую нужно устранять.
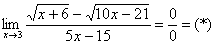
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 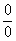 используют метод умножения числителя и знаменателя на сопряженное выражение.
используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов: 
И смотрим на наш предел: 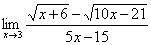
Что можно сказать? 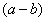 у нас в числителе уже есть. Теперь для применения формулы осталось организовать
у нас в числителе уже есть. Теперь для применения формулы осталось организовать 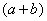 (которое и называется сопряженным выражением).
(которое и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
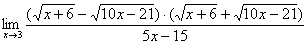
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 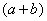 мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на
мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на 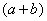 :
:
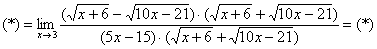
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу  :
:
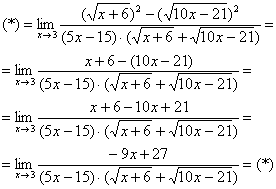
Неопределенность 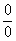 не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
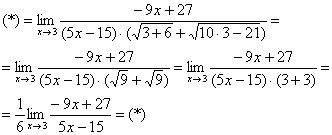
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
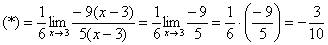
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
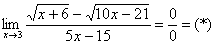
Умножим числитель и знаменатель на сопряженное выражение.
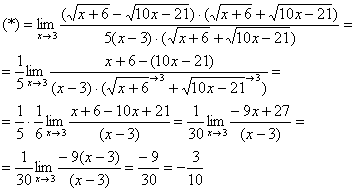
Пример 7
Найти предел 
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
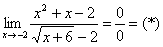
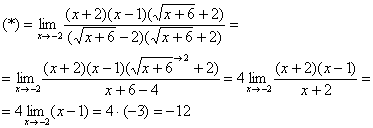 Разложим числитель на множители, а затем умножим числитель и знаменатель на сопряженное выражение
Разложим числитель на множители, а затем умножим числитель и знаменатель на сопряженное выражение
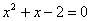
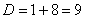
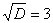
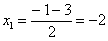
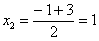
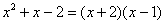
Математический анализ.
Определение. Производной функцииf ( x ) в точке х0 называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю. Обозначается f ’( x ).
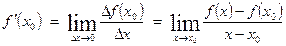
Операция нахождения производной называется дифференцированием функции.
Геометрический смысл производной: производная функции в точке хо равна угловому коэффициенту касательной, проведённой к графику данной функции в данной точке.
Механический смысл производной: мгновенная скорость прямолинейного движения материальной точки в любой момент времени есть производная от пути по времени: 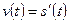
Правила дифференцирования:
1) 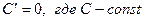 , 2)
, 2) 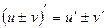 , 3)
, 3)  ,
,
4) 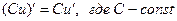 , 5)
, 5) 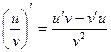 , 6)
, 6) 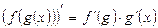 .
.
Таблица производных
| ( xn )′ = n · xn -1 | 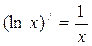
| (sin x)′ = cos x |
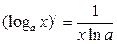
| (cos x)′ = – sin х | (ex)′ = ex |
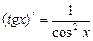
| 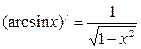
| 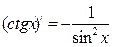
|
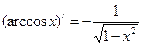
| (ax)′ = ax ·ln a | 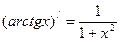
|
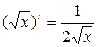
| 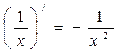
|
Пример1. Найти производную:
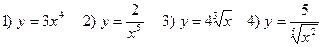
5)  6)
6) 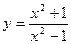
Решение.
1) 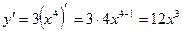 .
.
2) Перепишем функцию в виде, удобном для дифференцирования:  .
.
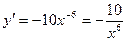 .
.
3) Перепишем функцию в виде, удобном для дифференцирования: 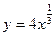 .
.
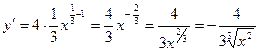 .
.
4) Перепишем функцию в виде, удобном для дифференцирования:  .
.
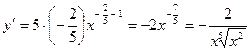 .
.
5) 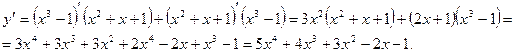
6) 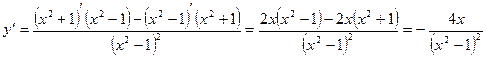 .
.
Пример2. Найти производную сложной функции:
1) 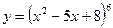 2)
2) 
3) 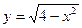 4)
4) 
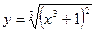 .
.
Решение.
Производная сложной функции вычисляется по правилу дифференцирования 6.
1) 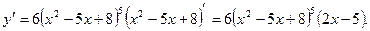
2) Перепишем функцию в виде, удобном для дифференцирования: 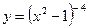 .
.
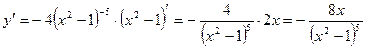
3) 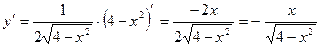 .
.
4) Перепишем функцию в виде, удобном для дифференцирования:  .
.
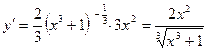 .
.
Определение. Функция F ( x ) называется первообразной для функции f ( x ) на промежутке, если в любой точке этого промежутка её производная равна f ( x ):
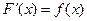 .
.
Отыскание первообразной функции есть действие, обратное дифференцированию, - интегрирование.
Определение. Совокупность первообразных для функции f ( x ) называется неопределённым интегралом и обозначается символом 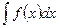 . Таким образом:
. Таким образом:
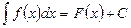 , где f ( x ) dx – подынтегральное выражение, С – постоянная.
, где f ( x ) dx – подынтегральное выражение, С – постоянная.
Свойства неопределённого интеграла.
1) Неопределённый интеграл суммы функций равен алгебраической сумме неопределённых интегралов этих функций.
2) Постоянный множитель подынтегрального выражения можно вынести за знак неопределённого интеграла.
3) Если функция имеет вид f ( kx + b ), то неопределённый интеграл вычисляется по формуле: 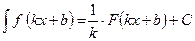 .
.
Таблица первообразных
| B - const | Bx + C |
| x n , n ≠ -1 | 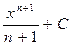
|
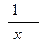
| Ln ( x ) + C |
| e x | e x + C |
| sin x | - cos x + C |
| cos x | sin x + C |
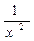
| 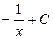
|
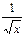
| 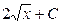
|

| tg x + C |
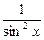
| - ctg x + C |
| ax , a>0 | 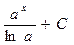
|
Определение. Приращение F ( b ) – F ( a ) любой из первообразных некоторой функции при изменении аргумента от х = а до х = b называется определённым интегралом от а до bфункции f ( x ) и обозначается  . Числа а и b называются пределами интегрирования.
. Числа а и b называются пределами интегрирования.
При вычислении определённого интеграла используется формула Ньютона-Лейбница: 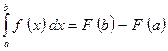 .
.
Пример 3. Найти:
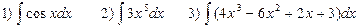 .
.
Решение. 1)  ;
;
2) 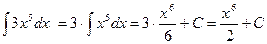 ;
;
3)  .
.
Пример 4. Вычислить:
1) 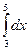 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 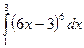 .
.
Решение. 1)  ;
;
2) 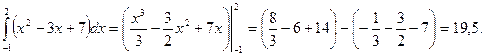
3) 
4) 
Упражнения для тренировки
Найти следующие интегралы:
1. 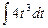
2. 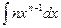
3. 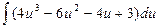
4. 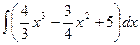
5. 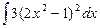
6. 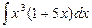
7. 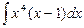
8. 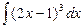
9. 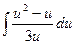
10. 
11. 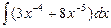
12. 
13. 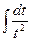
14. 
15. 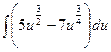
16. 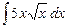
17. 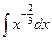
18. 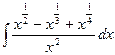
19. 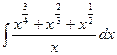
20. 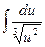
21. 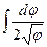
22. 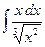
23. 
24. 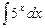
25. 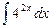
26. 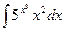
27. 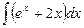
28. 
29. 
30. 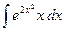
31. 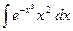
32. 
33. 
34. 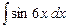
35. 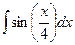
36. 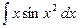
37. 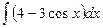
38. 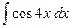
39. 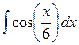
40. 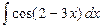
41. 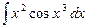
42. 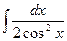
43. 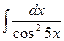
44. 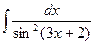
Вычислить определённые интегралы:
45. 
46. 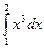
47. 
48. 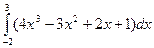
49. 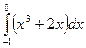
50. 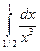
51. 
52. 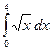
53. 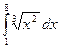
54. 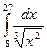
55. 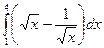
56. 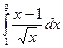
57. 
58. 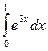
59. 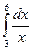
60. 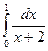
61. 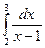
62. 
Дата: 2019-02-02, просмотров: 944.