Рассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой безгранично велики по сравнению с ее толщиной, ось х расположена по нормали к поверхности стенки.
Температура наружной поверхности стенки tст1 и tст2 , причем tст1 > tст2
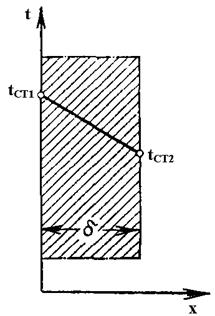Примем, что температура изменяется только в
направлении оси х, т.е. температурное поле
одномерное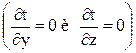 
. Тогда на основании
уравнения теплопроводности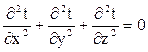 
получим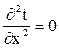 
(1)
Интегрирование этого уравнения приводит к функции
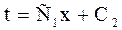(2)
где С1 и С2 – константы интегрирования.
Это уравнение показывает, что по толщине плоской стенки температура изменяется прямолинейно. Константы интегрирования определяются из следующих граничных условий:
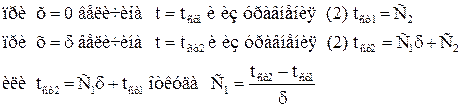
Подставив значение констант в уравнение (2) находим
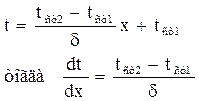
Подставив полученное выражение температурного градиента в уравнение теплопроводности, получим количество переданного тепла:
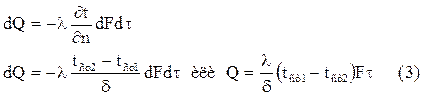
где λ – коэффициент теплопроводности материала стенки, Вт/(м·град);
δ – толщина стенки, м;
tст1 – tст2 – разность температур поверхностей стенки, град;
F – поверхность стенки, м2;
τ – время, сек.
Для непрерывного процесса передачи тепла теплопроводностью т.е.
τ = 0 получим уравнение:
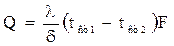(4)
Уравнение (3) и (4) являются уравнениями теплопроводности плоской стенки при установившемся процессе теплообмена.
Если плоская стенка состоит из n – слоев, тогда получим уравнение:
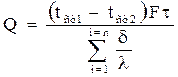
где i – порядковый номер слоя стенки;
n – число слоев.
Теплопроводность цилиндрической стенки
Рассмотрим передачу тепла теплопроводностью через цилиндрическую стенку длиной L внутренним радиусом rВ и наружным радиусом rН.
Температуры на внутренней и внешней стенки постоянны и равны tст1 и tст2
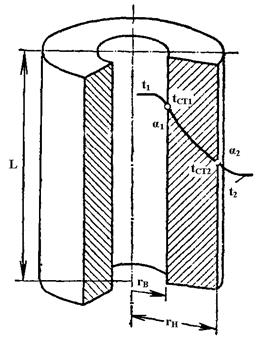
Рассуждая аналогично, получаем уравнение теплопроводности цилиндрической стенки при установившемся процессе теплообмена:
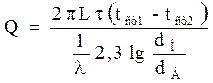
Для многослойной стенки:
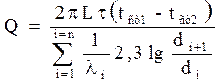
где i – порядковый номер слоя стенки.
Тепловое излучение
Длины волн теплового излучения лежат в основном в невидимой (инфракрасной) части спектра и имеют длину 0,8 – 40мк. Твердые тела обладают сплошным спектром излучения: они способны испускать волны всех длин при любой температуре. Однако интенсивность теплового излучения с увеличением температуры возрастает и при высоких температурах t ≥ 6000 С лучистый теплообмен становится доминирующим.
Пусть Q – общая энергия падающих на тело лучей; Qпогл. – энергия, поглощаемая телом; Qотр. – энергия, отраженная от поверхности тела, и
Qпр – энергия лучей проходящих сквозь тело без изменения.
Тогда баланс тепла составит:
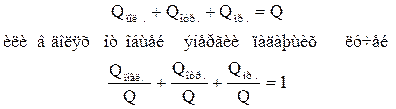
Если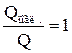 
, а 
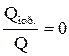и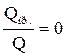 
, то тело поглощает все падающие на него лучи и является абсолютно черным.
Если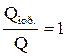 
, то тело отражает все лучи и называется абсолютно белым.
Если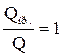 
, то тело пропускает все падающие лучи и называется абсолютно прозрачным или диатермичным.
Закон Стефана – Больцмана: лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры его поверхности.
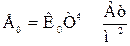
где Т – абсолютная температура поверхности тела, 0К;
К0 = 5,67·10-8 , Вт/(м2·0К4) – константы лучеиспускания абсолютно черного тела.
Закон Кирхгофа: для серых тел необходимо знать зависимость между их излучательной и поглощательной способностью.
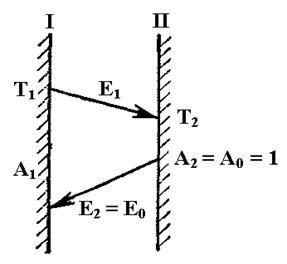
I – серое тело;
II – абсолютно черное тело.
Температура серого тела
выше, чем абсолютно черного Т1 > Т2
Поглощательная способность
серого тела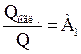 
Для абсолютно черного тела
А2 = А0 = 1
Тогда количество тепла (на единицу поверхности в единицу времени), переданного серым телом путем излучения, составляет:
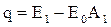
При достижении теплового равновесия Т1 = Т2, при котором q = 0 и следовательно:
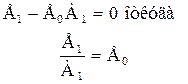
Тогда для ряда взаимно параллельных тел получим:
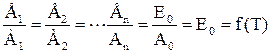
т.е. отношение лучеиспускательной способности черного тела к его лучепоглащательной способности при той же температуре является величиной постоянной, равной лучеиспускательной способности абсолютно черного тела.
Дата: 2019-02-02, просмотров: 256.
