При увеличении силы Р стержень вначале будет оставаться прямым , и если ему даже дать искусственное небольшое отклонение У, то после устранения причины отклонения он вернется к первоначальному прямолинейному положению (устойчивое равновесие). При дальнейшем увеличении внешней нагрузки Р может наступить такой момент, когда будут возможны прямолинейная форма равновесия стержня и криволинейная, изгибная. В этом случае при небольшом искусственном отклонении стержня на величину У и устранения причины отклонения стержень останется изогнутым и не вернется к прямолинейному положению. В точке разветвления прямолинейной криволинейной форм равновесия внешняя сила достигнет своего критического значения N_сч. Дальнейшее, самое незначительное увеличение силы N_сч ведет к резкому нарастанию деформаций и потере несущей способности стержня. Критическая сила для упругого, центрально сжатого, шарнирно – опертого по концам стержня определяется по формуле Л. Эйлера (1744 г.):

_,

где Е – модуль упругости материала стержня;

J – минимальный момент инерции сечения стержня;

 – расчетная длина стержня.

Критические напряжения в стержне:

,

где – площадь брутто поперечного сечения стержня;

 – радиус инерции стержня;

 –- гибкость стержня.

Критические напряжения зависят только от гибкости стержня l. При выводе формулы Эйлера предполагалось что модуль упругости материала Е имеет постоянное значение. Поэтому для строительных сталей формула справедлива только в пределах пропорциональности. Минимальная гибкость для стального стержня, выше которой формула Эйлера будет справедлива:

.

Абсолютно прямолинейный стержень является идеализированной расчетной схемой. Все реальные стержни в натуре имеют неизбежные отклонения от прямолинейности (случайные эксцентриситеты ). Поэтому с самого начала загружения центрально сжатого стержня в нем возникает изгибающий момент , что ухудшает условия устойчивости стержня и снижает его критические напряжения. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней. Устойчивость центрально сжатого стержня будет обеспечена, если напряжение в нем будут меньше критических:

.

Чтобы не определять для каждого стержня критические напряжения, а иметь дело с расчетным сопротивлением стали R_y, критические напряжения выражают через расчетное сопротивление стали, умноженное на коэффициент продольного изгиба (меньший единицы):

.

тогда .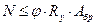

Или, переписав это выражение в принятой форме сравнения напряжений в стержне с расчетным сопротивлением стали, получим расчетную формулу проверки устойчивости стержня при центральном сжатии, принятую в нормах:

.

Коэффициент продольного изгиба  принимается по таблицам СНиП в зависимости от класса стали и гибкости элемента , определяемой по формуле:

,

где  – коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня;

 – радиус инерции сечения стержня;

 - расчетная длина стержня;

 – геометрическая длина стержня.

Значения коэффициентов  для сталей разных классов и некоторых алюминиевых сплавов приведены в нормах проектирования.