концепция рандомизации;

концепция последовательного эксперимента;

концепция математического моделирования;

концепция оптимального использования факторного пространства и ряд других.

Принцип рандомизации заключается в том, что в план эксперимента вводят элемент случайности. Для этого план эксперимента составляется таким образом, чтобы те систематические факторы, которые трудно поддаются контролю, учитывались статистически и затем исключались в исследованиях как систематические ошибки.

При последовательном проведении эксперимент выполняется не одновременно, а поэтапно, с тем, чтобы результаты каждого этапа анализировать и принимать решение о целесообразности проведения дальнейших исследований (рис.2.1). В результате эксперимента получают уравнение регрессии, которое часто называют моделью процесса.

Для конкретных случаев математическая модель создается исходя из целевой направленности процесса и задач исследования, с учетом требуемой точности решения и достоверности исходных данных.

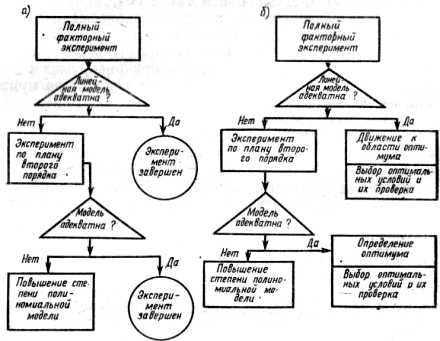
Рис 10.9. Структурная схема эксперимента:

а) - с целью математического описания исследуемого процесса;

б) - с целью оптимизации исследуемого процесса

В настоящее время изданы каталоги планов эксперимента , в которых приводятся сравнительная оценка планов и рекомендации по их выбору применительно к конкретным условиям эксперимента.

Важное место в теории планирования эксперимента занимают вопросы оптимизации исследуемых процессов, свойств многокомпонентных систем или других объектов.

Как правило, нельзя найти такое сочетание значений влияющих факторов, при котором одновременно достигается экстремум всех функций отклика. Поэтому в большинстве случаев за критерий оптимальности выбирают лишь одну из переменных состояния функцию отклика, характеризующую процесс, а остальные принимают приемлемыми для данного случая.

Методы планирования эксперимента в настоящее время быстро развиваются, чему способствует возможность широкого использования ЭВМ.

Вычислительным экспериментом называется методология и технология исследований, основанные на применении прикладной математики и электронно-вычислительных машин как технической базы при использовании математических моделей.

Таким образом, вычислительный эксперимент основывается на создании математических моделей изучаемых объектов, которые формируются с помощью некоторой особой математической структуры, способной отражать свойства объекта, проявляемые им в различных экспериментальных условиях.

Однако эти математические структуры превращаются в модели лишь тогда, когда элементам структуры дается физическая интерпретация, когда устанавливается соотношение между параметрами математической структуры и экспериментально определенными свойствами объекта, когда характеристики элементов модели и самой модели в целом находят соответствие свойствам объекта.

Таким образом, математические структуры вместе с описанием соответствия экспериментально обнаруженным свойствам объекта и являются моделью изучаемого объекта, отражая в математической, символической (знаковой) форме объективно существующие в природе зависимости, связи и законы.

Каждый вычислительный эксперимент основывается как на математической модели, так и на приемах вычислительной математики. Современная вычислительная математика состоит из многих разделов развивающихся вместе с развитием электронно-вычислительной техники.

На основе математического моделирования и методов вычислительной математики создались теория и практика вычислительного эксперимента, технологический цикл которого принято разделять на следующие этапы.

1. Для исследуемого объекта строится модель, обычно сначала физическая, фиксирующая разделение всех действующих и рассматриваемом явлении факторов на главные и второстепенные, которые на данном этапе исследования отбрасываются.

Одновременно формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты. Модель записывается в математических терминах, как правило, в виде дифференциальных или интегродиф-ференциальных уравнений.

2. Разрабатывается метод расчета сформулированной математической задачи. Эта задача представляется в виде совокупности алгебраических формул, по которым должны вестись вычисления и условия, показывающие последовательность применения этих формул; набор этих формул и условий носит название вычислительного алгоритма.

Вычислительный эксперимент имеет многовариантный характер, так как решения поставленных задач часто зависят от многочисленных входных параметров. Тем не менее каждый конкретный расчет в вычислительном эксперименте проводится при фиксированных значениях всех параметров.

Между тем в результате такого эксперимента часто ставится задача определения оптимального набора параметров. Поэтому при создании оптимальной установки приходится проводить большое число расчетов однотипных вариантов задачи, отличающихся значением некоторых параметров. В связи с этим при организации вычислительного эксперимента можно использовать эффективные численные методы.

3. Разрабатываются алгоритм и программа решения задачи на ЭВМ. Программирование решений определяется теперь не только искусством и опытом исполнителя, а перерастает в самостоятельную науку со своими принципиальными подходами.

4. Проведение расчетов на ЭВМ. Результат получается в виде некоторой цифровой информации, которую далее необходимо будет расшифровать. Точность информации определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания).

5. Обработка результатов расчетов, их анализ и выводы. На этом этапе могут возникнуть необходимость уточнения математической модели (усложнения или, наоборот, упрощения), предложения по созданию упрощенных инженерных способов решения и формул, дающих возможности получить необходимую информацию более простым способом.

Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными.

В науке и технике известно немало областей, в которых вычислительный эксперимент оказывается единственно возможным при исследовании сложных систем.