При соотношении параметров контура из конденсатора, катушки и резистора 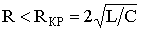 , где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:
, где RКР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:
p1,2 = -α ± jω,
где α = R / (2L) – коэффициент затухания свободной составляющей;
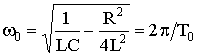 – угловая частота собственных колебаний контура;
– угловая частота собственных колебаний контура;
Т0 – период собственных колебаний.
Поскольку 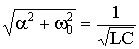 , то можно ввести обозначения
, то можно ввести обозначения
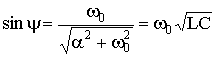 ,
, 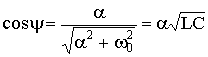 ,
, 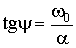 .
.
Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1)
uCсв = A e-αt sin(ω0t + ψ),
Для свободной составляющей тока 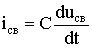 имеем
имеем
iсв = C A e-αt (-α sin(ω0t + ψ) + ω0 cos(ω0t + ψ)).
С учетом начальных условий при t = 0, uC = U0 , i = 0 из последних двух уравнений находим константы интегрирования:
U0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cos ψ).
и далее
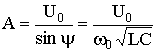 .
.
Запишем переходные напряжения и ток:
uC = UCm e-αt sin(ω0t + ψ);
i = -Im e-αt sin(ω0t + π);
uL= ULm e-αt sin(ω0t - ψ),
где 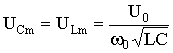 ;
; 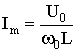 .
.
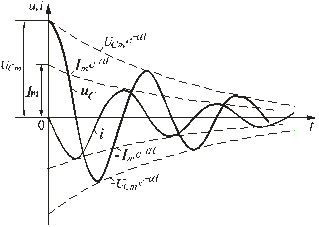
Рис. 5.15
Зависимости переходных напряжения и тока uC, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т0, например:
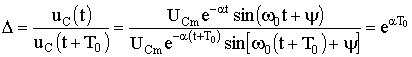 .
.
Часто пользуются логарифмическим декрементом колебания:
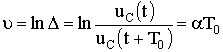 .
.
В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона 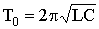 , а частота незатухающих колебаний
, а частота незатухающих колебаний 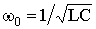 .
.
Включение контура из конденсатора, резистора, катушки на постоянное напряжение
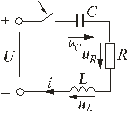
Рис. 5.16
Рассмотрим электромагнитные процессы, возникающие после замыкания ключа в цепи, изображенной на рис. 5.16 в предположении, что конденсатор был предварительно не заряжен, т.е. uC(0-) = 0. Характеристическое уравнение и вид его корней будут такими же, как и в цепи, рассмотренной в п. 5.6.
Апериодический процесс
Между разрядом конденсатора на резистор с катушкой и включением на постоянное напряжение контура (см. рис. 5.16) существует аналогия. Так же, как при разряде конденсатора, установившаяся составляющая тока равна нулю. Установившееся напряжение на конденсаторе uCу = U. Следовательно, начальное значение свободной составляющей напряжения на конденсаторе
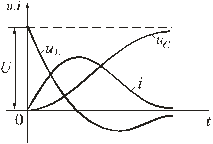
Рис. 5.17
uCсв(0+) = uC(0+) - uCу(0-)
равно uCсв(0+) = -U. То есть знаки постоянных интегрирования А1 и А2 в отличие от рассмотренного в п. 5.6 случая изменяются на противоположные. В этом случае переходное напряжение на конденсаторе, ток и напряжение на катушке определяются по формулам:
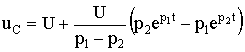 ;
;
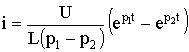 ;
; 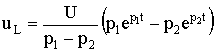 .
.
Кривые uC(t), uL(t) и i(t) приведены на рис. 5.17.
Колебательный процесс
Включение рассматриваемого контура на постоянное напряжение может сопровождаться колебательным переходным процессом. При этом в отличие от процесса разряда конденсатора (см. п. 5.6) знак начального значения преходящего напряжения, следовательно, и коэффициента А, изменится на противоположный. Переходные напряжения и ток приобретут вид:
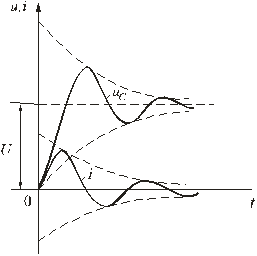
Рис. 5.18
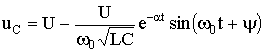 ;
;
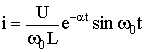 ;
;
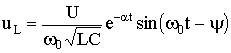 .
.
Кривые uC(t) и i(t) показаны на рис. 5.18. Кривая тока отображает затухающие колебания относительно нулевого значения, а напряжения на конденсаторе – относительно установившегося значения. Следует отметить, что за время переходного процесса контура часть энергии источника переходит в тепло, а другая часть запасается в электрическом поле конденсатора в виде:
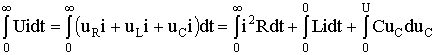
т.е. 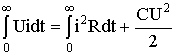 .
.
Дата: 2019-02-02, просмотров: 305.