Кафедра: «Механика»
Расчетно-проектировочная работа
по дисциплине «Прикладная механика»
05 вариант
| ВЫПОЛНИЛ | |
| (студент, курс, группа) | |
| ПРОВЕРИЛ | |
| (фамилия, имя, отчество) | |
| Допуск к защите | |
| (дата) | |
| (оценка и роспись руководителя) |
г.Самара
2014г
Содержание
Задача №1 Расчет стержня при центральном растяжении или сжатии. 3
Задача №2 Расчет балки на прочность по нормальным напряжениям. 6
Задача №3 Расчет круглого прямого бруса (вала) на прочность и жесткость при кручении. 10
Задача №1 Расчет стержня при центральном растяжении или сжатии.
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P1 | 5 | кН |
| P2 | 15 | кН |
| a | 0,2 | м |
| b | 0,1 | м |
| [s] | 80 | МПа |
| Форма сечения | круг | |
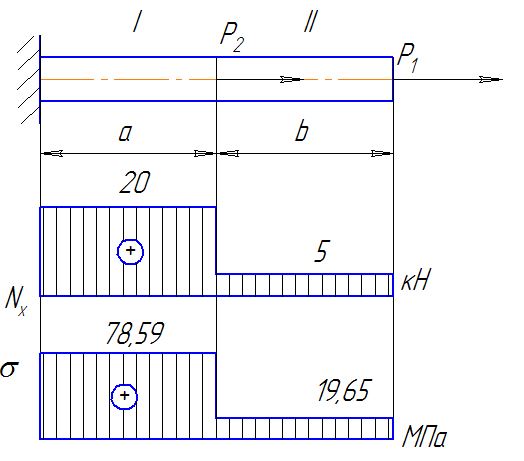
Стержень закреплен жёстко одним концом и к нему приложены две внешние силы Р1 и Р2, направление которых и точки их приложения совпадают с продольной осью стержня.
Стержень состоит из двух участков. Обозначим их, начиная с закрепленного конца, цифрами I и II.
1. Проведём на участке I произвольное сечение и рассмотрим равновесие правой отсеченной части:
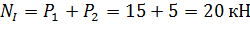
Знак перед числом говорит о том, что участок испытывает деформацию сжатия.
Проведем произвольное сечение на участке II. Определим нормальную (продольную) силу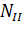 
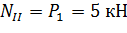
Данный участок испытывает деформацию растяжения.
Строим эпюру изменения продольной силы N(x) по длине стержня под расчетной схемой с соблюдением масштаба.
2. Определим размеры поперечного сечения из условия прочности при растяжении (сжатии):
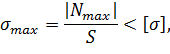
откуда следует:
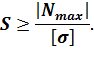
Из эпюры продольной силы видно, что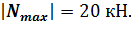 
Следовательно,
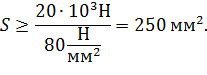
Принимая из условия задачи, что сечение - круг, определяем его радиус: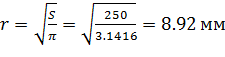 
Округляем в сторону увеличения до целого числа, т.е. принимаем r=9 мм. Тогда площадь поперечного сечения стержня будет равна
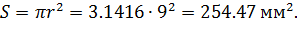
Определим напряжения в поперечных сечениях стержня на обоих участках:
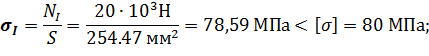
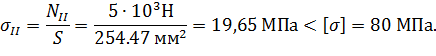
Условие выполняется.
Строим эпюру изменения напряжения растяжения (сжатия) по длине стержня под эпюрой продольной силы с соблюдением масштаба.
4. Определим абсолютную упругую деформацию стержня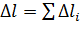 
, в нашем случае: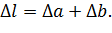 
Деформация на 1 участке:
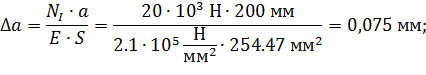
Деформация на 2 участке:
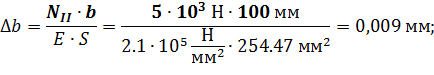
Таким образом, суммарная абсолютная упругая деформация равна:
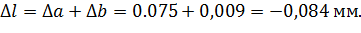
Ответ:
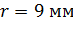
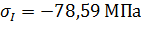
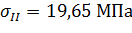
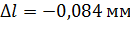
Задача №2 Расчет балки на прочность по нормальным напряжениям
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P | 3 | кН |
| M | 6 | кН*м |
| q | 5 | кН/м |
| a | 2 | м |
| b | 4 | м |
| [s] | 120 | МПа |
| Форма сечения | Прямоугольник b/h=0.4 | |
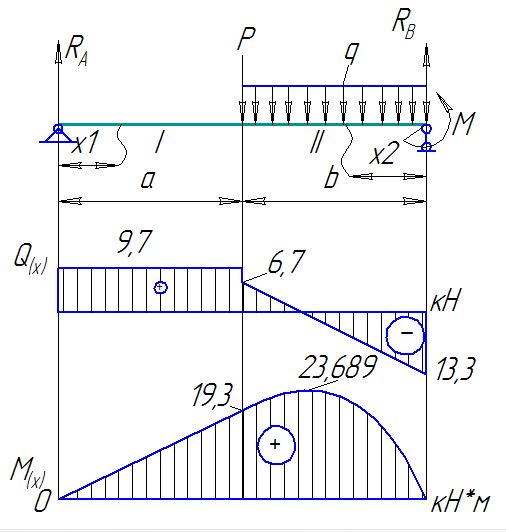
1. Обозначим реакции опор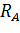 
и 
и 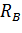определим их величину, используя уравнения равновесия для плоской системы сил:
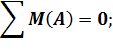
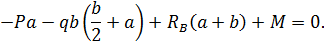
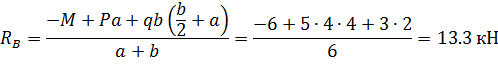
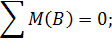
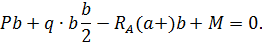
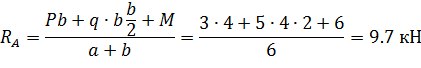
Проверка:
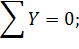
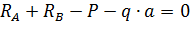
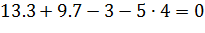
Реакции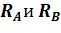 
определены верно.
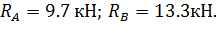
Нахождение точки экстремума
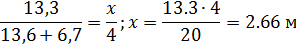
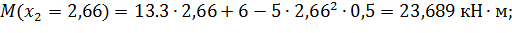
Строим эпюру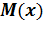 
3. Определяем размеры поперечного сечения, используя условие прочности:
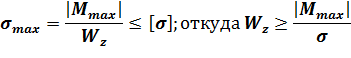
Из эпюры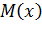 
видно, что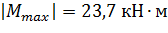 
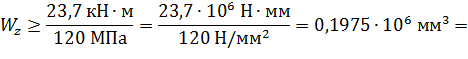
Кафедра: «Механика»
Расчетно-проектировочная работа
по дисциплине «Прикладная механика»
05 вариант
| ВЫПОЛНИЛ | |
| (студент, курс, группа) | |
| ПРОВЕРИЛ | |
| (фамилия, имя, отчество) | |
| Допуск к защите | |
| (дата) | |
| (оценка и роспись руководителя) |
г.Самара
2014г
Содержание
Задача №1 Расчет стержня при центральном растяжении или сжатии. 3
Задача №2 Расчет балки на прочность по нормальным напряжениям. 6
Задача №3 Расчет круглого прямого бруса (вала) на прочность и жесткость при кручении. 10
Задача №1 Расчет стержня при центральном растяжении или сжатии.
Исходные данные:
| Наименование параметра | Значение | Единица измерения |
| P1 | 5 | кН |
| P2 | 15 | кН |
| a | 0,2 | м |
| b | 0,1 | м |
| [s] | 80 | МПа |
| Форма сечения | круг | |
Стержень закреплен жёстко одним концом и к нему приложены две внешние силы Р1 и Р2, направление которых и точки их приложения совпадают с продольной осью стержня.
Стержень состоит из двух участков. Обозначим их, начиная с закрепленного конца, цифрами I и II.
1. Проведём на участке I произвольное сечение и рассмотрим равновесие правой отсеченной части:
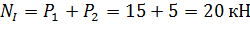
Знак перед числом говорит о том, что участок испытывает деформацию сжатия.
Проведем произвольное сечение на участке II. Определим нормальную (продольную) силу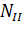
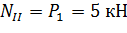
Данный участок испытывает деформацию растяжения.
Строим эпюру изменения продольной силы N(x) по длине стержня под расчетной схемой с соблюдением масштаба.
2. Определим размеры поперечного сечения из условия прочности при растяжении (сжатии):
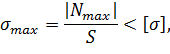
откуда следует:
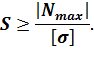
Из эпюры продольной силы видно, что 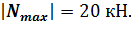Следовательно,
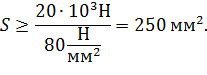
Принимая из условия задачи, что сечение - круг, определяем его радиус: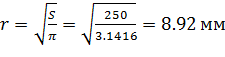
Округляем в сторону увеличения до целого числа, т.е. принимаем r=9 мм. Тогда площадь поперечного сечения стержня будет равна
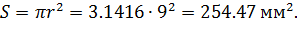
Дата: 2019-02-02, просмотров: 214.
