Создаем новый проект, выбираем тип схемы: 2 ­ Плоская рама.

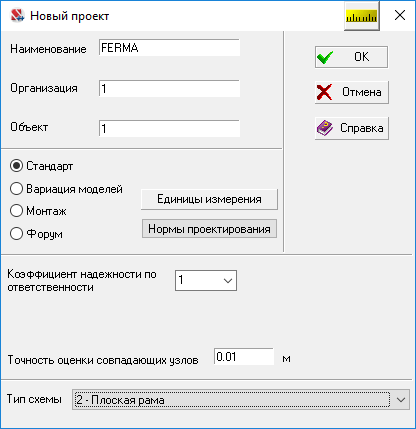
Рисунок 1.14 ­ Создаем новый проект

Выбираем:

Расчетная схема ­ Графический препроцессор    ­ Геометрия.

На вкладке «Узлы и элементы», нажимаем ввод узлов и по координатам вводим все узлы фермы.

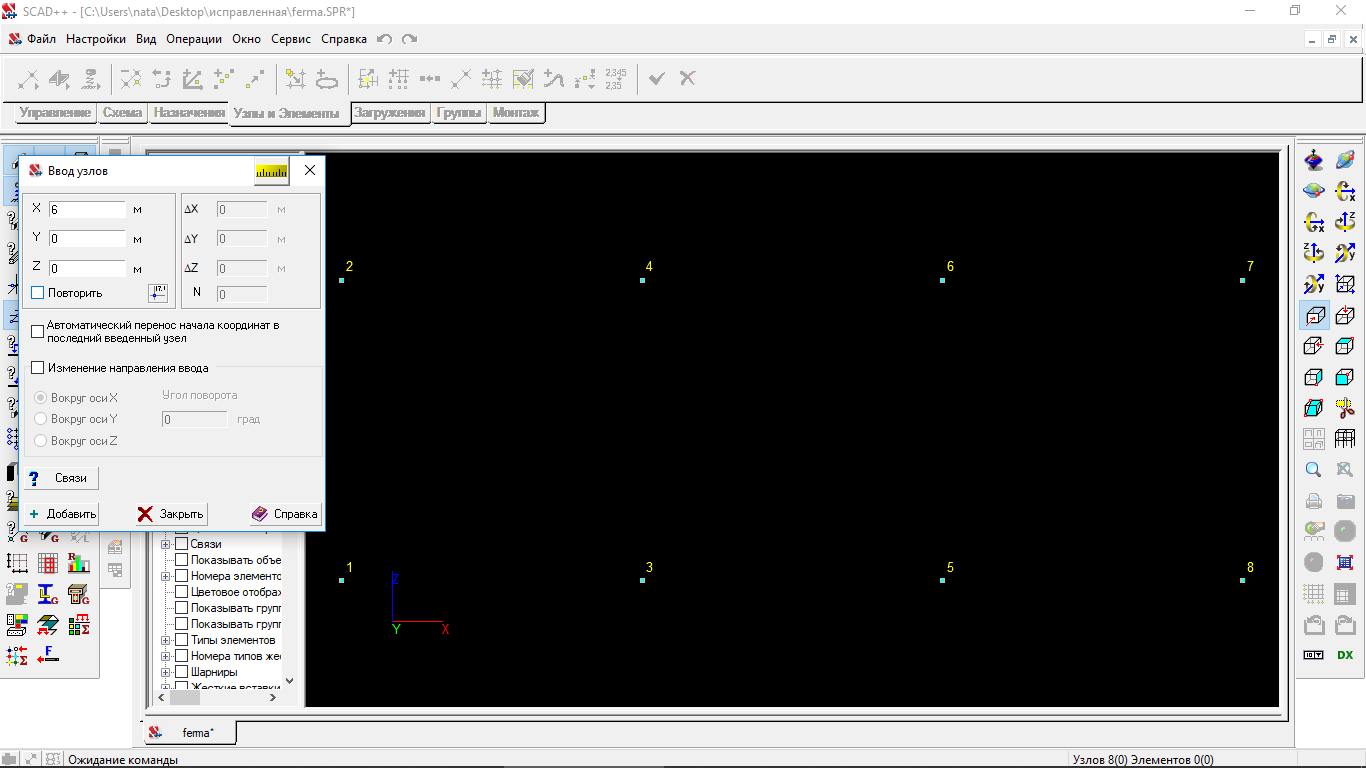
Рисунок 1.15 ­ Вводим узлы фермы по координатам

При вводе стержней сразу задаем и жесткость элементов, например, профили металлопроката, квадратная труба 100х5.

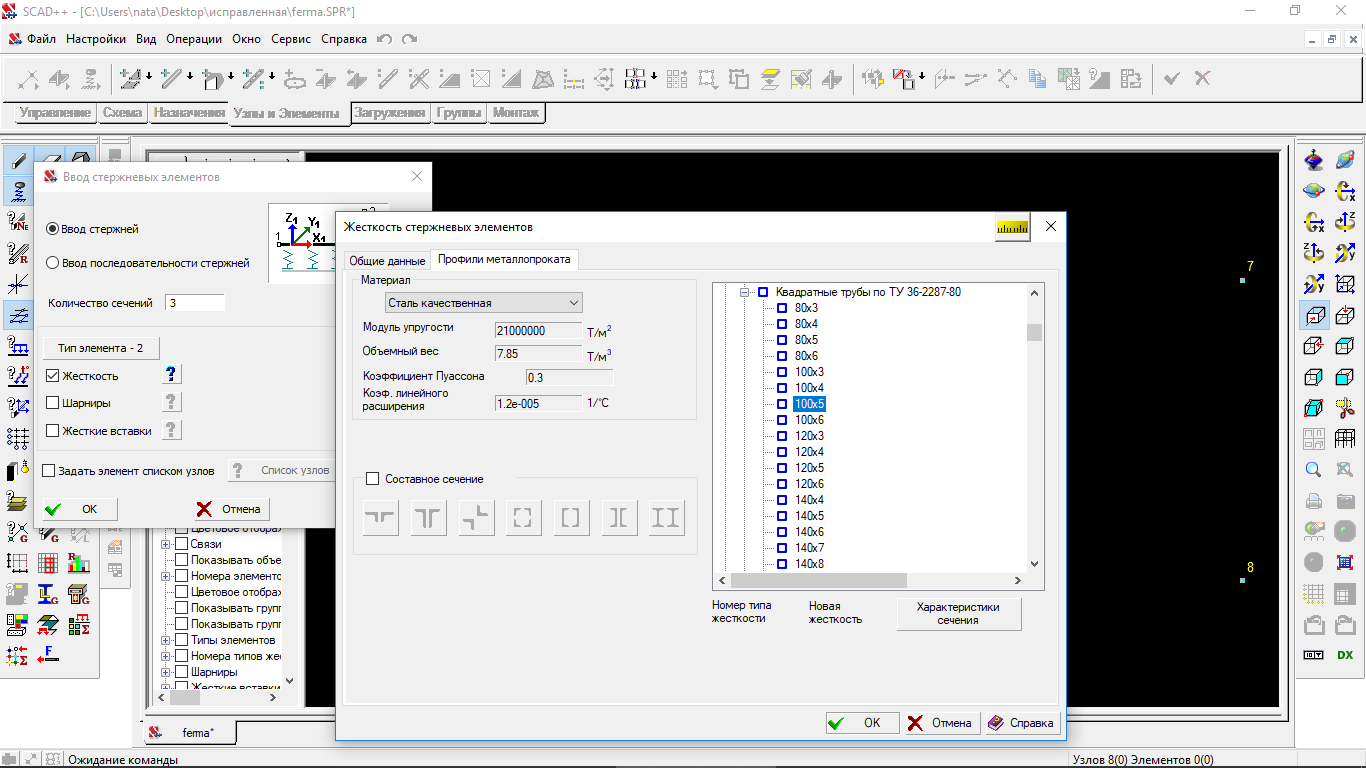
Рисунок 1.16 ­ Ввод стержней, задание жесткости стержневых элементов

Задаем элемент списком узлов, прописываем начальный и конечный узел.

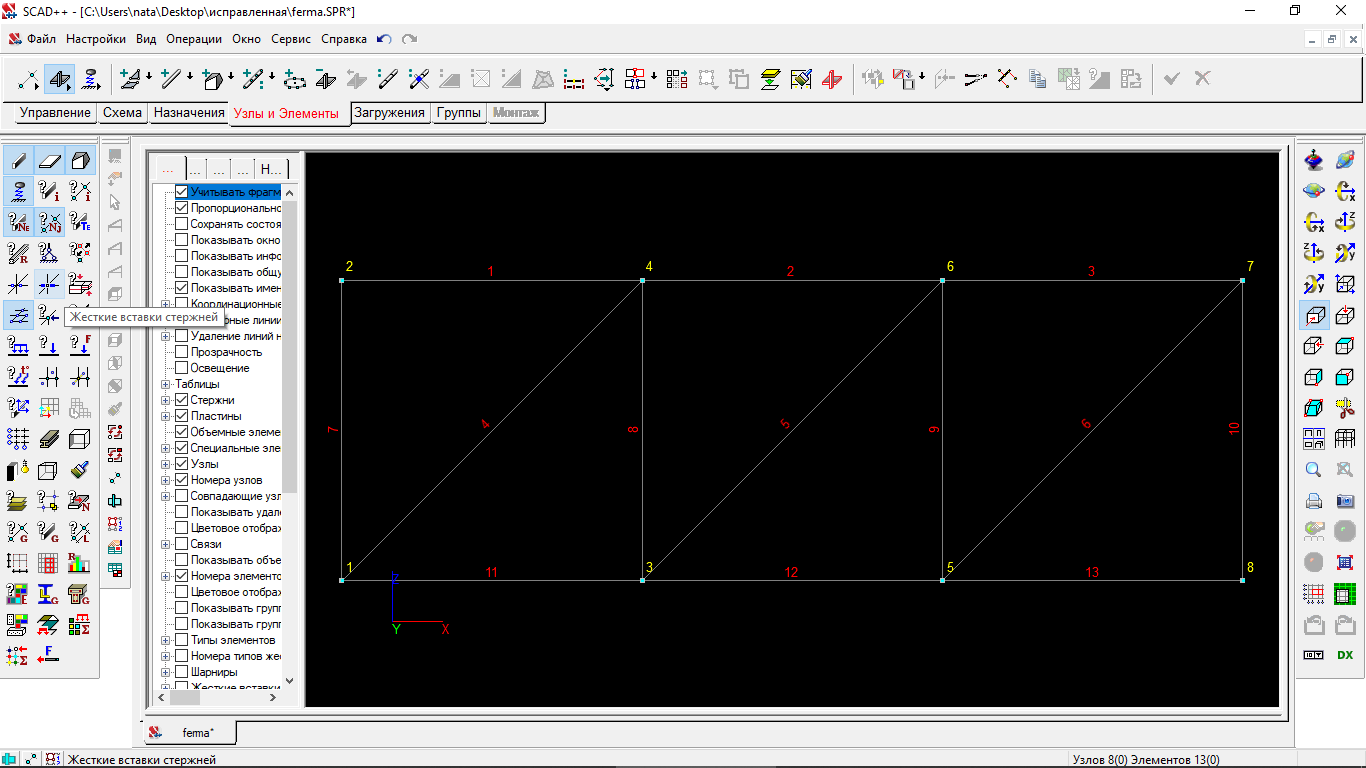
Рисунок 1.17 ­ Ввод стержней

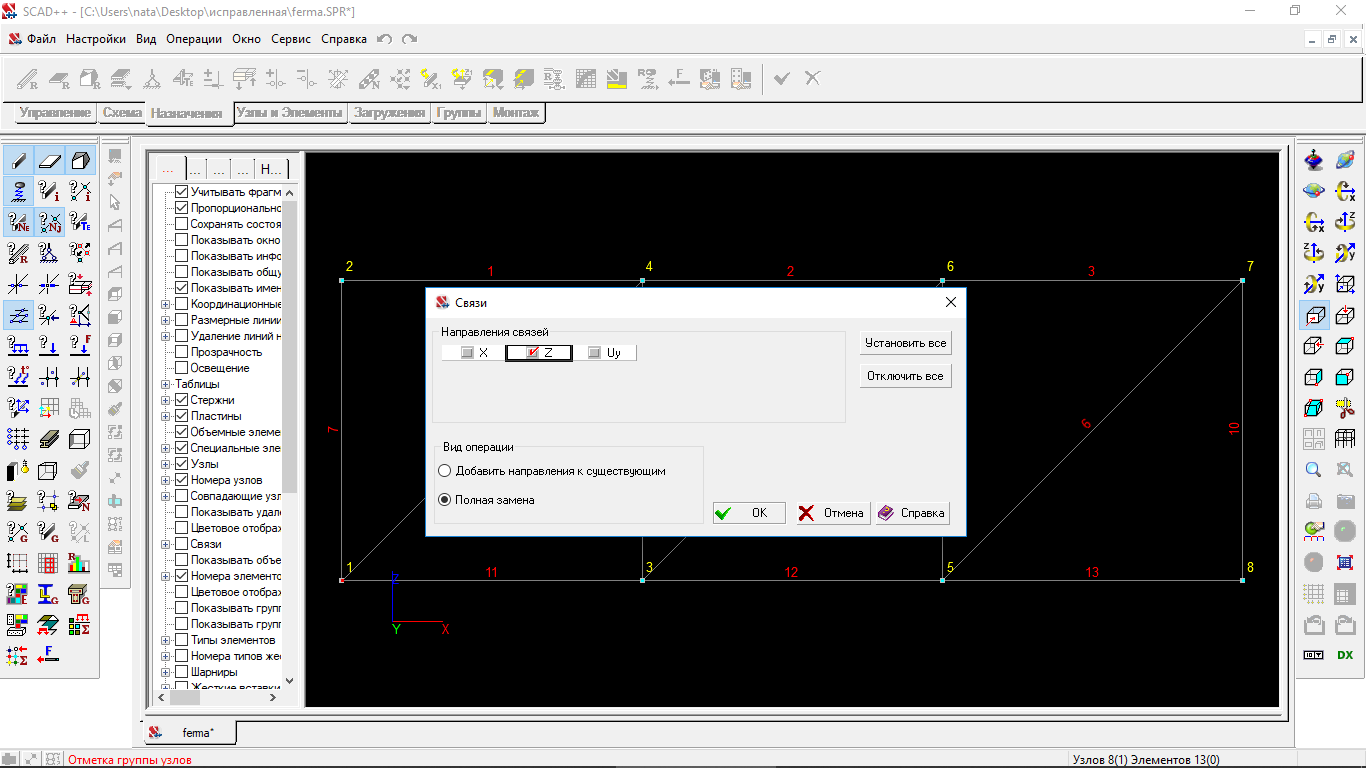
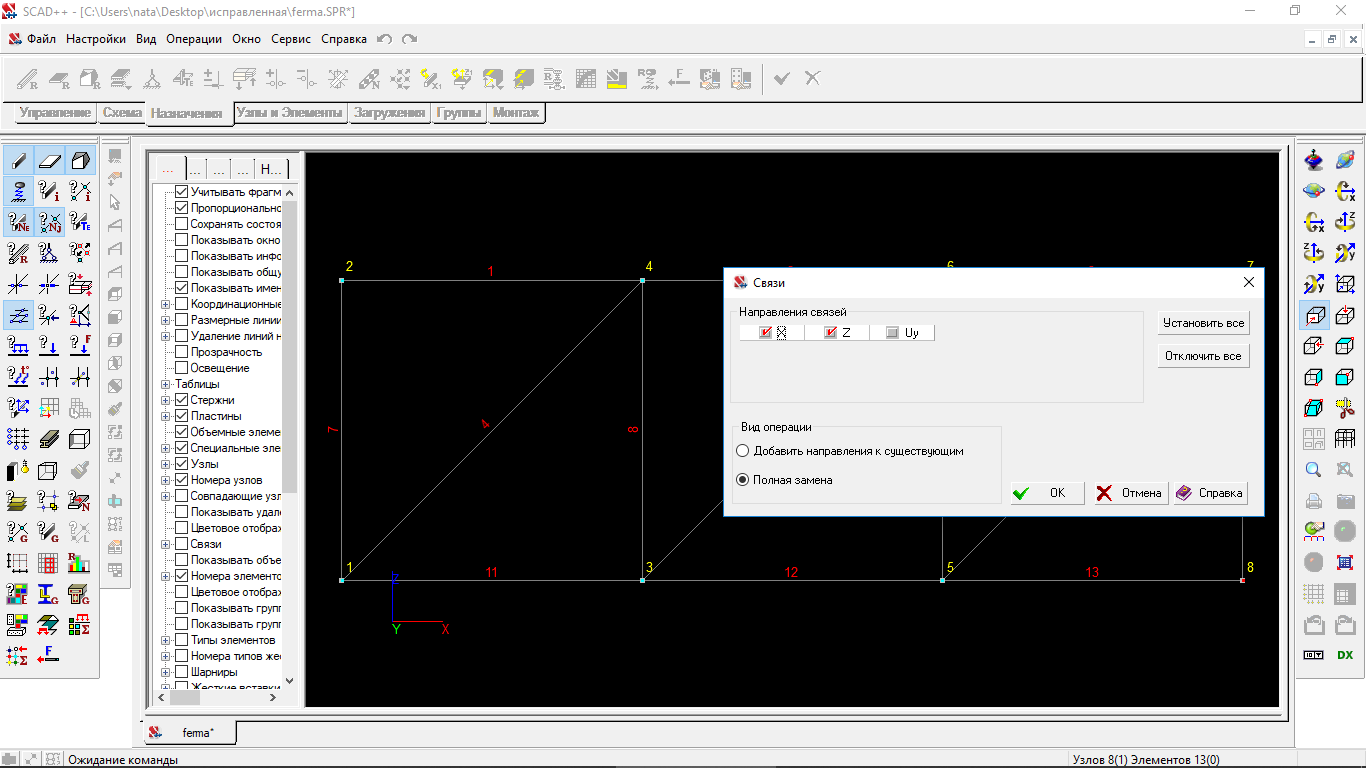
Назначаем связи для крайних узлов:

Рисунок 1.18 ­ Назначение связей

На вкладке «Назначения» выбираем «Установка шарниров» и задаем примыкание стержней друг к другу, предварительно выделив все элементы фермы.

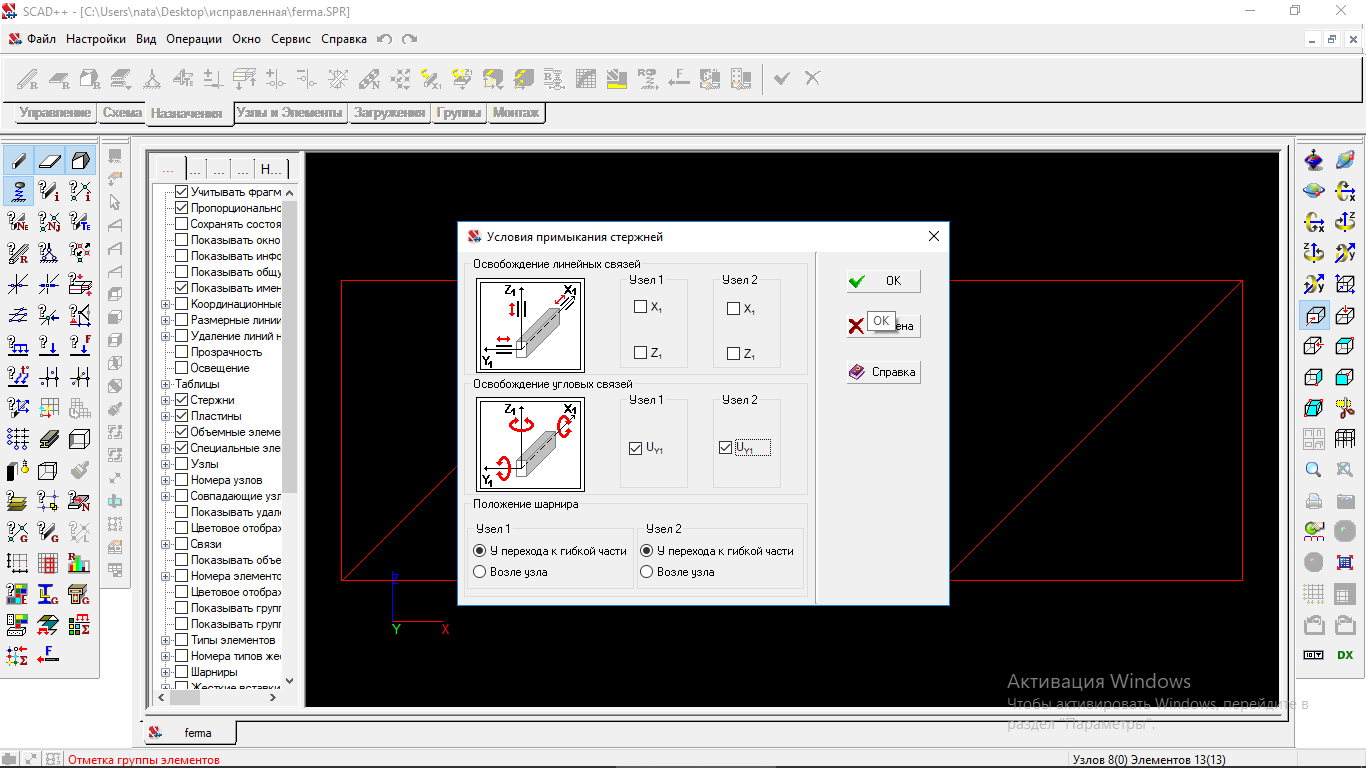
Рисунок 1.19 ­ Установка примыкания стержней

На вкладке «Загружение» выбираем «Узловые нагрузки», предварительно выделив узлы верхнего пояса фермы. По оси Z задаем единичную нагрузку.

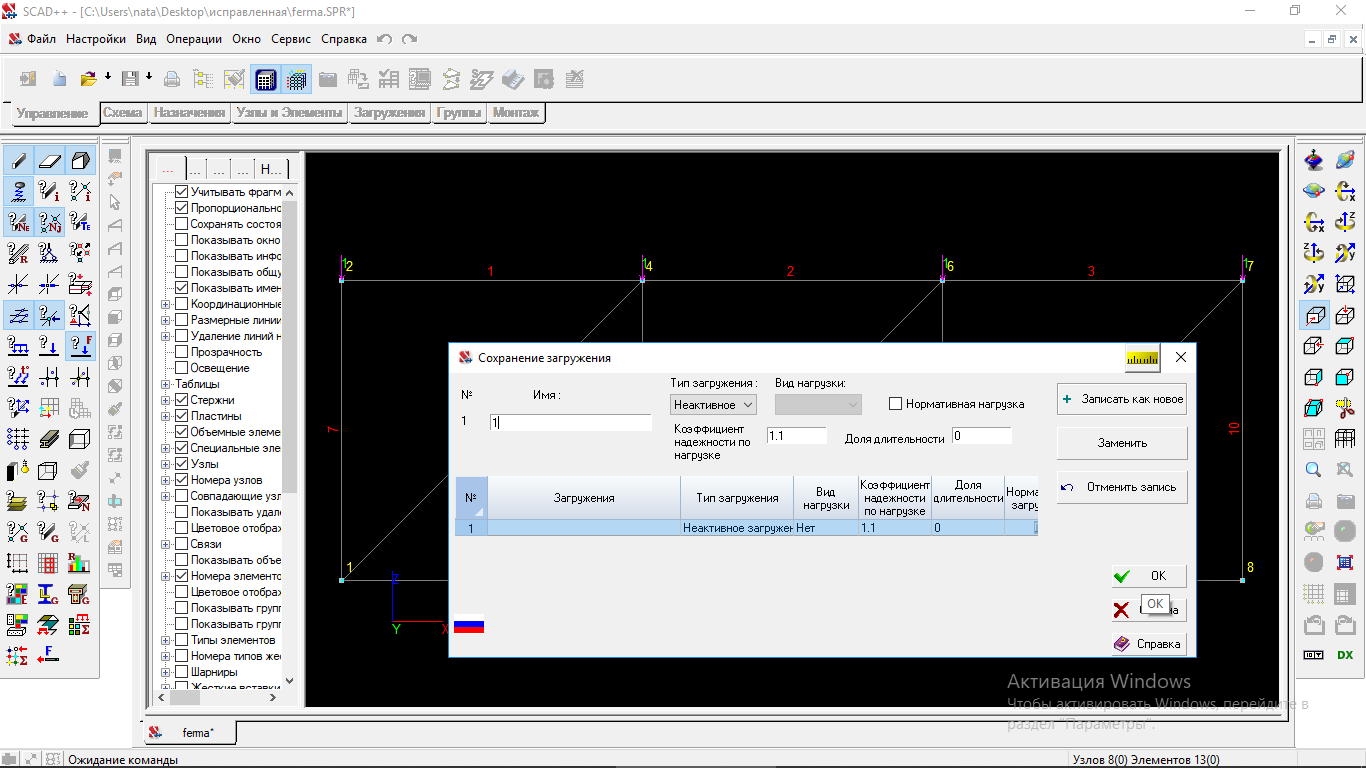
Рисунок 1.20 ­ Сохраняем загружение

Выполняем линейный расчет.

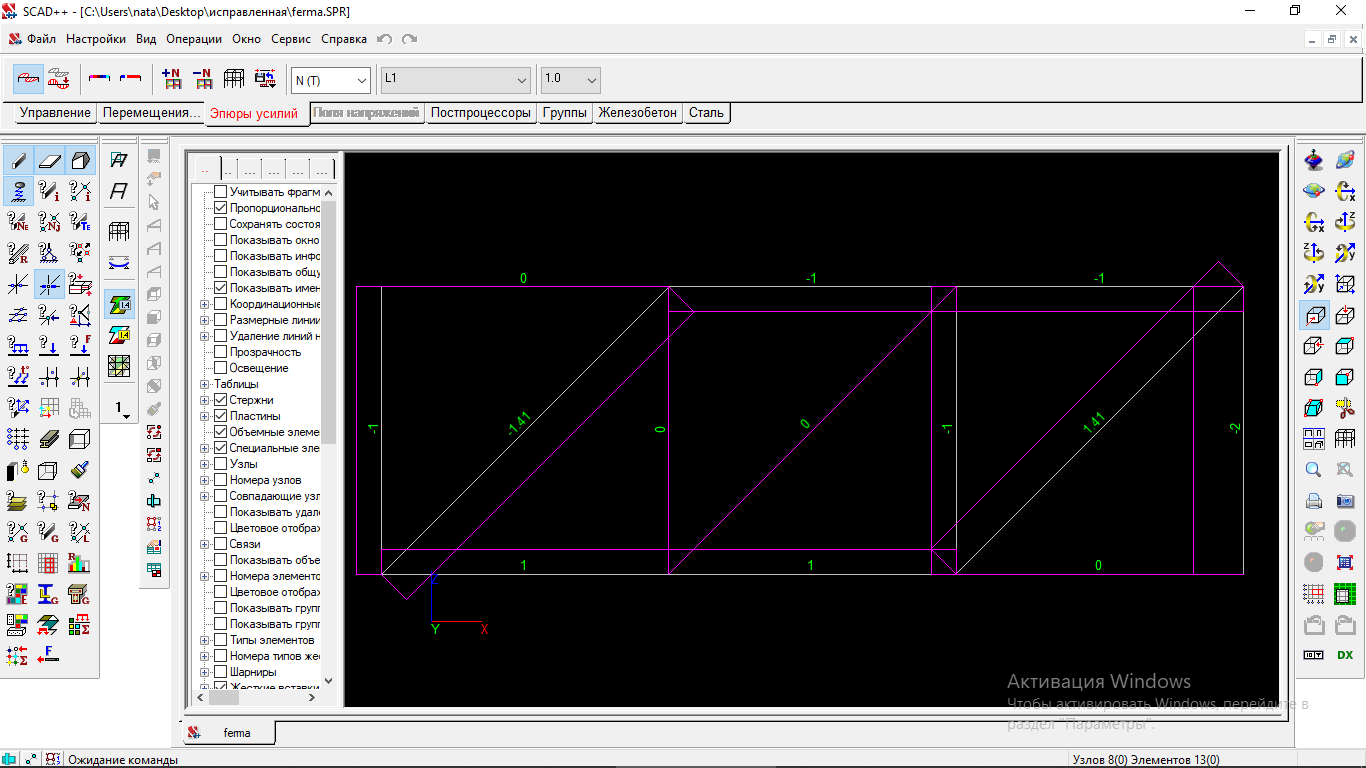
Рисунок 1.21 ­ Результаты линейного расчета: Эпюра «N»

Результаты расчета усилий в стержнях статически определимой фермы также полностью совпадают 100% с предыдущими результатами, выполненными в MathCAD и LiraSAPR2013.

Применение общей системы равновесия строительной механики
к расчету статически определимых многопролетных балок

Рассмотрим расчет многопролетной балки, показанной на рисунке 3.1

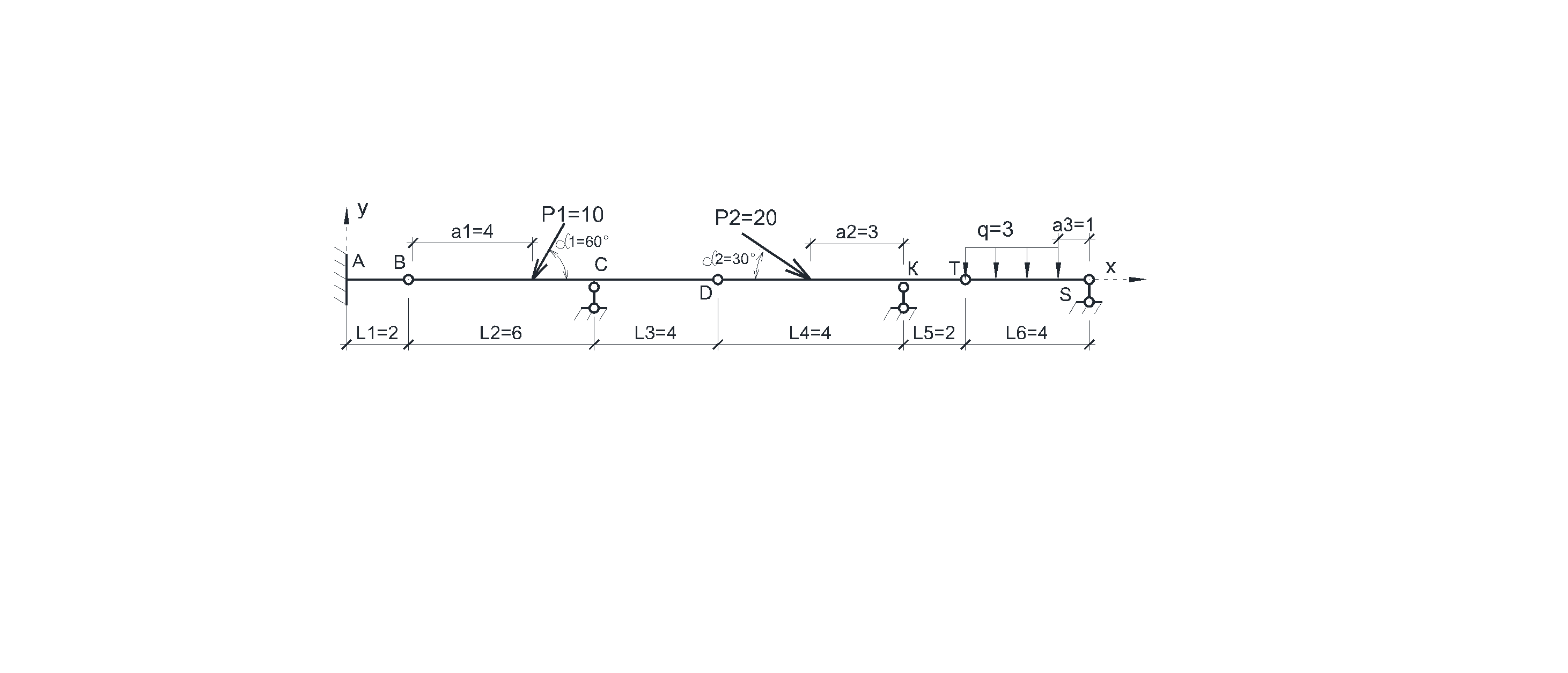 Рисунок 2.1 ­ Статически определимая многопролетная балка

Каждая из простых балок – это диск, который имеет три степени свободы, равновесие которого описывается тремя уравнениями равновесия. Каждый шарнир, соединяющий балки, имеет две связи и при его разрезании в нем возникает соответственно две внутренние реактивные силы. Рассматриваемая многопролетная балка состоит из четырех простых балок, и для них соответственно можно составить двенадцать уравнений равновесия. Разделив многопролетную балку по трем шарнирам B, D, T на простые балки, получим в качестве неизвестных шесть внутренних реактивных сил и шесть опорных реакций в опорах.

Разобьём балку на простые балки. Обозначим реакции опор RА, HA, MRA, RС, RК ,RS и неизвестные в шарнирах XB, YB , XD, YD , XT, YT .

Используя общий подход, следует составить уравнения равновесия для каждой из простых балок:

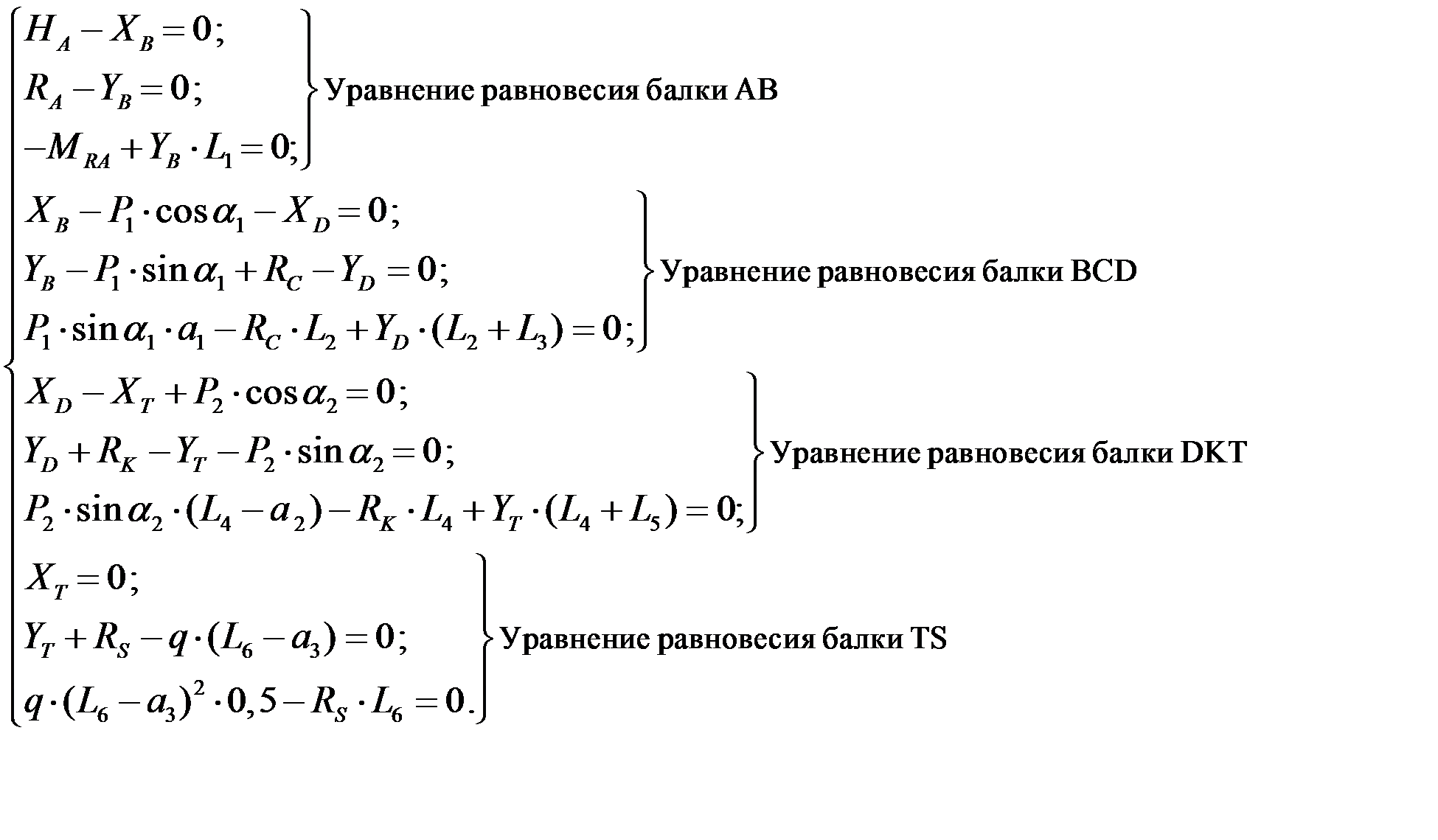Используя MathCAD, решим полученную систему уравнений:

Результат решения задачи, представим в виде эпюр «M», «Q», «N».

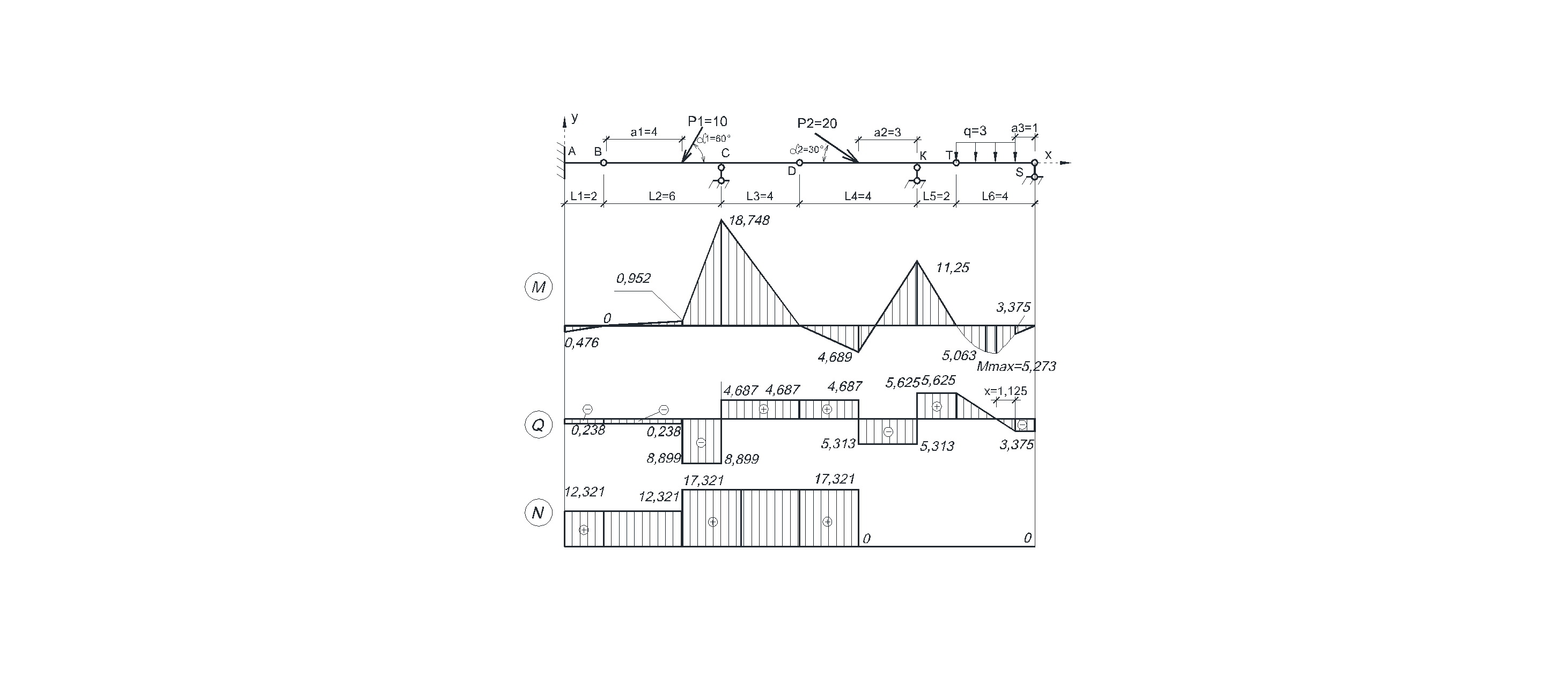Рисунок 2.2 ­ Результаты расчета балки- эпюры «M», «Q», «N»

Проверим достоверность результатов, используя программный комплекс LiraSAPR2013 и SCAD.