Просчитайте все возможные варианты и определите наилучший вариант решения.
Вариант 1 .
Центр Компьютерного Тренинга готовит сертифицированных специалистов Майкрософт MCSE 2000. Особенностью Центра является то, что он гарантирует трудоустройство каждому слушателю, успешно закончившему курсы в течение одного месяца после окончания. Как правило возможностью получить работу по рекомендации Центра пользуются около 70% слушателей, остальные удовлетворяются продвижением в своей компании. Если слушатель, желающий получить новую работу, не получает ее в течение одного месяца, ему возвращается полная стоимость обучения - $1500.
Плановая прибыль с каждого выпускника около $1000. Так как Центр делает 10 выпусков в год, имеется неплохая статистика работы, используя которую менеджер Центра оценил вероятности поступления разных количеств заявок на подготовленных специалистов в следующем месяце:
Таблица – Вероятности поступления заявок
| Спрос, человек | 7-11 | 12-16 | 17-19 | 20-22 | 23-25 | 26-30 |
| Вероятность | 0.09 | 0.14 | 0.23 | 0.27 | 0.22 | 0.05 |
Кроме вероятностей реализации различных значений спросов, менеджер подсчитал и точность полученных значений. По этим данным он сделал вывод о том, что (из-за ошибок оценки) вероятности реализации не должны быть хуже и не должны быть лучше чем представленные во второй таблице.
Таблица – Оценки вероятностей реализации
| Спрос, человек | 7-11 | 12-16 | 17-19 | 20-22 | 23-25 | 26-30 |
| Не хуже чем | 0.15 | 0.19 | 0.25 | 0.24 | 0.16 | 0.01 |
| Не лучше чем | 0.04 | 0.11 | 0.21 | 0.28 | 0.26 | 0.1 |
По этим данным требуется оценить оптимальный размер набираемой группы и ожидаемую прибыль.
a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков)
b. Какой величины класс нужно формировать школе, чтобы максимизировать прибыль?
c. Независимая служба маркетинговых исследований предлагает сделать прогноз спроса на специалистов, выпускаемых школой. Стоимость исследования $3000. Воспользовались ли бы Вы таким предложением, будь Вы на месте менеджера школы. Ответ обоснуйте количественно.
Вариант 2.
Фирма, занимающаяся оптовой торговлей хозяйственными товарами, планирует закупки снеговых лопат к предстоящему сезону. Каждая лопата, являющаяся качественным инструментом, стоит 150 руб. в закупке и может быть продана в сезон за 250 руб. в нормальную по снежности зиму. В умеренную зиму прибыль уменьшается на 20 руб. а в снежную зиму – возрастает на 20 руб. Так как остатки, нераспроданные в сезон, невыгодно держать до следующего года, вследствие значительных издержек хранения и неоправданного увеличения складской площади, они распродаются в начале марта по цене 80 руб. в обычную зиму, по цене 60 руб. в умеренную и по 100 руб. в снежную.
Данные прошлых лет указывают, что продажи лопат сильно зависят от снежности зимы и для малоснежной, нормальной и сильно снежной зимы могут быть описаны в числах, представленных в следующей таблице. Вероятности разных уровней спроса даны для каждой зимы отдельно.
Таблица – Вероятности уровней спроса
| Снежность | Умеренная зима | Нормальная зима | Снежная зима | ||||||
| Кол-во лопат, тыс. штук | 5 | 6 | 7 | 15 | 18 | 20 | 30 | 35 | 40 |
| Вероятность | 0.20 | 0.50 | 0.30 | 0.35 | 0.45 | 0.20 | 0.40 | 0.50 | 0.10 |
Если закупленных лопат не хватает, фирма может докупить их в сезон по более высокой цене: 210 руб. в нормальный сезон, 170 – в малоснежный и 250 руб. – в снежный, а может и не докупать, оставив неудовлетворенный спрос другим поставщикам. В случае, если спрос не удовлетворен, считаем, что фирма ничего не теряет.
Перед новым зимним сезоном вероятности наступления умеренной, нормальной и снежной зим оцениваются бюро прогнозов по данным статистики как 35% - 40% - 25% соответственно.
a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Сколько лопат нужно закупить, чтобы максимизировать прибыль?
b. Какова будет средняя ожидаемая прибыль при оптимальном количестве закупаемых лопат?
c. Сколько лопат следовало бы закупить, если бы вероятности разных уровней спроса были бы неизвестны? Каким критерием лучше воспользоваться?
d. Специалист бюро прогнозов предлагает улучшить качество прогноза, для чего нужно проделать дополнительные исследования данных зарубежных бюро прогнозов. Он оценивает стоимость такой работы в 50 тыс. руб. Следует ли заказать эту работу?. Ответ обоснуйте количественно.
e. Специалист по результатам работы представил новую оценку вероятностей различной снежности: 20% - 65% - 15% для умеренной, нормальной и снежной зим. Какую прибыль от продажи лопат вы теперь ожидаете получить в предстоящем сезоне?
Вариант 3.
Предприятие производит электротермометры ЭТ-300, которые c вероятностью p могут быть дефектными. Количество изделий в партии 200.
Прошлый опыт указывает, что из-за неустойчивой работы производственной линии p равно либо 0.05, либо 0.10, либо 0.25. Причем, в 70 % произведенных партий, p равняется 0.05, в 20% - p= 0.10, а в 10% партий p равняется 0.25.
ЭТ-300 используются при сборке приборов, и в конечном счете их качество будет определено конечным ОТК. При этом можно или испытывать каждый электротермометр на специальном стенде, что обходится в $8 за штуку и отбрасывать дефектные или использовать его на сборке непосредственно без испытания. Если выбрано последнее, дефект обнаружится при сплошном оконечном контроле, а стоимость переделки составит в конечном счете $90 за каждый прибор.
a. По этим данным постройте матрицу прибылей и рассчитайте ожидаемые затраты на каждую партию. Какое решение следует принять, испытывать электротермометры или нет?
b. Допустим, что из каждой партии можно отправить в лабораторию 10 термометров, и по этой выборке достоверно установить процент бракованных изделий в партии. Стоимость анализа $200. Стоит ли проводить такой анализ? Каковы будут суммарные издержки в этом случае?
Вариант 4.
Менеджер закупочного отдела магазина хозяйственных товаров должен решить, сколько циркулярных пил закупить для продажи в текущем строительном сезоне. Каждая пила покупается у дилера за $60, а продается в магазине за $100.
Каждая непроданная в сезон пила требует серьезных расходов на хранение и в результате приносит убыток $25.
Менеджер может покупать товар у дилера только партиями по 100 штук. Из прошлого опыта известны вероятности продать партии товара различного размера
Таблица – Вероятности продажи товара
| Спрос | 300 | 400 | 500 | 600 | 700 |
| Вероятности | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа циркулярных пил. Какова будет средняя прибыль при каждом из выборов партии?
b. Какой критерий Вы предпочитаете в данной ситуации? Объясните.
c. Независимая служба маркетинговых исследований предлагает сделать прогноз спроса на пилы в районе данного магазина на наступающий сезон. Стоимость исследования $3100. Воспользовались ли бы Вы таким предложением, будь Вы на месте менеджера закупочного отдела? Ответ обоснуйте количественно.
Вариант 5.
Годовой запас ботинок некоторого популярного типа для большого универмага нужно заказывать заранее. Каждая пара стоит $ 30, продается за $ 60, и может быть продана на распродаже только за $ 15, если не будет продана до конца года. Рассматриваются следующие варианты заказа: 20, 30, 40, или 50 пар.
Уровни спроса и их вероятности даны в таблице:
Таблица – Уровни спроса и их вероятности
| Спрос | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Вероятности | 0.20 | 0.25 | 0.20 | 0.15 | 0.10 | 0.05 | 0.05 |
a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Сколько пар ботинок нужно заказывать, чтобы максимизировать ожидаемую прибыль?
b. Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа.
c. Какой критерий Вы предпочитаете в данной ситуации? Объясните.
Вариант 6.
Зеленщица на маленьком рынке в провинциальном городке продает зелень, выращенную в собственной отапливаемой теплице. Свежесрезанная зелень продается в тот же день за 3 рубля. Если часть зелени не продается, ее приходится выбрасывать и зеленщица теряет на этом в среднем по 2 руб за пучок, (издержки по содержанию теплицы). Хозяйка каждый день записывает, сколько десятков пучков зелени ей удалось продать. Записи за последние 3 или 4 месяца можно было бы обобщить следующим образом: 1 день удалось продать только 4 десятка пучков зелени, 4 дня - 5 дес. пучков, 15 дней – 6 дес., 25 – 7 дес., 30 – 8, 23 – 9, 9 – 10, 4 – 11 и 1 день – 12 дес. пучков.
a. Подскажите хозяйке, какое количество пучков зелени нужно срезать к торговому дню, чтобы максимизировать прибыль?
b. Соседка зеленщицы - гадалка, иногда предсказывает ей какое количество зелени нужно приготовить к следующему дню. Гадалка предлагает за 5 рублей за сеанс каждый вечер предсказывать спрос на завтра. Стоит ли зеленщице тратиться на гадалку?
c. Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о количестве подготавливаемой зелени.
Вариант 7.
Маленькая кондитерская в курортном городе продает выпечку собственного производства. Фирменные торты выпекаются каждое утро и продаются по цене $7 (при себестоимости - $3). Если торт не продается в день изготовления, он выбрасывается.
Записи, которые ведет хозяйка, показывают, что за последние 100 дней спрос на эти торты имел следующее распределение.
Таблица – Распределение спроса на торты
| Кол-во проданных тортов | 8 | 9 | 10 | 11 | 12 |
| Кол-во дней | 15 | 25 | 30 | 20 | 10 |
a. Подскажите хозяйке, какое количество тортов нужно выпекать, чтобы максимизировать прибыль?
b. Хозяйка водит дружбу с гадалкой, которая каждый вечер предсказывает ей какое количество тортов нужно выпекать на следующий день и берет за услугу $2. Стоит ли хозяйке тратиться на гадалку?
c. Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о партии тортов.
Вариант 8.
Компьютерная школа проводит курсы по подготовке специалистов по обслуживанию компьютерных сетей. Школа гарантирует трудоустройство каждому слушателю, успешно закончившему курсы в течении недели. В противном случае школа возвращает слушателю всю стоимость обучения ($2000).
С каждого трудоустроенного выпускника школа имеет прибыль - $1000. Из предыдущего опыта и из анализа объявлений о приглашении на работу квалифицированных специалистов по компьютерным сетям менеджер школы оценил вероятность трудоустройства подготовленных специалистов для типичной недели.
Таблица – Оценка вероятностей трудоустройства специалистов
| Средние продажи | 10 | 11 | 12 | 13 | 14 | 15 |
| Случаев | 0.1 | 0.2 | 0.25 | 0.25 | 0.15 | 0.05 |
a. Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков)
b. Какой величины класс нужно формировать школе, чтобы максимизировать прибыль?
c. Какова будет средняя прибыль при оптимальном размере класса?
d. Используйте критерии максимина, минимаксного риска для принятия решения о величине класса.
e. Независимая служба маркетинговых исследований предлагает сделать прогноз спроса на специалистов, выпускаемых школой. Стоимость исследования $1300. Воспользовались ли бы Вы таким предложением, будь Вы на месте менеджера школы. Ответ обоснуйте количественно.
Вариант 9.
Производитель изготавливает и продает некоторое изделие А в полных лотах по 50 единиц каждый. Эти изделия имеют очень ограниченный срок годности; поэтому, если они сделаны, но не проданы, то их приходится выбрасывать. Если же спрос превышает запланированную партию, то недостающий товар обязательно необходимо произвести в сверхурочное время.
Стоимость единицы изделия при нормальном производственном цикле равна 5 $. Стоимость дополнительного производства равна 7 $ за единицу. Все изделия продаются по цене 10 $ за единицу, независимо от стоимости производства.
Исторически спрос составлял 50, 100 либо 150 единиц в неделю, так что компания делает один, два или три лота. В прошлом менеджер отдела постоянно заказывал изготовление 100 единиц в неделю.
a. Составьте матрицу выигрышей и потерь и рассчитайте прибыли для каждого из размеров партии.
b. Если вероятность спроса в 50 единиц в неделю равна 40%, вероятность спроса в 100 единиц – 50%, и вероятность спроса в 150 единиц – 10%, какой размер партии Вы рекомендовали бы, если цель состоит в том, чтобы максимизировать ожидаемую прибыль?
c. Для постоянной переоценки спроса на следующую неделю может быть нанят специалист по маркетингу. Его заработок составит 100 $ в неделю. Стоит ли нанимать его?
d. Ответьте на те же вопросы a), b), и c), учитывая теперь, что непроданные изделия приходится утилизировать, что обходится в 1$ за единицу.
Вариант 10.
Компания «Супермаски» продает маски Halloween в киосках в местном парке. Магазинчики открыты в течение октября месяца. Маски стоят магазину $ 3.45 каждая; они продаются в розницу по $9.95. Любая маска, не купленная вовремя, после праздника продается специалисту по распродаже товаров по цене $1.80.
Результаты продаж за последние 3 года в 10 киосках компании сведены в таблицу.
Таблица – Результаты продаж за 3 года
| Средние продажи | 750 | 800 | 850 | 900 | 950 | 1000 | 1050 | 1100 |
| Случаев | 1 | 4 | 9 | 6 | 4 | 3 | 2 | 1 |
Поскольку маски импортированы из Азии, заказ должен быть размещен в мае, последующее изменение заказа невозможно.
a. Постройте таблицу выигрышей и потерь. Подсчитайте вероятности различных уровней спроса.
b. Какой заказ (в расчете на 1 киоск) максимизирует среднюю ожидаемую прибыль?
c. Какова будет прибыль, если стоимость арендной платы, труда, страхования и прочие издержки по использованию киоска – приблизительно $ 3000 за сезон продаж?
Задание 4.
Построение дерева решений
Вариант 1
Компания «ОбувьСити», управляющая сетью магазинов готовится к закупкам обуви на предстоящий осенний сезон. Основную долю в продажах в это время года дают полусапоги, ботинки и осенние туфли. Отдел продаж планирует продать за сезон 1 млн. пар женской обуви. У директора отдела имеются три оценки спроса в конкретных позициях, рассчитанные для различных погодных условий. Если осень будет сухая, то сеть магазинов сможет реализовать примерно 200 тыс. пар полусапог, 500 тыс. пар ботинок и 300 тыс. пар туфель. Если осень будет очень сырая, то можно ожидать продажи примерно 600 тыс. пар полусапог, 300 тыс. пар ботинок и 100 тыс. пар туфель. При средних погодных условиях, не отличающихся ни излишней влажностью, ни малым количеством осадков, можно ожидать продажи около 300 тыс. пар полусапог, 500 тыс. пар ботинок и 200 тыс. пар туфель. Требуется решить, на какой сценарий спроса ориентироваться при закупках.
Статистические данные для региона, в котором работает компания, свидетельствуют о том, что сырая осень наблюдается в 1 году из 10, «средние» погодные условия случаются в 3-х годах из 10, а сухая осень бывает 6 лет из 10 в среднем. Так как закупки планируются за 6 месяцев, то реально использовать метеопрогноз невозможно.
Пара полусапог, проданная в сезон, приносит компании $20 прибыли, а оставшаяся до следующего сезона ведет к убыткам в $2, в результате выплат по кредиту, взятому по закупки. Для ботинок прибыли и убытки составят $15 и $1.5, а для туфель – $10 и $1.
a. Какой из трех разработанных планов закупки принять директору отдела закупок, если исходить из максимума ожидаемой прибыли? Какую валовую прибыль при этом можно ожидать по результатам сезона в этих трех позициях обуви?
b. Управляющий отделом стратегического анализа утверждает, что погода в последние несколько лет не соответствует средним оценкам. Как изменились вероятности тех или иных погодных условий он сказать не может. Повлияет ли это обстоятельство на принятое вами решение? Какую прибыль можно ожидать при отсутствии данных о вероятностях различных погодных сценариев?
c. Финансовый директор требует, чтобы его не вводили в заблуждение излишне оптимистичными оценками денежных потоков от реализации. Она предлагает отделу закупок рассчитывать на самые неблагоприятные условия. Какую прибыль можно ожидать в среднем при наилучшем выборе для этих условий?
Вариант 2
Вы владеете неразработанным золотым рудником, стоимость разработки которого составляет 100 000 дол. Вы предполагаете, что если начнете разработку рудника, то сможете добывать ежегодно по 1000 унций золота в течение 3 лет. На этом все запасы золота будут исчерпаны.
В настоящее время цена золота составляет 500 дол. за унцию. В целом в долгосрочной перспективе цена золота растет, однако на этом фоне имеются колебания в цене. Вероятность того, что за следующий год цена золота вырастет на 50 дол. от уровня цены в начале года примерно равна 37%, вероятность того, что цена упадет на 50 дол. – 30%, и с вероятностью 33% цена золота в конце года останется на прежнем уровне.
Эксплуатационные издержки составляют 420 дол. на унцию. Ставка дисконта равна 10%.
Необходимо решить, разрабатывать рудник, или нет.
- Постройте "древо решений", иллюстрирующее эти варианты и охватывающее 3 года.
- Следует ли вам начать добычу золота сейчас или подождать, надеясь, что цена на золото вырастет?
- Как бы повлиял на ваше решение тот факт, что вы могли бы без ущерба (но окончательно) прекратить добычу на любом этапе?
Вариант 3
Владелец небольшой риэлторской фирмы г. Сидоров получил горящее предложение о покупке трех квартир. Квартиры продавались за общую сумму 720 тыс. $ и только все вместе. Так как у фирмы имелась довольно приличная база данных по сделкам на покупку-продажу квартир в городе, он достаточно быстро смог оценить перспективы продажи. У него получились при этом следующие оценки:
Квартира А - будет продана за $ 270 000
Квартира Б – 20 шансов из 100 продать за 250 тыс. $; 60% - 260 тыс. $; и 20% вероятности продать за 280 тыс. $
Квартира В - 30 % - 250 тыс. $; 50% - 270 тыс. $ и 20% - 300 тыс. $.
При этом квартира будет продана первому клиенту, готовому заплатить цену не меньшую нижней границы цен.
Общие расходы по продаже (предпродажная подготовка, оформление документов и пр.) должны составить около 10,000 $ за каждую квартиру.
Бизнесмен надеется продать эти объекты за 2 месяца, но у него сейчас (и в трехмесячной перспективе) практически нет свободных денег. Он имеет только 50 тыс. $, которые можно вложить в эту сделку. Т.о. он будет вынужден взять кредит в размере 700 000 $ на срок два месяца. Условия по кредиту довольно жесткие – возвращения кредита ждут не позже и не раньше чем через 2 месяца, при этом процент по кредиту составит 4% за два месяца. Если возвращение кредита затянется на 3 месяца, то придется выплатить в общей сложности 7%.
Он полагает, что квартира А будет наверняка продана в течение месяца. А для квартиры Б (как и для В) вероятность продажи в первом месяце составит 30%.
В следующем месяце вероятность продажи квартиры увеличится до 60%. Затем будет месяц, в котором рынок недвижимости традиционно оживляется, и все
квартиры будут наверняка проданы.
Среднемесячная норма прибыли у бизнесмена около 5%.
a. Принимать ли г.Сидорову это предложение?
b. Постройте дерево решений. Рассчитайте, сколько денег в среднем вернется к нему в первом, втором и третьем месяцах.
c. Рассчитайте вероятность своевременного возвращения кредита.
Вариант 4
Хозяин пекарни ведет переговоры с муниципалитетом городского района о заключении контракта на поставку продукции в школы этого района и с администрацией предместья на поставку продукции в столовые этого района. После консультаций с экспертами, владелец оценивает вероятности заключения контрактов следующим образом
| Результат | Нет контрактов | Контракт с городом | Контракт с предместьем | Оба контракта |
| Вероятность | 0,2 | 0,2 | 0,5 | 0,1 |
Хозяин имеет возможность купить подержанный грузовик по хорошей цене, что может понадобиться для предполагаемых контрактов. Если хозяин не будет покупать грузовик и ни один контракт не будет заключен, прибыль равна нулю. Если будет заключен контракт с городом будет получена прибыль $14,000 (за счет внутренних ресурсов фирмы). Если будет заключен контракт с предместьями прибыль составит $10,000. Если будут заключены оба контракта, использовать дополнительный грузовик будет абсолютно необходимо. Аренда грузовика обеспечит суммарную прибыль $8,000.
Хозяин может принять решение о покупке грузовика. При этом если сохранится возможность покупки подержанного грузовика (вероятность - 0.3), прибыль составит $16,000. Если придется покупать новый грузовик прибыль составит всего $6,000.
Если хозяин купит немедленно подержанный грузовик, оба контракта будут заключены, прибыль (как уже сказано) составит $16,000. Если будет заключен контракт с городом прибыль составит $8000. При заключении контракта с предместьями прибыль составит $9000. Если ни один контракт не будет заключен, хозяин потерпит убытки в $6000. Однако если удачно продать грузовик ( вероятность 0.6) можно получить прибыль $2000.
a. Покупать или не покупать грузовик до заключения контрактов?
b. Начертите дерево решений и примите решение на основании ожидаемой величины прибыли.
Вариант 5
Родители хотят подарить дочери ко дню свадьбы квартиру. Они предполагают, что свадьба будет не ранее, чем через 9 лет. В настоящий момент их сбережения составляют только 15 тыс. долл. Поскольку увеличить эти сбережения за счет их трудовой деятельности представляется проблематичным, родители рассматривают различные варианты инвестирования имеющихся средств.
Вариант 1 – купить комнату в коммунальной квартире. Сейчас такая комната стоит 15 тыс. долл. Если ее сдавать, можно получить прибыль примерно 100 долл. в месяц. За 9 лет это составит (без учета инфляции) 10 тыс. 800 долл., после чего комнату можно продать по нынешним оценкам за 13 тыс. долл. При этом существует возможность того, что коммунальную квартиру расселят или московское правительство решит снести дом и предоставит жителям коммуналки отдельные квартиры. Можно считать, что такая возможность представится через 6 лет и вероятность ее не выше 20%. Оценим однокомнатную квартиру в 40 тыс. долл.
Вариант 2 – положить деньги в банк на срочный вклад под 7,5% годовых.
Однако, родители, пережив многочисленные потрясения, не верят в стабильность экономической ситуации в России и оценивают потерю всех денег с вероятностью 50%.
Вариант 3 – купить квартиру у одинокого пенсионера с условием выплаты пожизненной ренты. Есть предложение купить квартиру за $11000 + $400 пожизненной ренты каждый год. Родители оценивают вероятность выплат в течение 9 лет как 10%; 7 лет – как 20%; 5 лет – как 50%. Кроме того, вероятность того, что у одинокого пенсионера найдутся наследники, которые добьются признания сделки недействительной после его смерти, оценивается как 20%.
Какой из вариантов лучше?
Вариант 6
Компания "Обуем всех" предполагает заменить старую машину по пошиву обуви на более современное оборудование. Новое оборудование стоит $10 млн, и компания предполагает продать свою старую машину за $1 млн. Привлекательность новой машины в том, что благодаря ее применению ожидается снижение производственных издержек с $8 на пару до $4. Однако, как показано в приведенной ниже таблице, существует некоторая неопределенность относительно и будущего объема продаж, и эксплуатационных характеристик новой машины:
| Пессимистичные р=1/3 | Ожидаемые р=1/3 | Оптимистичные р=1/3 | |
| Продажи (тыс. пар) | 400 | 500 | 700 |
| Производственные издержки с новой машины ($/пара) | 6 | 4 | 3 |
| Срок службы новой машины (лет) | 7 | 10 | 13 |
Причем все три возможности равновероятны. Учтите, что параметры продажи, срок службы и производственные издержки независимы друг от друга – т.е. при издержках, соответствующих, например, оптимистичному прогнозу, срок службы и уровень продаж могут быть любыми, скажем 7 лет и 500 тыс. и т.д.
a. Начертите дерево решений и примите наилучшее решение – покупать машину или нет?
b. Какова ожидаемая величина прибыли? Учтите, что ставка дисконта равна 12%. Отпускная цена пары обуви 10$; "Обуем всех" нагло не платит налогов (т.е. дополнительные издержки не следует учитывать).
Вариант 7
Управляющий производственным отделом корейской компании, производящей жидкокристаллические панели для мониторов анализирует возможности модернизации цеха.
Дешевый план предполагает вложение 10 млн. долл. При этом ожидается, что новое оборудование с вероятностью 90% позволит получать 70%-ный выход годных панелей и с вероятностью 10% - даже 80% -ный.
Дорогой план предполагает вложение 15 млн. долл. При этом более совершенное оборудование позволит иметь 70%-ный выход годных панелей с вероятностью 30%. Иначе выход годных трубок достигнет 77%.
Планируется произвести 1 млн. качественных панелей до следующей модернизации оборудования.
Себестоимость панелей составит во всех случаях 110 долл. Средняя рыночная цена на такие панели с учетом постепенного удешевления составит 200 долл..
a. Какое решение, А или В, Вы порекомендовали бы принять? Какова ожидаемая прибыль?
b. Представьте, что в случаях, когда выход качественных панелей составляет только 70% можно отобрать еще 5% от общего их числа для коррекции. Дополнительная коррекция стоимостью $50 на каждую панель даст дополнительные 5% пригодных панелей (т.о. общий выход составит 75%). Нарисуйте дерево решений и рассчитайте, какое решение было бы разумно принять в этом случае. Как изменится
ожидаемая прибыль?
Вариант 8
Сотрудник одного из Министерств, достигнувший 40-летнего возраста, стоит перед выбором одной из трех альтернатив и для продолжения трудовой деятельности у нег есть возможность а) пройти 2-х летнее вечернее обучение в Институте А, за которое необходимо оплатить по 5000 у.е. в начале каждого учебного года; б) пройти 3-х летнее вечернее обучение в Университете Б, за которое необходимо оплатить по 2000 у.е. в начале каждого учебного года; в) не повышать квалификацию и продолжать работать, пытаясь найти хорошо оплачиваемую должность. В случае отказа от учебы чиновник оценивает свои шансы удачно занять должность с годовым доходом 13200 у.е. как 10 к 90. В противном случае в течение ближайших 13 лет он будет занимать должность с годовым доходом 7200 у.е.
По сведениям, полученным в деканате А, во время 1-ого года обучения 20-ти процентам обучающихся удается найти работу со средним годовым доходом 9600 у.е., а 80-ти процентам - со средним доходом 4800 у.е. Во время 2-ого года обучения этим двум группам удается увеличить годовой доход до 14400 у.е. и 6000 у.е. соотв-но. После окончания А группе с доходом 14400 у.е. с 80%-ой вероятностью предлагаются места с годовым доходом 24000 у.е., который удается сохранить как минимум на 11 лет. Остальные 20% из них имеют среднегодовой доход 14400 у.е. на ту же перспективу. Тем же выпускникам А, кто получал доход 6000 у.е., с 70%-ой вероятностью удается увеличить годовой доход до 24000 у.е. и далее сохранить его как минимум на 11 лет. В противном случае их вероятный среднегодовой доход на этот же период - 14400 у.е.
Статистика доходов обучающихся и выпускников Б свидетельствует о следующем. 20% обучающихся имеют среднегодовой доход 9600, 10800 и 12000 у.е. в 1-й, 2-й и 3-й годы обучения соответственно. При этом 60% из них после выпуска имеют совокупный (за 10 лет) доход 180000 у.е., а 40% - 120000 у.е. 80% обучающихся имеют среднегодовой доход 4800, 6000 и 7200 в 1-й, 2-й и 3-й годы обучения соответственно. При этом 60% из них после выпуска имеют совокупный (за 10 лет) доход 120000 у.е., а 40% - 72000 у.е.
a. Какая из трех альтернатив будет более выгодна для сотрудника, если он хочет принять решение по критерию максимальной прибыли, которая может быть им получена за ближайшие 13 лет?
b. Является ли решение устойчивым при существенном снижении прогнозируемых годовых доходов выпускника А или при значительном снижении вероятности получения удачного варианта дохода выпускником А?
Вариант 9
Небольшая компания, занимающаяся разработкой новых средств бытовой химии, управляет биохимической лабораторией. Недавно сотрудники лаборатории нашли новое интересное решение для средства чистки ковровых покрытий. Потенциально это средство может принести весьма значительные прибыли, но компания не имеет достаточных финансовых ресурсов, для того, чтобы вывести это средство на рынок так, чтобы полностью реализовать его рыночный потенциал.
Президент компании рассматривает следующие три возможности.
Довести исследования до конца и попытаться вывести средство на рынок за счет собственных средств. Это потребует $2 млн инвестиций в разработку конечного продукта и $500 тыс. на продвижение средства на рынок. Такие средства у компании имеются. Однако в этом случае дальнейшая рыночная история средства будет сильно зависеть от действий крупных компаний. Анализ рыночной ситуации показывает, что наиболее вероятно (65%) получение в течение следующего года $12 млн. валового дохода от продаж. При менее благоприятных обстоятельствах компания получит не более $6 млн. (вероятность этого 25%). И, наконец, в случае высокой активности в этом сегменте рынка других компаний (вероятность 10%), будет получено только $2 млн. Дальше чем на год аналитики предпочитают не заглядывать, так как неопределенность оценок становится слишком велика.
Продать свои разработки крупной компании. Это не потребует никаких инвестиций и может принести в среднем $5 млн.
Найти необходимые средства у стороннего инвестора и профинансироватьпрограмму исследований и продвижение средства на рынок в полном объеме. Для этого потребуется $5.5 млн на разработку конечного продукта и $9 млн. на продвижение средства на рынок. Таким образом $12 млн. вложит в дело инвестор.
При этом прибыли (после компенсации издержек) придется делить пополам. В этом случае с вероятностью 50% от продажи средства за тот же период будет получено $35 млн. В более сложной ситуации, вероятность которой оценивается в 25%, можно будет получить только $25 млн. И в худшем случае будет получено только $15 млн.
- Постройте дерево решений и определите величину ожидаемых доходов в каждом случае.
- Какое решение вы считаете лучшим? Обоснуйте свой ответ.
- Исследуйте устойчивость решения при варьировании соотношения вероятностей лучшего и худшего исходов.
Вариант 1 0
Президент компании рассматривает два решения для новой линии по производству электронно-лучевых трубок для компьютерных рабочих станций. Продажи ЭЛТ в течение жизненного цикла прогнозируются в размере 150 000 штук.
Решение А имеет вероятность 80% производства 59 хороших ЭЛТ из 100 и вероятность 20% производства 64 хороших ЭЛТ из 100. Это решение будет требовать начальных вложений 1 млн. долл.
Решение В имеет вероятность 60% производства 64 хороших ЭЛТ из 100 и вероятность 40% производства 59 хороших изделий из 100. Это решение будет требовать затрат 1.4 млн. долл.
Хорошая или плохая, каждая трубка будет иметь себестоимость $80. Каждое качественное изделие будет продано за $145. Какое решение, А или В, вы порекомендовали бы принять? Какова ожидаемая прибыль?
Представьте, что в случаях, когда выход качественных трубок составляет только 59% можно отобрать еще 10% трубок (от общего их количества) для коррекции. Дополнительная коррекция стоимостью $40 на каждую трубку даст дополнительные 7% пригодных трубок (т.о. общий выход составит 66%).
Нарисуйте дерево решений и рассчитайте, какое решение было бы разумно принять в этом случае. Как изменится ожидаемая прибыль, по сравнению с первым вариантом?
Задание 5.
Принятие решений в условиях неопределенности.Игры с природой
Методические указания
Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игрок1. Игрок 2 (природа) сознательно против игрока 1 не действует, а выступает как не имеющий конкретной цели и случайным образом выбирающий очередные «ходы» партнер по игре. Поэтому термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально.
Матрица игры с природой А = ||аij||, где аij – выигрыш (потеря) игрока 1 при реализации его чистой стратегии i и чистой стратегии j игрока 2 (i=1, …, m; j=1,…,n).
Мажорирование стратегий в игре с природой имеет определенную специфику: исключать из рассмотрения можно лишь доминируемые стратегии игрока 1: если для всех g=1,…, n akj alj, k, l = 1,…,m, то k-ю стратегию принимающего решения игрока 1 можно не рассматривать и вычеркнуть из матрицы игры. Столбцы, отвечающие стратегиям природы, вычеркивать из матрицы игры (исключать из рассмотрения) недопустимо, поскольку природа не стремится к выигрышу в игре с человеком, для нее нет целенаправленно выигрышных или проигрышных стратегий, она дей ствует неосознанно.
Рассмотрим организацию и аналитическое представление игры с природой. Пусть игрок 1 имеет m возможных стратегий: А1,А2, … , Аm, а у природы имеется n возможных состояний (стратегий): П1, П2, ..., Пn, тогда условия игры с природой задаются матрицей А выигрышей (потерь) игрока 1:
| П1 | П2 | … | Пn | |
| A1 | a11 | a12 | a1n | |
| A2 | a21 | a22 | a2n | |
| … | ||||
| Am | am1 | am2 | amn |
Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей (потерь), а в виде так называемой матрицы рисков R = ||rij||m,n. Величина риска - это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей (потерь) А.
Риск - это разность между результатом, который игрок мог бы получить, если бы он знал действительное состоянием среды и результатом, который игрок получит при j-ой стратегии.
Зная состояние природы (стратегию) Пj, игрок выбирает ту стратегию, при которой его выигрыш максимальный или потеря минимальна, т.е.
rij = j-aij, где j = max aij, при заданном j, i=1,…, m, если аij – выигрыш;
rij = aij - j, где j = min aij, при заданном j, i=1,…, m, если аij – потери (затраты).
Неопределенность, связанную с полным отсутствием информации о вероятностях состояний среды (природы), называют «безнадежной».
В таких случаях для определения наилучших решений используются следующие критерии: Вальда, Сэвиджа, Гурвица.
Критерий Вальда. С позиций данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник.
Если в исходной матрице по условию задачи результат aij представляет выигрыш лица, принимающего решение, то выбирается решение, для которого достигается значение W = max min aij, i=1,…, m, j=1,…, n – максиминный критерий.
Если в исходной матрице по условию задачи результат aij представляет потери лица, принимающего решение, то выбирается решение, для которого достигается значение W = min max aij, i=1,…, m, j=1,…, n – минимаксный критерий.
В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучшей. Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай.
Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей А, а матрицей рисков R:
S = min max rij , i=1,…, m, j=1,…, n.
Применение критерия Сэвиджа позволяет любыми путями избежать большого риска при выборе стратегии, а значит, избежать большего проигрыша (потерь).
Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом.
Критерий основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятность (1-р) и в самом выгодном состоянии с вероятностью р, где р – коэффициент пессимизма.
Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением:
HA = max p max aij + (1-p) min aij , i=1,…, m, j=1,…, n, если aij – выигрыш;
HA = min p min aij + (1-p) max aij , i=1,…, m, j=1,…, n, если aij – потери (затраты).
При p = 0 критерий Гурвица совпадает с критерием Вальда. При p = 1 приходим к решающему правилу вида max max aij, к так называемой стратегии «здорового оптимизма», критерий максимакса.
Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид:
HR = min p max rij + (1-p) min rij , i=1,…, m, j=1,…, n.
При р = 0 выбор стратегии игрока 1 осуществляется по условию наименьшего из всех возможных рисков (min rij); при р = 1 – по критерию минимаксного риска Сэвиджа.
Значение р от 0 до 1 может определяться в зависимости от склонности лица, принимающего решение, к пессимизму или оптимизму. При отсутствии ярко выраженной склонности р = 0,5 представляет наиболее разумный вариант.
В случае, когда по принятому критерию рекомендуются к использованию несколько стратегий, выбор между ними может делаться по дополнительному критерию. Здесь нет стандартного подхода. Выбор может зависеть от склонности к риску игрока1.
Пример
Транспортное предприятие должно определить уровень своих производственных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но прогнозируется, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия. Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Возможные прогнозируемые затраты на развитие провозных возможностей представлены в табл.
Таблица 6
| Варианты провозных возможностей транспортного предприятия | Варианты спроса на транспортные услуги | |||
| 1 | 2 | 3 | 4 | |
| 1 | 6 | 12 | 20 | 24 |
| 2 | 9 | 7 | 9 | 28 |
| 3 | 23 | 18 | 15 | 19 |
| 4 | 27 | 24 | 21 | 15 |
Необходимо выбрать оптимальную стратегию. Использовать: критерий Вальда, критерий Сэвиджа, критерий Гурвица.
Решение
| А = |
Имеются четыре варианта спроса на транспортные услуги, что равнозначно наличию четырех состояний «природы»: П1, П2, П3, П4. Известны так же четыре стратегии развития провозных возможностей транспортного предприятия: А1, А2, А3, А4. Затраты на развитие провозных возможностей при каждой паре Пi и Аi заданы следующей матрицей:
| П1 | П2 | П3 | П 4 | |
| А1 | 6 | 12 | 20 | 24 |
| А2 | 9 | 7 | 9 | 28 |
| А3 | 23 | 18 | 15 | 19 |
| А4 | 27 | 24 | 21 | 15 |
Построим матрицу рисков. В данном примере aij представляет затраты т.е. потери значит для построения матрицы рисков используется принцип rij = aij -β j, гдеβ j = min aij.
Для П1: βj = 6
Для П2:βj = 7
Для П3: βj = 9
Для П4: βj = 15
| R = |
Матрица рисков имеет следующий вид:
| П1 | П2 | П3 | П4 | |
| A1 | 0 | 5 | 11 | 9 |
| A2 | 3 | 0 | 0 | 13 |
| А3 | 17 | 11 | 6 | 4 |
| А4 | 21 | 17 | 12 | 0 |
Критерий Вальда
Так как в данном примере aij представляет затраты т.е. потери, то применятся минимаксный критерий.
Для А1: max aij = 24
Для А2: max aij = 28
Для А3: max aij = 23
Для А4: max aij = 27
W = min max aij = 23 наилучшей стратегией развития провозных возможностей в соответствии с минимаксным критерием Вальда будет третья стратегия (А3).
Критерий минимаксного риска Сэвиджа
Для А1: max rij = 11
Для А2: max rij = 13
Для А3: max rij = 17
Для А4: max rij = 21
S = min max rij = 11 наилучшей стратегией развития провозных возможностей в соответствии с критерием Сэвиджа будет первая стратегия (А1).
Критерий пессимизма-оптимизма Гурвица
Положим значение коэффициента пессимизма р = 0,5.
Так как в данном примере aij представляет затраты (потери), то применятся критерий:
HA = min p {min aij + (1-p) max aij}
| min aij | max aij | p min aij + (1-p) max aij | |
| Для А1 | 6 | 24 | 15 |
| Для А2 | 7 | 28 | 17,5 |
| Для А3 | 15 | 23 | 19 |
| Для А4 | 15 | 27 | 21 |
|
|
Оптимальное решение заключается в выборе стратегии А1.
Рассчитаем оптимальную стратегию применительно к матрице рисков
HR = min{ p max rij + (1-p) min rij}
| min rij | max rij | p max rij + (1-p) min rij | |
| Для А1 | 0 | 11 | 5,5 |
| Для А2 | 0 | 13 | 6,5 |
| Для А3 | 4 | 17 | 10,5 |
|
|
Оптимальное решение заключается в выборе стратегии А1.
Вывод: в примере предстоит сделать выбор, какое из возможных решений предпочтительнее:
• по критерию Вальда - выбор стратегии АЗ;
• по критерию Сэвиджа - выбор стратегии А1;
• по критериюГурвица - выбор стратегии А1.
Варианты заданий
Задание 6.
Вариант 1.
Пекарня печет хлеб на продажу магазинам. Себестоимость одной булки составляет 30 пенсов, ее продают за 40 пенсов. В таблице 30 приведены данные о спросе за последние 50 дней:
Таблица – Данные о спросе за 50 дней
| Спрос в день, тыс. шт. | 10 | 12 | 14 | 16 | 18 |
| Число дней | 5 | 10 | 15 | 15 | 5 |
Если булка испечена, но не продана, то убытки составят 20 пенсов за штуку. Используя критерии Вальда, Сэвиджа, Гурвица (при коэффициентах: 0,4- вероятность максимальной покупки, 0,6 – вероятность минимальной покупки), определите, сколько булок нужно выпекать в день.
Вариант 2 .
Дана матрица игры с природой в условиях полной неопределенности (элементы матрицы - выигрыши):
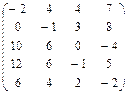
Требуется: проанализировать оптимальные стратегии игрока, используя критерии пессимизма-оптимизма Гурвица применительно к платежной матрице А и матрице рисков R при коэффициенте пессимизма р = 0; 0,5; 1. При этом выделить критерии максимакса, Вальда и Сэвиджа.
Вариант 3.
Компания выбирает, какой вид продукции целесообразно производить. Имеются четыре вида продукции Аj. Определена прибыль от производства каждого вида продукции в зависимости от состояний экономической среды Вi. Значения прибыли для различных видов продукции и состояний природы приведены в таблице 31.
Таблица – Значения прибыли по видам продукции
| Вид продукции | Состояние экономической среды | ||
| В1 | В2 | В3 | |
| А1 | 40 | 52 | 45 |
| А2 | 58 | 45 | 89 |
| А3 | 45 | 36 | 65 |
| А4 | 36 | 89 | 45 |
Требуется выбрать лучший проект легкового автомобиля для производства, используя критерии Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,4. Сравнить решения и сделать выводы.
Вариант 4 .
Один из пяти станков должен быть выбран для изготовления партии изделий, размер которой Q может принимать три значения: 150, 200, 350. Производственные затраты Сi для I станка задаются следующей формулой:
Ci = Pi + ci*Q
Данные Pi и ci приведены в таблице 32.
Таблица – Производственные затраты
|
Показатели | Модель станка | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Pi | 30 | 80 | 50 | 160 | 100 |
| ci | 14 | 6 | 10 | 5 | 4 |
Решите задачу для каждого из следующих критериев Вальда, Сэвиджа, Гурвица (критерий пессимизма равен 0,6). Полученные решения сравните.
Вариант 5 .
При выборе стратегии Aj по каждому возможному состоянию природы Si соответствует один результат Vij. Элементы Vij являющиеся мерой потерь при принятии решения, приведены в таблице33.
Таблица– Меры потерь при принятии решений
|
Стратегии | Состояние природы | |||
| S1 | S2 | S3 | S4 | |
| A1 | 2 | 6 | 5 | 8 |
| A2 | 3 | 9 | 1 | 4 |
| A3 | 5 | 1 | 6 | 2 |
Выберите оптимальное решение в соответствии с критериями Вальда, Сэвиджа, Гурвица (при коэффициенте пессимизма равном 0,5).
Вариант 6 .
Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля Рj. Определена экономическая эффективность Vji каждого проекта в зависимости от рентабельности производства. По истечении трех сроков Si рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в таблице 34.
Таблица – Значения экономической эффективности
| Проекты | Состояние природы | ||
| S1 | S2 | S3 | |
| Р1 | 20 | 25 | 15 |
| Р2 | 25 | 24 | 10 |
| Р3 | 15 | 28 | 12 |
| Р4 | 9 | 30 | 20 |
Требуется выбрать лучший проект легкового автомобиля для производства, используя критерий Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,1. Сравнить решения и сделать выводы.
Вариант 7 .
Определите тип электростанции, которую необходимо построить для удовлетворения энергетических потребностей комплекса крупных промышленных предприятий. Множество возможных стратегий в задаче включает следующие параметры:
R1 – сооружается гидростанция;
R2 – сооружается теплостанция;
R3 – сооружается атомная станция.
Экономическая эффективность сооружения электростанции зависит от влияния случайных факторов, образующих множество состояний природы Si.
Результаты расчета экономической эффективности приведены в таблице 35.
Таблица – Результаты расчета экономической эффективности
| Тип станции | Состояние природы | ||||
| S1 | S2 | S3 | S4 | S5 | |
| R1 | 40 | 70 | 30 | 25 | 45 |
| R2 | 60 | 50 | 45 | 20 | 30 |
| R3 | 50 | 30 | 40 | 35 | 60 |
Вариант 8 .
Фирма рассматривает вопрос о строительстве станции технического обслуживания (СТО) автомобилей. Составлена смета расходов на строительство станции с различным количеством обслуживаемых автомобилей, а также рассчитан ожидаемый доход в зависимости от удовлетворения прогнозируемого спроса на предлагаемые услуги СТО (прогнозируемое количество обслуженных автомобилей в действительности). В зависимости от принятого решения – проектного количества обслуживаемых автомобилей в сутки (проект СТО) Rj и величины прогнозируемого спроса на услуги СТО – построена в таблице 36.
Таблица – Ежегодные финансовые результаты (доход д.е.)
| Проекты СТО | Прогнозируемая величина удовлетворяемости спроса | |||||
| 0 | 10 | 20 | 30 | 40 | 50 | |
| 20 | -120 | 60 | 240 | 250 | 250 | 250 |
| 30 | -160 | 15 | 190 | 380 | 390 | 390 |
| 40 | -210 | -30 | 150 | 330 | 500 | 500 |
| 50 | -270 | -80 | 100 | 280 | 470 | 680 |
Определите наилучший проект СТО с использованием критериев Вальда, Сэвиджа, Гурвица при коэффициенте пессимизма 0,5.
Вариант 9 .
Магазин может завести один из трех типов товара Аi; их реализация и прибыль магазина зависит от типа товара и состояния спроса. Предполагается, что спрос может иметь три состояния Вi. Гарантированная прибыль представлена в матрице прибыли (таб. 37).
Таблица – Гарантированная прибыль от реализации
| Тип товара | Спрос | ||
| В1 | В2 | В3 | |
| А1 | 20 | 15 | 10 |
| А2 | 16 | 12 | 14 |
| А3 | 13 | 18 | 15 |
Определить какой товар закупать магазину.
Вариант 10 .
Администрации театра нужно решить, сколько заказать программок для представлений. Стоимость заказа 200 ф. ст. плюс 30 пенсов за штуку. Программки продаются по 60 пенсов за штуку, и к тому же доход от рекламы составит дополнительные 300 ф. ст. Из прошлого опыта известна посещаемость театра.
Таблица – Вероятности посещаемости театра
| Посещаемость | 4000 | 4500 | 5000 | 5500 | 6000 |
| Ее вероятность | 0,1 | 0,3 | 0,3 | 0,2 | 0,1 |
Ожидается, что 40% зрителей купят программки.
1. Используя критерии Вальда, Сэвиджа и Гурвица, определите, сколько программок должна заказать администрация театра.
2. Допустим, что рекламодатели увеличат сумму с 300 до 400 ф. ст. число посетителей будет больше 5250, к тому же спрос на программки будет полностью удовлетворен. Как это повлияет на рекомендации в п.1?
Задание 6.
Дата: 2019-02-02, просмотров: 2092.