В импульсных устройствах используют импульсы различной формы: прямоугольные, трапецеидальные, экспоненциальные, колоколообразные, ступенчатые и пилообразные (рис. 5, а—е).

Рис.5. Форма видеоимпульсов: а - прямоугольный; б — трапецеидальный; в — экспоненциальный; г — колоколообразный; д — ступенчатый; е — пилообразный

Их называют видеоимпульсами в отличие от радиоимпульсов, представляющих собой пакеты высокочастотных колебаний:

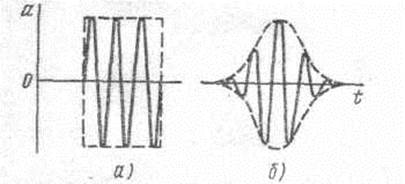
Рис.6. Форма радиоимпульсов: а — прямоугольный; б — колоколообразный

В импульсной технике применяют, как правило, видеоимпульсы.

Обычно импульсы следуют периодически с периодом Т, которому соответствует частота повторения F = 1/Т (рис. 7).

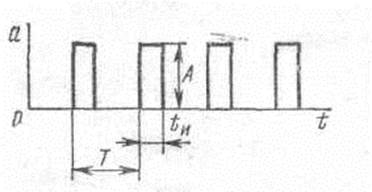
Рис.7. Периодические импульсы

Отношение периода Т к длительности t_и импульсов называют скважностью q=T/ t_и.

Скважность обычно колеблется в пределах от 2—10 (автоматика вычислительная техника) до 10 000 (радиолокация).

Приведенные на рис.5 импульсы идеализированы. Реальные импульсы искажены, что выражается обычно в замедлении нарастания и спада импульса, а также в спаде плоской вершины импульса (рис.8).

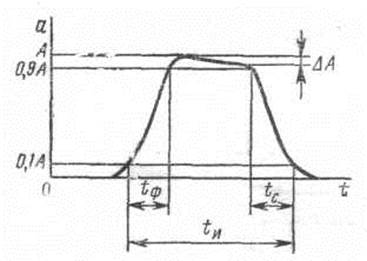
Рис.8. Параметры реальных импульсов

Реальные импульсы характеризуют следующими основными параметрами:

- амплитудой импульса А;

- длительностью импульса t_и, обычно определяемой на уровне 0,1А;

- длительностью фронта импульса t_ф — временем нарастания импульса от 0,1 А до 0,9 А;

- длительностью среза (спада) импульса t_с — временем спада импульса от 0,9 А до 0,1 А;

- неравномерностью (завалом) вер­шины импульса ΔА.

Цвета шума

Цвета шума — система терминов, приписывающая некоторым видам стационарных шумовых сигналов определённые цвета исходя из аналогии между спектром сигнала произвольной природы (точнее, его спектральной плотностью или, говоря математически, параметрами распределения случайного процесса) и спектрами различных цветов видимого света. Эта абстракция широко используется в отраслях техники, имеющих дело с шумом (акустика, электроника, физика и т. д.).

Цветовые соответствия различных типов шумового сигнала определяются с помощью графиков (гистограмм) спектральной плотности, то есть распределения мощности сигнала по частотам. Кроме того, при анализе реальных сигналов большое значение имеет оценка автокорреляционной функции процесса; из всех видов шума белый шум является единственным процессом, в котором значения сигнала в разные моменты времени не зависят друг от друга и никак не связаны (автокорреляция отсутствует). Для оценки порядка автокорреляции (является ли процесс интегрированным, чистым или дифференцированным белым шумом) используются различные статистические методы, например, тест Бройша — Годфри.

Белый шум

Белый шум — это сигнал с равномерной спектральной плотностью на всех частотах и дисперсией, равной бесконечности. Является стационарным случайным процессом.

Другими словами, такой сигнал имеет одинаковую мощность в одинаковой полосе частот любой части диапазона. К примеру, сигнал полосой в 20 Гц между 40 и 60 Гц имеет такую же мощность, что и сигнал полосой 20 Гц между 4000 и 4020 Гц. Неограниченный по частоте белый шум возможен только в теории, так как в этом случае его мощность бесконечна. На практике сигнал может быть белым шумом только в ограниченной полосе частот.

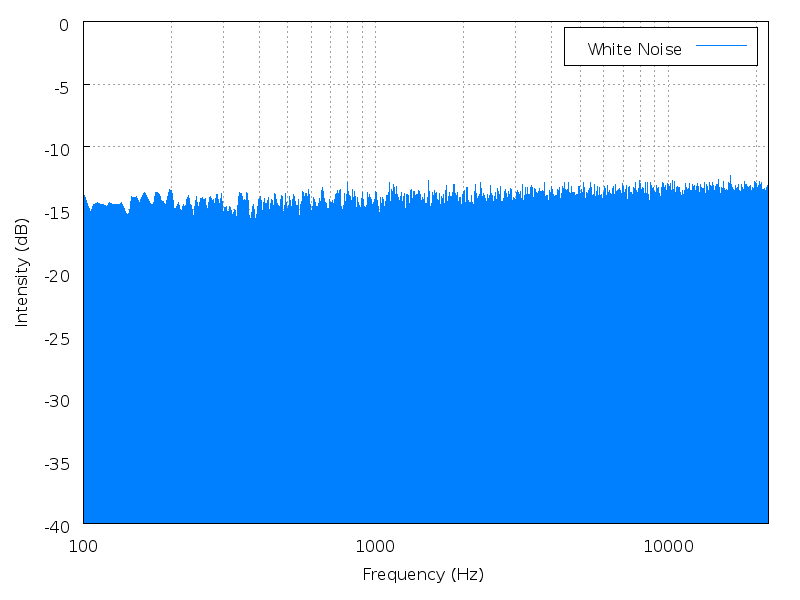
Рис.9. Спектр белого шума