Метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым.
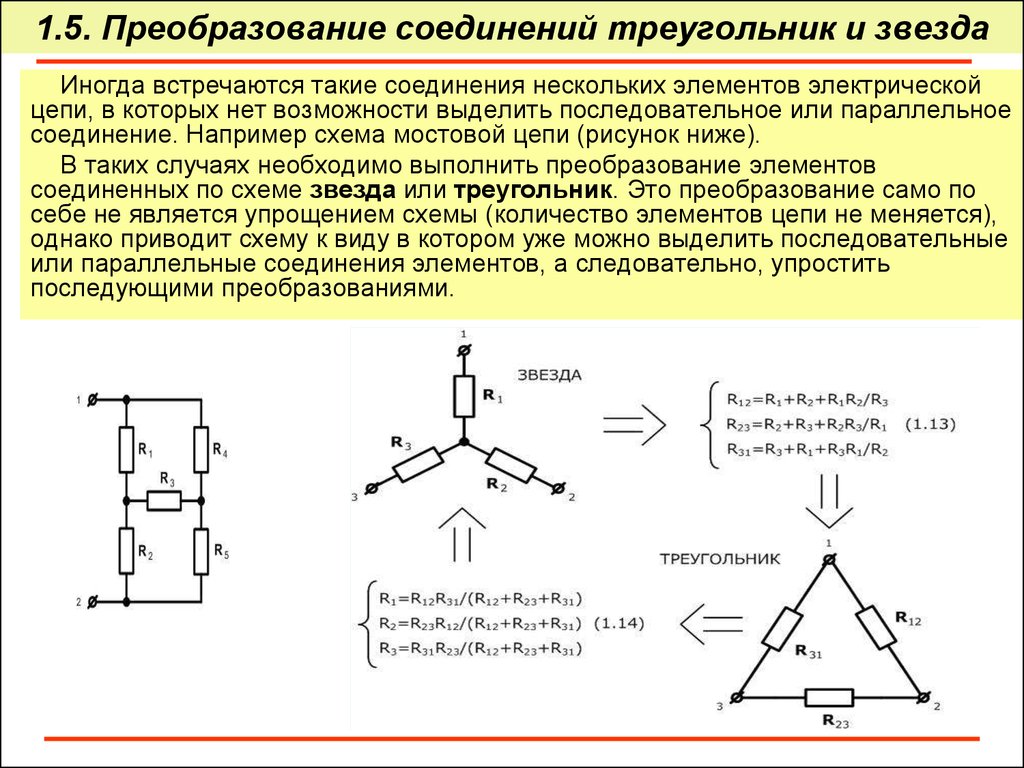
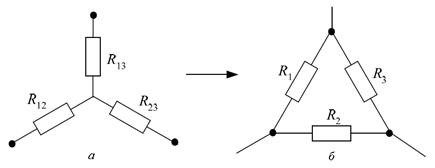

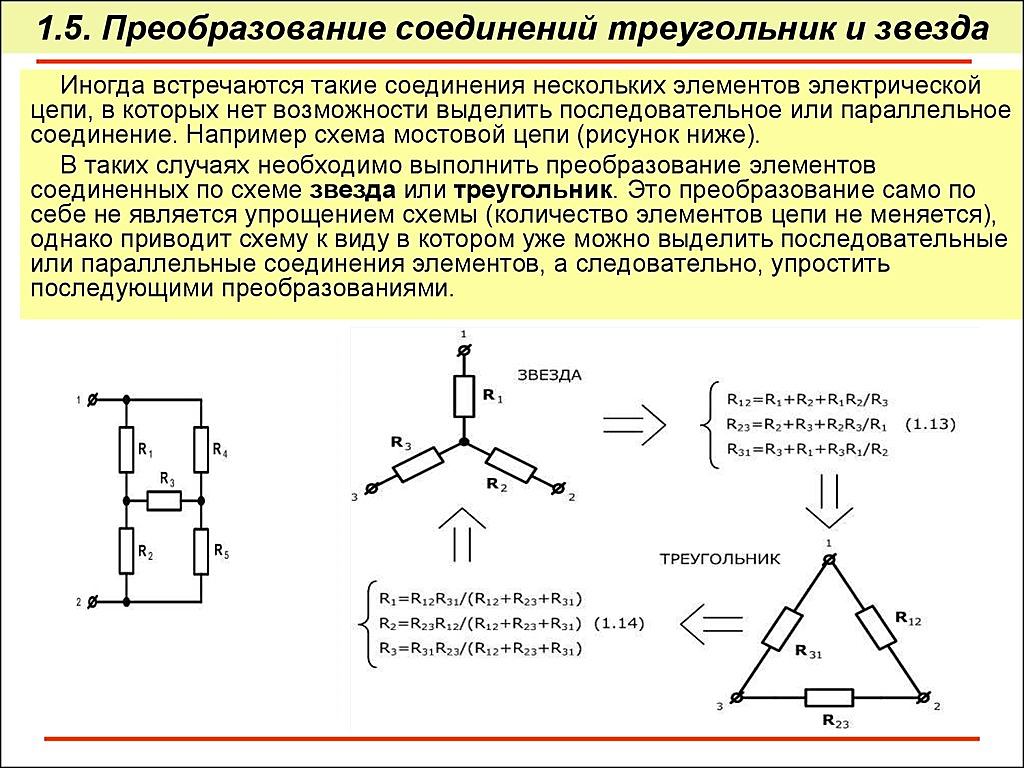
условием эквивалентности являются следующие уравнения:
а) при преобразовании треугольника в звезду:
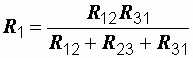 ;
; 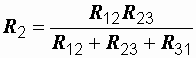 ;
; 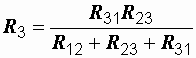
б) при преобразовании звезды в треугольник:
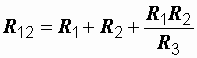 ;
; 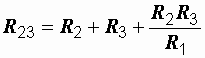 ;
; 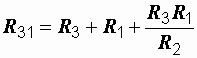 .
.
Методические указания к задаче 5
Однофазные цепи переменного тока
Последовательное соединение активно-реактивной нагрузки
Неразветвленная цепь переменного тока содержит активные и реактивные сопротивления, величины которых заданы в таблице вариантов.
Кроме того, известна одна из дополнительных величин.
Определить следующие
величины, если они не заданы в таблице вариантов:
1) полное сопротивление цепи –Z,
2) напряжение -U, приложенное к цепи.
3) силу тока в цепи - I;
4) угол сдвига фаз- ϕ
5) активную -Р, реактивную- Q и
полную -S мощности, потребляемые цепью.
Начертить в масштабе векторную диаграмму и пояснить ее построение.
После логических рассуждений пояснить, как изменится ток І* в цепи и угол
сдвига фаз, если частоту тока увеличить вдвое, а напряжение, приложенное к цепи, не
изменять
Пример: Электрическая цепь, питается от источника синусоидального тока с частотой 200 Гц и напряжением 120 В. Дано: R = 4 Ом, L = 6,37 мГн, C = 159 мкФ.
Вычислить ток в цепи, напряжения на всех участках, активную, реактивную, и полную мощности. Построить векторную диаграмму, треугольники сопротивлений и мощностей.
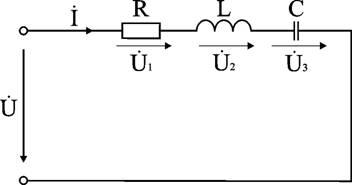
Анализ и решение задачи
1. Вычисление сопротивлений участков и всей цепи
Индуктивное реактивное сопротивление
XL = 2πf L = 2×3,14×200×6,37·10-3 Ом.
Емкостное реактивное сопротивление
XC = 1 / (2πf C) = 1 / (2×3,14×200×159·10-6) Ом.
Реактивное и полное сопротивления всей цепи:
X = XL - XC = 3 Ом; 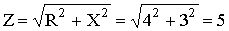 Ом.
Ом.
2. Вычисление тока и напряжений на участках цепи
Ток в цепи
I = U / Z = 120 / 5 А.
Напряжения на участках:
U1 = R I = 96 В; U2 = XL I = 192 В; U3 = XC I = 120 В.
3. Вычисление мощностей
Активная мощность
P = R I2 = U1 I = 2304 Вт.
Реактивные мощности:
QL = XL I2 = U2 I = 4608 ВАр; QC = XC I2 = U3 I = 2880 ВАр.
Полная мощность цепи
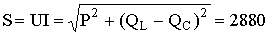 ВА.
ВА.
На комплексной плоскости в масштабе: в 1 см – 2 Ом, построим треугольник сопротивлений
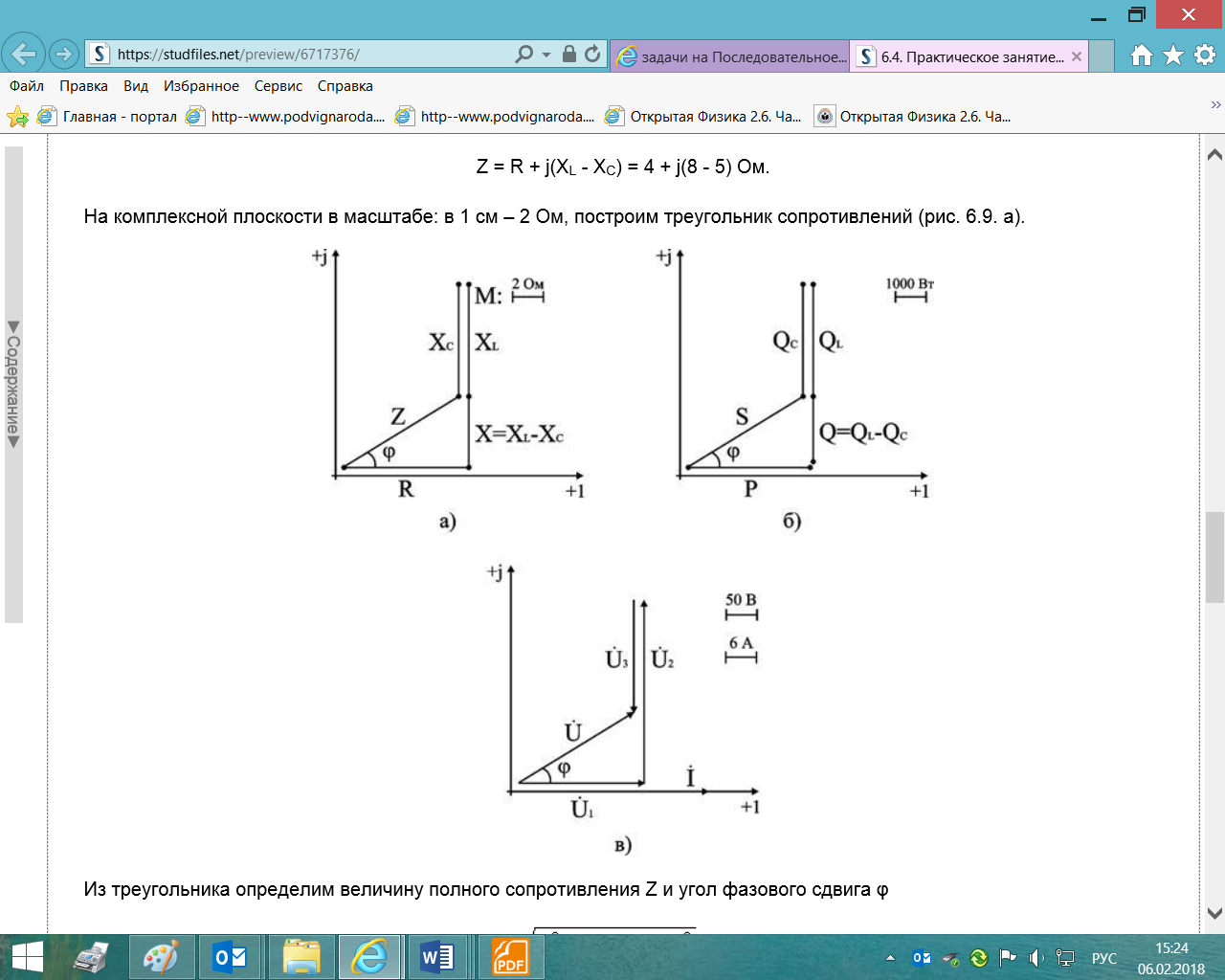
Из треугольника определим величину полного сопротивления Z и угол фазового сдвига φ
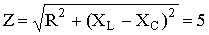 Ом;
Ом;
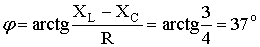 .
.
В данной цепи ток отстает по фазе от напряжения на угол φ. Зная величину тока I, определим мощности для отдельных элементов и всей цепи.
P = 2304 Вт; QL = 4608 ВАр; QC = 2880 ВАр.
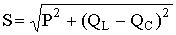 .
.
Треугольник мощностей в масштабе: в 1 см – 1000 Вт (ВАр); (ВА), построим (рис. 6.9. б) на основе выражения для полной мощности
S2 = P2 + (QL - QC)2.
Дата: 2018-12-28, просмотров: 577.