Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

6. ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ... 9

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ.. 10

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.. 11

9. РЯДЫ... 12

ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.. 13

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ.. 14

ТЕОРИЯ ВЕРОЯТНОСТЕЙ.. 14

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.. 16

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.. 17

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ.. 20

ДИСКРЕТНАЯ МАТЕМАТИКА.. 23

КРАТКОЕ СОДЕРЖАНИЕ (ПРОГРАММА) КУРСА.. 25

СПИСОК УЧЕБНОЙ ЛИТЕРАТУРЫ... 31

 

Формирование исходных данных к задачам

Каждая контрольная работа состоит из задач одного или нескольких разделов сборника.

Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.

Числовых данных параметров т и п определяются по двум последним цифрам своего шифра зачетки (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.

 

Таблица 1 (выбор параметра т)

А	0	1	2	3	4	5	6	7	8	9
т	1	2	3	4	5	1	2	3	4	5

 

Таблица 2 (выбор параметра п )

В	0	1	2	3	4	5	6	7	8	9
п	3	5	4	2	1	5	4	1	3	2

Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т =4, п =1. Полученные т = 4 и п = 1 подставляются в условия всех задач контрольной работы этого студента.

 

Линейная алгебра

Действия с матрицами.

Выполнить действия:

а) 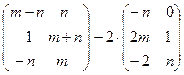;             б) .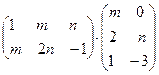

Вычисление определителей.

Вычислить определитель  двумя способами:

а) по правилу «треугольников»; б) разложением по строке.

Обратная матрица.

Найти обратную матрицу к матрице 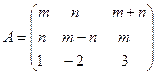 и проверить выполнение равенства .

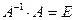Системы линейных уравнений.

Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) с помощью вычисления обратной матрицы, записав систему в матричном виде :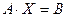

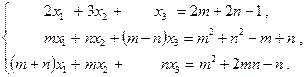
Собственные числа и собственные векторы.

Найти собственные числа и соответствующие им собственные векторы для матрицы .

 

 

Аналитическая геометрия

Прямая на плоскости.

Построить треугольник, вершины которого находятся в точках 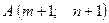, , 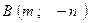 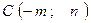и найти:

1) координаты точки пересечения медиан;

2) длину и уравнение высоты, опущенной из вершины А;

3) площадь треугольника;

4) систему неравенств, задающих внутренность треугольника АВС.

Кривые второго порядка на плоскости.

Составить уравнение кривой, для каждой точки которой отношение расстояния до точки  к расстоянию до прямой  равно . Привести уравнение к каноническому виду и определить тип кривой.