| № п./п. | Диаметр зёрен, мм | Коэффициент пористости, % | Коэффициент проницаемости, мД |
| 1 | 0,503–0,381 | 40 | 344,81 |
| 2 | 0,381–0,280 | 40 | 65,89 |
| 3 | 0,280–0,221 | 40 | 43,46 |
| 4 | 0,221–0,191 | 40 | 40,91 |
| 5 | 0,191–0,175 | 40 | 26,36 |
| 6 | 0,175–0,134 | 40 | 10,19 |
| 7 | 0,134–0,114 | 40 | 9,93 |
| 8 | 0,114–0,105 | 40 | 9,26 |
Оценить качественную зависимость изменения проницаемости от размера пор в предположении, что фильтрация флюидов происходит через капиллярные поры, а пористая среда рассматривается как идеальная система, можно из соотношений законов Пуазейля и Дарси.
Уравнение Пуазейля описывает объёмную скорость течения жидкости через пористую среду, которая представляется в виде системы прямых трубок одинакового сечения длиной (L), равной длине пористой среды:
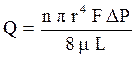, (1.26)
где n – число пор на единицу площади фильтрации;
r – радиус порового канала;
F – площадь фильтрации;
DР – перепад давления;
L – длина порового канала;
m – вязкость жидкости.
По определению (1.4) коэффициент пористости среды, через которую проходит фильтрация, можно представить следующим образом:
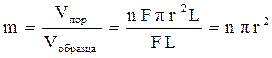. (1.27)
С учётом (1.27), уравнение Пуазейля (1.26) преобразуется в выражение:
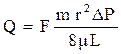. (1.28)
Сравнивая полученное нами уравнение (1.28) с уравнением Дарси (Q = k·F·∆P/μ·L) и приравняв правые части этих уравнений, сократив подобные параметры, получим выражение для искомой взаимосвязи проницаемости, пористости и радиуса порового канала:
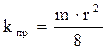. (1.29)
Анализируя полученное выражение (1.29) видно, что взаимосвязь между проницаемостью и пористостью нелинейная. Для графической линеаризации зависимости (у = а + bх) её представляют в полулогарифмических координатах → "lg (kпр) ↔ m".
Оценочные измерения показали, что радиусы пор, по которым происходит движение жидкостей, находятся в пределах от 5 до 30 мкм. Полученная корреляционная взаимосвязь (1.29) используется при проведении прогнозных и модельных расчётов коэффициентов проницаемости для образцов кернового материала с известной пористостью.
Выражение (1.29) используется и для оценки радиуса (размера) порового канала для образцов кернового материала с известными величинами пористости и проницаемости:
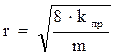. (1.30)
Если выразить проницаемость в мкм2, то и радиус поровых каналов в мкм будет рассчитываться по эмпирическому выражению:
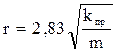. (1.31)
Уравнения (1.29–1.31) справедливы только для однородной пористой среды, например для кварцевого песка, и характеризуют взаимосвязь между пористостью, проницаемостью, радиусом порового канала. Для реальных коллекторов оценка радиуса порового канала производится с учётом структурных особенностей порового пространства пород. Обобщённым выражением для этих целей является, например, эмпирическое уравнение Ф. И. Котяхова:
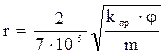, (1.32)
где r – радиус пор;
j – структурный коэффициент, учитывающий извилистость порового пространства.
Величины j оценивают экспериментально на модельных средах путём измерения электрического сопротивления пород. Как правило, значения коэффициентов j обратно пропорциональны величинам коэффициентов пористости (m). По экспериментальным данным для керамических, пористых сред при изменении пористости от 0,39 до 0,28, коэффициент j изменяется от 1,7 до 2,6.
Для приближённой оценки структурного коэффициента зернистых пород в литературе предложены различные эмпирические выражения, одно из которых представлено ниже:
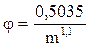. (1.33)
При проведении инженерных расчётов для известных типов коллекторов часто используют эмпирические зависимости, полученные теоретическим путём. Допустим, фильтрация идёт через поры круглого сечения и радиус порового канала известен. Тогда оценку коэффициента проницаемости при фильтрации жидкости через поры круглого сечения рассчитывают, используя взаимосвязь коэффициента проницаемости от радиуса порового канала, полученную из сопоставления уравнений Пуазейля и Дарси:
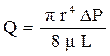и 
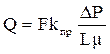. (1.34)
Причём, пористая среда представляет собой систему трубок. Общая площадь пор, через которые идет фильтрация флюидов, оценивается как F = π·r2. Отсюда, величину π можно выразить как π = F/r2.
Подставив эту величину в уравнение Пуазейля (1.34, левое выражение) и сократив одинаковые параметры в выражениях (1.34, левом и правом), получим корреляционную связь между коэффициентом проницаемости породы от радиуса порового канала:
kпр = r2/8. (1.35)
Если радиус r измеряется в см, а коэффициент проницаемости в Д (1Д ≈ 1,02·10–8 см2 или = 1,01327·10–8), то вводится соответствующий коэффициент пересчёта, равный 9,869·10–9. Тогда коэффициент проницаемости при фильтрации жидкости через капилляр или канал оценивается эмпирическим выражением:
k пр = r2/(8·9,869·10–9) = 12,5·106 × r 2. (1.36)
Для трещинного типа коллектора оценка коэффициента проницаемости при фильтрации жидкости только через поры-трещины осуществляется с использованием взаимосвязи коэффициента проницаемости от высоты поровой трещины, полученной из соотношений уравнений Дарси и Буссинеска.
По уравнению Буссинеска, потеря давления при течении жидкости через щель очень малой высоты описывается соотношением:
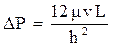, (1.37)
где v – линейная скорость фильтрации жидкости;
h – высота трещины.
Выделив из уравнения Дарси величину перепада давления
∆P = v·μ·L/kпр и приравняв правые части рассматриваемых уравнений, после сокращения одинаковых параметров получим выражение для оценки коэффициента проницаемости:
kпр = h2/12. (1.38)
С учетом того, что h измеряется в см, а коэффициент проницаемости в Д, вводится соответствующий коэффициент пересчёта, равный 9,869·10–9. Тогда коэффициент проницаемости пористой среды при фильтрации жидкости в ней через трещину оценивается:
k пр = h2/(12·9,869·10–9) = 84,4·105·h2. (1.39)
Уравнения (1.36 и 1.39) используются для теоретической оценки коэффициентов проницаемости для конкретного вида пор.
Рассмотрим пример. Через кубик породы размером 10·10·10 см3 проницаемостью в 10 мД фильтруется жидкость при линейной режиме течения вязкостью 1 сПз, при градиенте давления (∆Р/∆L) = 25 кПа/м (0,25 кПа/см). Определить дебит фильтрующейся жидкости?
Решение. Рассмотренный случай описывает капиллярный вид фильтрации. То есть, фильтрация равномерная и проходит через всю площадь образца, имеющего капиллярную пористость. Дебит (Q1) составит
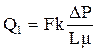= 100·0,01·(0,25/1) = 0,25 см3/с.
Если в этом кубике будет один канал диаметром 0,2 мм той же длины, что и кубик, то при том же градиенте давления дебит фильтрующейся жидкости через этот канал будет:
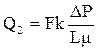= 12,5·106·(0,02/2)2·π·(0,02/2)2·0,25 = 0,1 см3/с.
Следовательно, при наличии в кубике одного канала и капиллярной пористости, то есть при наличии неравномерной фильтрации, суммарный дебит (Q3) фильтрующейся жидкости составит
Q3 = Q2 + Q1 = 0,1 + 0,25 = 0,35 (см3/с).
Суммарный дебит (Q3) имеет величину на 40 % больше, чем при капиллярной фильтрации (Q1).
Если в кубике вместо канала имеется трещина высотой 0,2 мм и шириной 10 см, её влияние на общий дебит жидкости, фильтрующейся через породу, будет существенным:
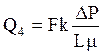= (84,4·105·(0,02)2·0,02·10·0,25)/1 = 168,8 см3/с.
Суммарный дебит (Q5) с учётом и капиллярной фильтрации (Q1) составит
Q5 = Q4 + Q1 = 168,8 + 0,25 = 169,05 (см3/с).
По сравнению с первым случаем (Q1) суммарный дебит увеличился в 675 раз.
Пример свидетельствует о большом влиянии наличия каналов и особенно трещин в породе на объём фильтрующейся жидкости. В коллекторах смешанного типа (уравнение 1.7) наличие трещин существенно увеличивает проницаемость продуктивных пластов:
mтрещ<< mгран → kпр/трещ >> kпр/гран. (1.40)
На практике проницаемость породы определяют в лабораторных условиях по керновому материалу.
Виды проницаемости
При разработке нефтяных и газовых месторождений встречаются различные виды фильтрационных потоков: движение нефти или газа, совместное движение двух или трёхфазного потока. В пористой среде одновременно движутся нефть, газ и вода или их смеси. В связи с этим проницаемость одной и той же пористой среды для одной фазы (жидкости или газа) будет изменяться в зависимости от соотношения компонентов в смеси. Поэтому для характеристики проницаемости нефтесодержащих пород введены понятия абсолютной, фазовой (эффективной) и относительной фазовой проницаемостей.
Проницаемость абсолютная (физическая) характеризует проницаемость пористой среды для газа или однородной жидкости при выполнении следующих условий:
· отсутствие физико-химического взаимодействия между пористой средой и этим газом или жидкостью, фаза химически инертна по отношению к породе;
· полное заполнение всех пор среды этим газом или жидкостью.
Абсолютная проницаемость характеризует фильтрационную способность горной породы для инертного в физико-химическом отношении флюида. Для реальных продуктивных нефтяных пластов эти условия не выполняются.
Проницаемость фазовая (эффективная) – это проницаемость пористой среды для данного газа или жидкости при одновременной фильтрации многофазных систем. То есть при наличии в порах другой фазы (жидкости или газа) или других фаз (газ–нефть, нефть–вода, вода–газ, газ–нефть–вода) независимо от того, находятся они в статическом состоянии (например, капиллярно связанная вода) или принимают участие в совместной фильтрации. Величины фазовых проницаемостей зависят не только от физических свойств пород, но и от степени насыщенности порового пространства жидкостями или газом и от их физико-химических свойств. При фильтрации смесей коэффициент фазовой проницаемости намного меньше коэффициента абсолютной проницаемости и неодинаков для пласта в целом.
Относительная фазовая проницаемость определяется отношением величины фазовой проницаемости к величине абсолютной для той же породы. Относительные проницаемости (k', % или в дол. ед.) породы для нефти и воды (газа аналогично) оцениваются как:
k'н = (kн/k)·100, %; k'в = (kв/k)·100, %; (1.41)
где kн и kв – фазовые проницаемости для нефти и воды;
k – абсолютная проницаемость породы.
Фазовая и относительная фазовая проницаемости горных пород зависят от степени насыщения (насыщенности) породы флюидами, градиента давления, соотношения фаз, физико-химических свойств породы и флюидов и определяются экспериментально.
Насыщенность коллекторов
Насыщенность – один из важных параметров продуктивных пластов, характеризует запасы нефти (газа и воды) в пласте, количественно оценивается величиной коэффициента S, тесно связан с фазовыми проницаемостями флюидов:
· водонасыщенностью – Sв;
· газонасыщенностью – Sг;
· нефтенасыщенностью – Sн.
Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены все поры: капилляры, каналы, трещины. При миграции и аккумуляции углеводороды, вследствие меньшей плотности, стремились к верхней части ловушек, выдавливая вниз воду, и та легче всего уходила из трещин, каналов, а оставалась в микропорах.
Из капиллярных, особенно субкапиллярных пор и микротрещин вода плохо вытесняется, в силу действия капиллярных явлений. В порах маленького размера вода прочно удерживается молекулярно-повер-хностными и капиллярными силами. Поэтому в пласте всегда находится остаточная, погребённая вода (Sв ост) с периода формирования залежи.
Количество остаточной воды (Sв ост) связано с генетическими особенностями формирования залежей нефти и газа. Её величина зависит от содержания цемента в коллекторах, в частности, от содержания в них глинистых минералов: каолинита, монтмориллонита, гидрослюд.
Обычно для сформированных нефтяных месторождений остаточная водонасыщенность изменяется в диапазоне от 6 до 35 %. Соответственно, нефтенасыщенность (Sн), равная 65 % и выше (до 90 %), в зависимости от "созревания" пласта считается хорошим показателем залежи.
Подобная закономерность наблюдается далеко не для всех регионов. Например, в Западной Сибири встречается много, так называемых, недонасыщенных нефтью пластов. В залежах иногда наблюдаются переходные зоны (ПЗ), в которых содержится рыхлосвязанная вода. Толщины ПЗ могут достигать десятков метров.
При создании депрессий на забоях добывающих скважин вода из этих зон попадает в фильтрационные потоки и увеличивает обводнённость продукции, что осложняет выработку запасов нефти.
Такие явления характерны для месторождений: Суторминского, Советско-Соснинского, Талинского, Средневасюганского и других. Очень часто это проявляется для малых малодебитных месторождений Западной Сибири.
В пределах нефтяных залежей большая начальная нефтенасыщенность отмечается в купольной части структур. К зоне водонефтяного контакта (ВНК) её величина может значительно снижаться.
Количество углеводородов, содержащихся в продуктивном пласте, зависит от насыщенности порового пространства породы нефтью, газом и водой. Остаточная водонасыщенность, обусловленная капиллярными силами, не влияет на основную фильтрацию нефти и газа.
Водонасыщенность (Sв) характеризует отношение объёма открытых пор, заполненных водой, к общему объёму пор горной породы. Аналогичны определение для нефте- (Sн) и газонасыщенности (Sг):
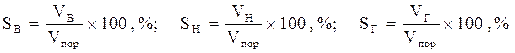, (1.42)
где Vв, Vн, Vг – соответственно объёмы воды, нефти и газа в поровом объёме (Vпор) породы.
Параметр насыщенности нормирован и равен единице (S=1) или 100 %. То есть, для образцов пород, в случае фильтрации систем: нефти, газа и воды справедливо соотношение:
Sв + Sн + Sг = 1, Sг = 1 – (Sв + Sн). (1.43)
От объёма остаточной воды в залежи зависит величина статической полезной ёмкости коллектора. Статическая полезная ёмкость коллектора (Пст) характеризует объём пор и пустот, которые могут быть заняты нефтью или газом. Эта величина оценивается как разность объёма сообщающихся пор и объёма, занятого остаточной водой:
Пст = Vсообщ. пор – Vв ост . (1.44)
В зависимости от перепадов давлений, существующих в пористых средах, свойств фильтрующихся жидкостей, свойств поверхности пород, соприкасающихся с пластовыми флюидами, та или иная часть жидкости (неподвижные пленки у поверхности породы, капиллярно удерживаемая жидкость в порах) не движется в порах.
Величина порового пространства, занятая остаточной водой влияет на динамическую полезную ёмкость коллектора. Динамическая полезная ёмкость коллектора (Пдин) характеризует относительный объём пор и пустот, через которые может происходить фильтрация нефти или газа в условиях, существующих в пласте.
На практике насыщенность пород определяют в лабораторных условиях по керновому материалу в аппаратах Закса или по данным геофизических исследований в открытых стволах скважин.
Дата: 2018-12-21, просмотров: 243.
