Изучение математики в старшей школе даёт возможность достижения обучающимися следующих результатов.

Личностные:

1) сформированность мировоззрения, соответствующего современному уровню развития науки; критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

2) готовность и способность вести диалог с другими людьми, достигать в нём взаимопонимания, находить общие цели и сотрудничать для их достижения;

3) навыки сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;

4) готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

5) эстетическое отношение к миру, включая эстетику быта, научного и технического творчества;

6) осознанный выбор будущей профессии и возможностей реализации собственных жизненных планов; отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем.

Метапредметные:

1) умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

2) умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

3) владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

4) готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

5) умение использовать средства информационных и коммуникационных технологий (далее — ИКТ) в решении когнитивных, коммуникативных и организационных задач с соблюдением требований эргономики, техники безопасности, гигиены, ресурсосбережения, правовых и этических норм, норм информационной безопасности;

6) владение языковыми средствами — умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

7) владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.

Предметные:

1) сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

2) сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

3) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;

4) владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений

и неравенств;

5) сформированность представлений об основных понятиях, идеях и методах математического анализа;

6) сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; сформированность умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

7) владение навыками использования готовых компьютерных программ при решении задач.

Содержание учебного предмета «Математика» (базовый уровень)

Класс

Алгебра и начала математического анализа.

Повторение

Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений. Модуль числа и его свойства. Решение задач на движение и совместную работу с помощью линейных и квадратных уравнений и их систем. Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков. Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции 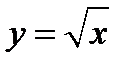. Графическое решение уравнений и неравенств.

Действительные числа

Понятие натурального числа. Множества чисел. Свойства действительных чисел. Метод математической индукции. Перестановки. Размещение. Сочетание.

Рациональные уравнения и неравенства.

Рациональные выражения. Формула бинома Ньютона, суммы и разности степеней. Рациональные уравнения. Системы рациональных уравнений. Метод интервалов решения неравенств. Рациональные неравенства. Нестрогие неравенства. Системы рациональных неравенств.

Корень степени n.

Понятие функции и ее графика. Функция у=х^n. Понятие корня степени n. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени n.

Степень положительного числа.

Степень с действительным показателем, свойства степени. Степенная функция и ее свойства и график. Иррациональные уравнения.

Метод интервалов для решения неравенств.

Преобразования графиков функций: сдвиг вдоль координатных осей, растяжение и сжатие, отражение относительно координатных осей. Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля.

Логарифмы.

Логарифм числа, свойства логарифма. Десятичный логарифм. Число е. Натуральный логарифм. Преобразование логарифмических выражений.

 Показательные и логарифмические уравнения и неравенства.

Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график.

Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических неравенств.

Взаимно обратные функции. Графики взаимно обратных функций.

Уравнения, системы уравнений с параметром.

Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график.

Синус и косинус угла.

Тригонометрическая окружность, радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. Основное тригонометрическое тождество и следствия из него. Значения тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°, 180°, 270°. ( 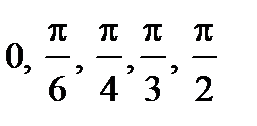 рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента..

Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции. Четность и нечетность функций. Сложные функции.

Тригонометрические функции 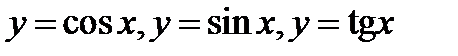. Функция 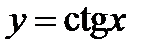. Свойства и графики тригонометрических функций.

Арккосинус, арксинус, арктангенс числа. Арккотангенс числа. Простейшие тригонометрические уравнения. Обратные тригонометрические функции, их свойства и графики. Решение простейших тригонометрических неравенств.

Тригонометрические уравнения и неравенства.

Решение тригонометрических уравнений.

Вероятность и статистика.

Решение задач на табличное и графическое представление данных. Использование свойств и характеристик числовых наборов: средних, наибольшего и наименьшего значения, размаха, дисперсии. Решение задач на определение частоты и вероятности событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами. Решение задач с применением комбинаторики. Решение задач на вычисление вероятностей независимых событий, применение формулы сложения вероятностей. Решение задач с применением диаграмм Эйлера, дерева вероятностей, формулы Бернулли.

Условная вероятность. Правило умножения вероятностей. Формула полной вероятности.

Дискретные случайные величины и распределения. Независимые случайные величины. Распределение суммы и произведения независимых случайных величин.

Математическое ожидание и дисперсия случайной величины. Математическое ожидание и дисперсия суммы случайных величин. Геометрическое распределение. Биномиальное распределение и его свойства.

Непрерывные случайные величины. Понятие о плотности вероятности. Равномерное распределение.

Показательное распределение, его параметры.

Понятие о нормальном распределении. Параметры нормального распределения. Примеры случайных величин, подчиненных нормальному закону (погрешность измерений, рост человека).

Неравенство Чебышева. Теорема Бернулли. Закон больших чисел. Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе.

Ковариация двух случайных величин. Понятие о коэффициенте корреляции. Совместные наблюдения двух случайных величин. Выборочный коэффициент корреляции.

Геометрия.

Повторение .

Решение задач с применением свойств фигур на плоскости. Задачи на доказательство и построение контрпримеров. Использование в задачах простейших логических правил. Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками. Решение задач с использованием фактов, связанных с окружностями. Решение задач на измерения на плоскости, вычисление длин и площадей. Решение задач с помощью векторов и координат.

Введение

Наглядная стереометрия. Фигуры и их изображения (куб, пирамида, призма). Основные понятия стереометрии и их свойства. Сечения куба и тетраэдра.

Параллельность прямых и плоскостей

Точка, прямая и плоскость в пространстве, аксиомы стереометрии и следствия из них. Взаимное расположение прямых и плоскостей в пространстве. Параллельность прямых и плоскостей в пространстве. Изображение простейших пространственных фигур на плоскости.

Расстояния между фигурами в пространстве.

Перпендикулярность прямых и плоскостей

Углы в пространстве. Перпендикулярность прямых и плоскостей.

Проекция фигуры на плоскость. Признаки перпендикулярности прямых и плоскостей в пространстве. Теорема о трех перпендикулярах.

Многогранники

Многогранники. Параллелепипед. Свойства прямоугольного параллелепипеда. Теорема Пифагора в пространстве. Призма и пирамида. Правильная пирамида и правильная призма. Прямая пирамида. Элементы призмы и пирамиды.

Класс