| Классы группировки | Точные границы классов | Частоты данных (¦) | Накопленные частоты (¦cum) | Процентная сумма накопленных частот (%) |
| 10 9 8 7 6 5 4 3 2 1 | 54,5-59,5 49,5-54,5 44,5-49,5 39,5-44,5 34,5-39,5 29,5-34,5 24,5-29,5 19,5-24,5 14,5-19,5 9,5-14,5 | 1 1 3 4 6 7 12 6 8 2 | 50 49 48 45 41 35 28 16 10 2 | 1,00´100=100 0,98´100=98 0,96´100=96 0,90´100=90 0,82´100=82 0,70´100=70 0,56´100=56 0,32´100=32 0,20´100=20 0,04´100=4 |
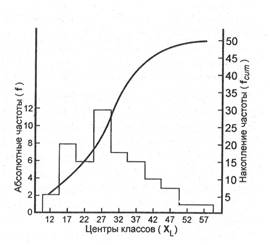
Рис. 1.1.6. Гистограмма и кривая накопленных частот первичных результатов
исследования выборки (см. табл. 1.1.5).
На основе описанного только что метода представления первичных результатов - табличного и графического - может быть произведен расчет статистических показателей. Цель этих расчетов в том, чтобы с помощью простых показателей дать математическую оценку результатов эксперимента или наблюдения. Наиболее часто используемыми статистическими показателями распределения являются меры центральной тенденции и меры рассеивания.
Меры центральной тенденции. Среди множества мер центральной тенденции для обработки результатов психологических исследований чаще всего используют среднюю арифметическую величину (М) и медиану (Me).
В случае небольшого числа первичных результатов и отсутствия предварительной их группировки значение средней арифметической получают путем последовательного суммирования исходных величин (X) с последующим делением этой суммы на общее количество исходных данных (N):
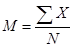 .
.
Если массив первичных данных был подвергнут предварительной группировке, то для вычисления средней арифметической величины проделывают следующие операции. Для каждого класса группировки определяют произведение частоты класса (f) на центр группировки класса (X), а затем суммируют эти произведения и полученную величину делят на общее количество исходных данных N:
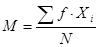 .
.
Так, для примера, приведенного в табл. 1.1.4, мы имеем: 57+52+141+ +168+222+224+324+132+136+24 =1480 и 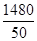 = 29,60, т. е. М = 29,60.
= 29,60, т. е. М = 29,60.
Второй мерой центральной тенденции, особенно для порядковых величин, является медиана. Медиана - это точка на измерительной шкале, выше которой находится точно половина наблюдений и ниже которой - также точно половина наблюдений. В этом определении важно подчеркнуть, что медиана - это точка на шкале, а не отдельное измерение или наблюдение. На примере данных табл. 1.1.4 продемонстрируем этапы вычисления медианы на основе сгруппированных данных.
1. Находим половину наблюдений в массиве данных т. е. N/2. В нашем примере: 50:2 = 25,0.
2. Суммируем частоты, начиная с минимального класса группировки, до класса, содержащего половину необходимых наблюдений т. е. медиану. Для нашего примера, в котором N =50, половиной наблюдений будет 25. Итак, по данным табл. 1.1.4 это: 2 + 8 + 6 + 12 = 28. Отсюда очевидно, что медиана предположительно расположена в 4-м классе группировки, точные границы которого 24,5 и 29,5.
3. Определяем, сколько же наблюдений из класса, содержащего медиану, необходимо для того, чтобы найти ее. Поскольку сумма накопленных частот из предыдущих трех классов равна 16 (см. табл. 1.1.5), то ясно, что из медианного класса необходимо еще 9 наблюдений, а именно 25-16 =9.
4. Вычисляем ту долю интервала на шкале, которая позволит определить точное положение медианы. Если в медианном классе имеем 12 наблюдений и наблюдения в пределах класса распределены равномерно, то при ширине класса, равной 5 единицам, получаем: 9/12´5 = 3,75.
5. Прибавляем полученный результат к нижней точной границе класса группировки, содержащего медиану: 24,5+3,75 = 28,25. Это и есть ее значение: Mе = 28,25.
Существует аналитическая формула для интерполяции медианы:
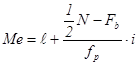 ,
,
где l - нижняя точная граница класса группировки содержащего медиану; Fb - сумма частот классов* ниже l; fp - сумма частот класса, содержащего медиану; N - число наблюдении или измерений; i - ширина класса группировки.
* Величина F b в данной формуле соответствует по своему смыслу величине накопленных частот (fcum), расчет которой был продемонстрирован выше.
Как видно из нашего примера, когда распределение первичных результатов наблюдений или измерений отличается от нормального, то величины средней арифметической и медианы не совпадают: 29,60¹28,25.
Меры изменчивости. В качестве мер изменчивости результатов, характеризующих степень рассеивания отдельных величин вокруг средней арифметической, используются разные меры в зависимости от примененных шкал измерения. Для характеристики рассеивания величин интервальных шкал и шкал отношений пользуются значением среднеквадратичного отклонения (s). Для величин порядковых шкал используют значения полуквартильных отклонений (Q1, и Q3).
При несгруппированных данных произведем расчет так называемого стандартного отклонения, обозначаемого S. Понятие стандартного отклонения (S) на практике чаще всего используется как синоним среднего квадратичного отклонения (s). Расчет делается следующим образом:
1. Рассчитаем среднюю арифметическую величину (М).
2. Находим отклонение (х) каждого результата измерения (X) от средней арифметической величины: х=Х-М.
3. Возводим найденное значение отклонения каждого результата от среднего в квадрат: x2.
4. Суммируем значения квадратов отклонений всех результатов: åx2.
5. Делим сумму квадратов отклонений на общее число наблюдений (N) и получаем величину, называемую дисперсией (D):
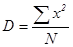
6. Извлекаем корень квадратный из дисперсии и получаем величину, называемую стандартным отклонением (S), или среднеквадратичное отклонение (s):
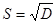 , s =
, s = 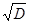 .
.
Таблица 1.1.6
Расчет дисперсии ( D) и стандартного отклонения (S) (при N=10)
| Х | х | х2 |
| 13 17 15 11 13 11 17 13 11 11 | 0,2 -3,8 -1,8 2,2 0,2 2,2 -3,8 0,2 2,2 2,2 | 0,04 14,44 3,24 4,84 0,04 4,84 14,44 0.04 4,84 4,84 |
å х2 = 51,60
Таким образом: D 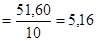 и S
и S 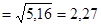 .
.
Приведем все описанные расчеты для конкретного примера и определим дисперсию и стандартное отклонение для выборки, состоящей из результатов 10 измерений: 13; 17; 15; 11; 13; 11; 17; 13; 11; 11. Для начала рассчитаем среднюю арифметическую величину: она оказывается равна 13,2. Для облегчения дальнейших расчетов составляем табл. 1.1.6. В 1 -и графе таблицы записываем первичные данные (X), во 2-й - отклонения их значений от средней арифметической (х) и в 3-й - квадраты отклонений (х2).
При сгруппированных данных формула расчета дисперсии приобретает следующий вид:
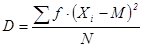 ,
,
где f - частота каждого из классов группировки; Xi - центр каждого из классов группировки; М - средняя арифметическая величина, а N - число измерений.
Различают два полуквартильных отклонения - для левой и правой сторон распределения экспериментальных данных. Каждое из полуквартильных отклонений представляет собой величину, соответствующую половине области распределения центральных 50% данных на шкале измерений. Очевидно, что любое распределение экспериментальных данных может быть разделено на четыре равные части, каждая из которых охватывает 25% наблюдений. Если отсчитывать наблюдения, начиная от минимальной величины на измерительной шкале, то точка Q1 , отделяющая первые 25% наблюдений от остальных, определит границу первого квартиля. Та же самая процедура счета, производимая от максимальной величины, отделяет последний, т. е. четвертый, квартиль; сама же точка на шкале обозначается как Q3 . Наконец медиана, согласно ее определению, позволяет идентифицировать второй и третий квартили: точка их разделения на шкале и соответствует медиане. Она получила обозначение Q2. Половина же интервала на измерительной шкале, заключенного между точками Q1 и Q3 и есть полуквартильные отклонения. Только в случае нормального, т. е. симметричного, распределения данных точка Q2 совпадает с местоположением медианы. Следовательно, с помощью полуквартильных отклонений можно определять рассеивание экспериментальных данных вокруг медианы.
Обратимся снова к табл. 1.1.4 и расчету мер центральной тенденции. Ранее для приведенных там данных мы рассчитали, что Me = 28,25, и таким образом определили точку Q2. Теперь нам предстоит найти точки Q1 и Q3. В случае нормального, т. е. строго симметричного, распределения данных точки Q1и Q3 можно рассматривать в качестве медиан: Q1 - для левого интервала (от начала шкалы измерений до точки Q2), a Q3 - для правого интервала (от конца шкалы до той же точки Q2). Поэтому дальнейшие процедуры расчетов значений Q1 и Q3 будут аналогичны той, которую мы рассматривали при вычислении медианы. То есть мы имели право воспользоваться приведенной выше аналитической формулой для интерполяции медианы, а именно
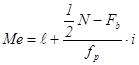 .
.
1. Прежде всего укажем, что значение i - ширины класса группировки - нам известно, из задания: i = 5 (как для левого интервала, так и для правого).
2. Что касается N - числа измерений, то согласно определению медианы вообще, а в нашем случае точки Q3 в частности, оно должно быть одинаковым в обоих рассматриваемых интервалах: Nл = Nпр = 25 при общем числе измерений, равном 50. Отсюда

3. Анализируя группировку данных, приведенную в табл. 1.1.4, нетрудно заметить, что классом группировки, предположительно содержащим половину наблюдений левого интервала, является 3-й класс, а таким же классом для правого интервала - 6-й класс. Исходя из этого, по табл. 1.1.4 легко определить, что
для левого интервала l =19,5; Fb=10; fp= 6;
для правого интервала l =39,5; Fb = 9; fp = 6.
4. Пользуясь найденными значениями величин, производим необходимые расчеты медиан обоих интервалов:
для левого Q1=19,5 + 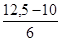 ×5 = 21,58,
×5 = 21,58,
для правого Q3 = 39,5- 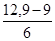 ×5 = 36,58.
×5 = 36,58.
5. Согласно определению квартального отклонения следует, что
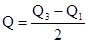 ,
,
т. е. в нашем примере Q = 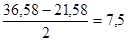 .
.
6. Однако этот результат получен нами для нормального распределения данных. На самом же деле, как показывает табл. 1.1.4, в нашем примере мы имеем дело с явно асимметричным распределением. Поэтому истинные полуквартильные отклонения в данном случае необходимо было рассчитывать с учетом вычисленного значения для медианы (или Q2), a именно, что Mе = 28,25. Тогда мы получаем
для левого интервала Q2 – Q1 = 28,25-21,58 = 6,67,
для правого интервала Q3 - Q2 = 36,58-28,25 = 8,33.
С помощью данного приема можно очень легко определить право- и левостороннюю асимметрию любого распределения:
если Q3 - Q1 > Q2 - Q1 то имела место правосторонняя асимметрия;
если Q3 - Q2 < Q2 - Q1, то - левосторонняя.
И только при равенстве указанных разностей можно говорить о строго симметричном распределении.
Для каких целей служат меры центральной тенденции (М или Me) и меры изменчивости (D, S, s, Q)? Во-первых, эти меры используются для интерпретации первичных результатов. На основе полученных значений мер центральной тенденции можно, например, предвидеть наиболее вероятные результаты аналогичного исследования другой выборки. На основе же мер изменчивости можно оценить точность проведенных измерений, т. е. выявить случайные ошибки измерения. Во-вторых, та или иная из вышеназванных мер необходима для проверки статистической значимости различий (см. с. 274, Приложение I: t-критерий Стьюдента) между результатами исследования двух разных выборок, а также для вычисления так называемых коэффициентов корреляции, о которых сейчас пойдет речь.
Меры взаимосвязи. Коэффициентами корреляции пользуются для того, чтобы выяснить, существует ли взаимосвязь между двумя переменными, и определить ее степень, т. е. тесноту взаимосвязи. Значение коэффициента корреляции изменяется от -1 до +1. Величины, лежащие в этих пределах, отражают максимально возможную взаимосвязь сравниваемых переменных. Когда коэффициент корреляции равен нулю, то это означает, что взаимосвязь отсутствует. Положительная корреляционная связь указывает на прямо пропорциональное отношение между двумя переменными, а отрицательная - на обратно пропорциональную взаимосвязь. Чем больше абсолютное значение коэффициента корреляции, тем теснее связь между изучаемыми переменными. При значениях коэффициентов ± 1 можно говорить об отношении тождественности между переменными.
При сравнении порядковых величин пользуются коэффициентом ранговой корреляции по Ч. Спирмену (r), при сравнении интервальных величин - коэффициентом корреляции произведений по К. Пирсону (r). Рассмотрим кратко способы расчета этих коэффициентов.
Допустим, что с помощью двух опросников (X и Y), требующих альтернативных ответов «да» или «нет», были получены первичные результаты - ответы 15 испытуемых (N =15). Результаты представлены в виде сумм баллов за утвердительные ответы («да») для каждого испытуемого отдельно для опросника Х и опросника Y. Требуется определить, измеряют ли опросники Х и Y похожие личностные качества испытуемых, или не измеряют. Можно предположить, что если опросники по содержанию и формулировкам мало отличаются друг от друга, то сумма баллов, набранная каждым из испытуемых по опроснику X, будет близка к сумме баллов, набранных по опроснику Y.
Полученные в эксперименте первичные результаты представляют собой два ряда порядковых величин для переменной Х и для переменной Y. Для установления взаимосвязи между каждой парой порядковых величин применяют коэффициент порядковой корреляции Спирмена (r). Для расчета величины r известна следующая формула:
r = 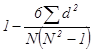 ,
,
где N - число сравниваемых пар величин двух переменных и d2 - квадрат разностей рангов этих величин.
Для вычисления предстоит проделать ряд операций. Прежде всего надлежит табулировать все первичные результаты (табл. 1.1.7). В 1-й графе записывают номер испытуемого, а во 2-й и 3-й - полученные им суммы баллов по первой методике (переменная X) и по второй (переменная Y).
Таблица 1.1.7
Табулирование первичных результатов для расчета коэффициента корреляции по Спирмену ( r)
| Номер испытуемого | X | Y | RX | RY | d | d2 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 47 71 52 48 35 35 41 82 72 56 59 73 60 55 41 | 75 79 85 50 49 59 75 91 102 87 70 92 54 75 68 | 11,0 4,0 9,0 10,0 14,5 14,5 12,5 1,0 3,0 7,0 6,0 2,0 5,0 8,0 12,5 | 8,0 6,0 5,0 14,0 15,0 12,0 8,0 3,0 1,0 4,0 10,0 2,0 13,0 8,0 11,0 | 3,0 2,0 4,0 4,0 0,5 2,5 4,5 2,0 2,0 3,0 4,0 0,0 8,0 0,0 1,5 | 9,00 4,00 16,00 16,00 0,25 6,25 20,25 4,00 4,00 9,00 16,00 0,00 64,00 0,00 2,25 |
|
| åd2 = 71,00 | |||||
Таким образом: r = 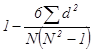 =1-
=1- 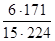 =1-
=1- 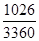 =1-0,305=0,695.
=1-0,305=0,695.
Затем каждому первичному результату присваивают ранг. Эта процедура называется ранжированием. Начинают ее с того, что среди всех значений переменной Х находят наибольшее и в одной строке с ним, но уже в 4-й графе (Rx) проставляют единицу, что и означает 1-й ранг. В нашем случае максимальное число баллов по методике Х получил испытуемый № 8, и поэтому именно его результату следует присвоить 1-й ранг. Затем находят второй по величине результат и в его строке указывают соответственно 2-й ранг. В нашем примере необходимо обратить внимание на следующее: испытуемые № 7 и 15 получили по 41 баллу, а испытуемые № 5 и 6 - по 35 баллов. Для таких случаев принято следующее правило: если в ранжируемом ряду встречаются одинаковые величины, то для них находят среднее значение и считают, что оно определяет ранг как одной, так и другой величины. Следовательно, испытуемым № 7 и 15 надо присвоить одинаковый ранг, а именно 12,5, а испытуемым № 5 и 6 - 14,5, поскольку (12+13):2 =12,5 и (14+15): 2 =14,5. Аналогично осуществляют ранжирование по второй методике, т. е. для переменной У. Заметим, что в данном случае уже трое испытуемых № 1, 7 и 14 получили по одинаковому числу баллов - 75. Первичным результатам этих испытуемых должны были бы быть присвоены 7, 8 и 9-й ранги.
Усреднив эти ранги, каждому испытуемому присваивают одинаковый ранг, в данном случае -8-й.
На следующем этапе табулирования определяют разность рангов для каждой пары значений Х и Y и полученные результаты проставляют в 6-й графе: d =Rx-Ry. Наконец, в 7-й графе отражены значения квадратов разности рангов, т. е. d2 для каждой пары Х и Y. Полученные величины суммируют и записывают в последней строке таблицы: åd2. Полученную величину (в нашем примере åd2 = 171) и подставляют в формулу коэффициента ранговой корреляции.
В нашем примере r = 0,695. Положительное значение полученного коэффициента позволяет утверждать, что оба опросника - Х и Y - дают возможность выявлять похожие, но не идентичные личностные свойства.
Коэффициент корреляции по формуле Пирсона рассчитывается на основе отклонения первичных результатов и среднего квадратичного отклонения от их среднеарифметического значения. Формула расчета коэффициента корреляции по К. Пирсону может быть представлена следующим образом:
rxy = 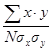 ,
,
где х – отклонение величины Х (первичного результата) от средней арифметической Мх; у - отклонение величины Y (первичного результата) от средней арифметической MY; åx×y - алгебраическая сумма произведений отклонений х и у от Мх и MY; N – объем выборки сравниваемых парпервичных результатов; sх – среднее квадратичное отклонение для первичных результатов Х; sy - среднее квадратичное отклонение для первичных результатов Y.
Рассмотрим пример, который позволит проследить этапы расчета. Допустим, что переменная Х представлена результатами измерения (в сантиметрах) величины коленного рефлекса при инструкции расслабить мышцы; переменная Y – то же, но при инструкции напрячь мышцы (табл. 1.1.8). Проверяется гипотеза о том, что величины коленного рефлекса не взаимосвязаны между собой.
Последовательность расчета коэффициента следующая.
1. По формулам
Мх = 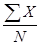 и MY =
и MY = 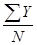
находим средние арифметические значения для переменных Х и Y (в нашем примере Мх =7,5; MY = 8,0).
2. Находим величины отклонений каждого из первичных результатов от Мх и MY - соответственно х и у (см. 4-ю и 5-ю графы).
3. Значение каждого отклонения х и у возводим в квадрат: x2 и у2 (см. 5-ю и 6-ю графы).
Таблица 1.1.8
Расчет коэффициента корреляции по Пирсону ( r)
| Номер пары измерения | X | Y | x | y | x2 | y2 | x×y |
| 1 2 3 4 5 6 7 8 9 10 | 10 8 6 6 13 5 12 10 3 2 | 7 9 11 3 11 7 14 11 6 1 | +2,5 +0,5 -1,5 -1,5 +5,5 -1,5 +4,5 +2,5 -4,5 -5,5 | 1 +1 +3 -5 +3 -1 +6 +3 -2 -7 | 6,25 0,25 2,25 2,25 30,25 6,25 20,25 6,25 20,25 30,25 | 1 1 9 25 9 1 36 9 4 49 | -2,5 +0,5 -4,5 +7,5 +16,5 +2,5 +27,5 +7,5 +9,5 +38,5 |
| å: М: | 75 7,5 | 83 8,0 | 0,0 | 0,0 | 124,50 | 144 | +102,0 |
Таким образом: rXY = 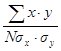 =
= 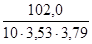 =
= 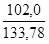 = 0,76.
= 0,76.
4. По формуле для среднего квадратичного отклонения рассчитываем sх иsy (в нашем примере sх =3,53; sy =3,79).
5. Определяем произведения для каждой пары отклонений (см. 8-ю графу).
6. Полученные величины подставляем в формулу коэффициента корреляции по Пирсону. Полученный для нашего примера коэффициент корреляции rXY = 0,76 свидетельствует о том, что обе величины коленного рефлекса взаимосвязаны, несмотря на различные условия их измерения.
Дата: 2018-12-21, просмотров: 387.