Выше неоднократно утверждалось, что развитие у детей логического мышления – это одна из важных задач начального обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам – необходимое условие успешного усвоения учебного материала.
Основная работа для развития логического мышления должна вестись с задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления. Нестандартные логические задачи – отличный инструмент для такого развития. Конкретные примеры логических задач приведены в приложениях 1 и 2. Однако что зачастую наблюдается на практике? Учащимся предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают ее. Но извлекается ли из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учащихся может вновь испытывать затруднения при решении.
Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей:
1. Работа над решенной задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.
2. Решение задач различными способами. Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь это умение свидетельствует о достаточно высоком математическом развитии. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем.
3. Правильно организованный способ анализа задачи - от вопроса или от данных к вопросу.
4. Представление ситуации, описанной в задаче (нарисовать "картинку"). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
5. Самостоятельное составление задач учащимися.
Составить задачу:
Ø используя слова: больше на, столько, сколько, меньше в, на столько больше, на столько меньше;
Ø решаемую в 1, 2, 3 действия;
Ø по данному ее плану решения, действиям и ответу;
Ø по выражению.
6. Решение задач с недостающими данными.
7. Изменение вопроса задачи.
8. Составление различных выражений по данным задачи и объяснение, что означает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
9. Объяснение готового решения задачи.
10. Использование приема сравнения задач и их решений.
11. Запись двух решений на доске - одного верного и другого неверного.
12. Изменение условия задачи так, чтобы задача решалась другим действием.
13. Закончить решение задачи.
14. Какой вопрос и какое действие лишние в решении задачи (или, наоборот, восстановить пропущенный вопрос и действие в задаче).
15. Составление аналогичной задачи с измененными данными.
16. Решение обратных задач.
Систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на развитие логического мышления, организованных согласно приведенной выше схеме, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Глава 2.
Практическая часть.
Как уже было сказано во введении теоретической части нашей работы, умение строить дедуктивные рассуждения (умозаключения) является основным методом математической науки и одним из особых средств усвоения курса математики в средней школе. Это отмечает и Г. В. Дорофеев. Он писал: «Ответственность преподавателей математики особенно велика, так как отдельного предмета «логика» в школе нет, и умение логически мыслить и строить правильные умозаключения необходимо развивать с первых «прикосновений» детей к математике. И то, как этот процесс мы сможем внедрить в различные школьные программы, будет зависеть какое поколение придет нам на смену» [4]
Именно такая позиция легла в основу постановки и проведения практической части нашей работы.
Тема : Обучение построению дедуктивным умозаключениям при решении задач в 4 классе.
Цель: Подтвердить или опровергнуть гипотезу, выдвинутую в теоретической части данной работы. Разработать задания, которые способствовали бы развитию умения строить дедуктивные умозаключения при решении задач, на примере различного математического материала.
Эксперимент проводился в 4 «А» классе. Количество детей: 14 человек. Девочек – 6. Мальчиков – 8.
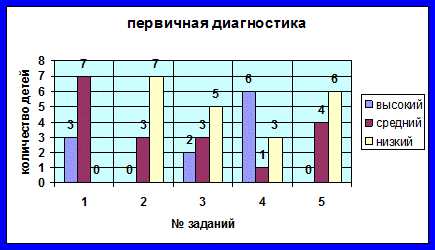
1. Констатирующий этап позволяет нам выявить уровень развития логического мышления у учащихся, выявить показатели сформированности умений, таких как: умения решать нестандартные задачи и выстраивать логические цепочки. Определить приемы активизации творческой мыслительной деятельности с помощью дедуктивных умозаключений на уроках математики у учащихся 4-х классов. Полученные с помощью констатирующего эксперимента данные помогут определить задачи и разработать содержание и методы формирующего этапа исследования:
1. Подготовленные нами варианты работ раздаются учащимся. Работа выполняется в двух аналогичных вариантах (варианты работ см. приложение 4).
2. Учителем дается инструкция к выполнению каждого задания, указывая на то, что последующее будут сложнее предыдущего.
3. Итог: в полученных работах можно выделить 3 уровня (критерии оценивания):
Ø Высокий(5 заданий)
Ø Средний(3-4 задания)
Ø Низкий(меньше 3 заданий)
2. Формирующий этап.
На формирующем этапе своей работы мы ставим следующие задачи:
1. Развивать логическое мышление.
2. Формировать умение строить дедуктивные умозаключения и пользоваться ими на практике.
3. Развивать мыслительные операции (анализ, синтез, сравнение, сопоставление).
Содержание работы.
Ø давать задания с учетом возможностей детей, постепенно усложняя;
Ø перед началом работы детей над тем или иным заданием, давать четкую инструкцию по его выполнению;
Ø контролировать выполнение детьми данных заданий;
Ø осуществлять контроль уровня сформированности умения строить дедуктивные умозаключения.
На данном этапе, на практике реализуется составленная группа заданий, которые способствуют развитию логического мышления, путем построения дедуктивных умозаключений.
3 . Контрольный этап.
На данном этапе эксперимента с классом проводились такие формы работ:
Ø Открытые уроки (содержание уроков см. приложение 5)
Ø Практическая работа с классом (математический диктант).
Ø Практическая работа с классом (см. приложение 3)
Цель : Проверить уровень сформированности умения строить дедуктивные умозаключения у учащихся при решении математических задач.
Математический диктант.
Данный вид работы позволяет учителю быстро и точно определить пробелы в знаниях учащихся. Мы предлагаем математический диктант, который применялся на преддипломной практике.
1
Начни или закончи высказывание:
1. Чтобы узнать, на сколько одно число больше или меньше, чем другое, надо…
2. При умножении единицы на любое число получается…
3. … нуля на любое число получается нуль.
4. Для того чтобы найти скорость, нужно…
5. Для того чтобы найти значение периметра прямоугольника, нужно…
6. … , то значение разности равно нулю.
7. … прибавить вычитаемое, то получится уменьшаемое.
2
1. У Вити и Мити было одинаковое количество гвоздей. Витя отдал Мите 3 гвоздя. Насколько больше гвоздей стало у Мити, чем у Вити?
2. «Вот вам три таблетки, – сказал доктор. – Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?
3. Петров на 8 лет моложе, чем Светлов. Петров на 3 года старше, чем Денисов. Кто моложе всех? На сколько лет Светлов старше Денисова?
3
Вставь такие числа, чтобы неравенства были верными:
__ х 6 > __ х 9
Таким образом, целью данного диктанта является закрепление таких навыков как сравнение значения выражения с числом, нахождение определенной закономерности, умение использовать дедуктивные умозаключения при вычислениях и нахождении логических цепочек.
Проводилось множество диктантов, в течение нашей работы, направленных на закрепление и другого материала, такого как: уравнения, порядок действий. Данный вид работы мы реализовывали, не выходя за рамки курса изучения математики. Работы такого рода служили пропедевтикой по изучаемой нами теме и помогали при достижении поставленных нами целей.
3.1. Итог : проверив работы учащихся, мы сделали вывод о том, что у учащихся формируется навык использования дедуктивных умозаключений при различных видах работ, таких как: составление выражений по условию задачи, навык сравнения выражения с числом, построение логических цепочек. Большинство учащихся допустили ошибки в задании, связанном с расстановкой знаков действий, что говорит о том, что надо как можно больше работать над вариативностью мышления, чтобы научить детей смотреть и видеть на несколько шагов вперед. В приложении 1 и 2 приведены варианты заданий, которые способствовали реализации нашего исследования и приближению нашей цели к реальности.
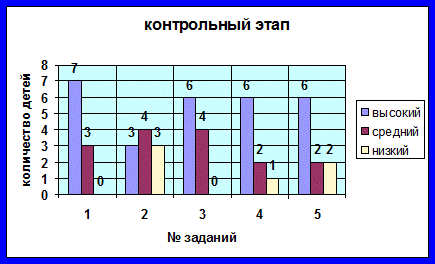
На диаграмме контрольного этапа мы видим, что динамика развития исследуемой проблемы весьма заметна. Если при первичной диагностики с теоретическим материалом справилось 30% учащихся, то после проведенной нами работы этот показатель повысился до 70%, что говорит о правильно подобранных методах и формах работы с детьми. Но, решая нестандартные задачи, учащиеся все еще могут ошибаться и для того, чтобы избежать дальнейших ошибок, нужно постоянно поддерживать интерес детей и развивать их способности.
3.2.Вывод: Констатирующий эксперимент подтвердил положения, выдвинутые в теоретической части данной работы. Большинству учащихся трудно выделять определенные закономерности, выстраивать логические цепочки и решать нестандартные задачи. Поэтому на формирующем этапе нашей работы мы определили группу заданий, решение которых способствовало развитию умения строить дедуктивные умозаключения.
Группа заданий и форма выполнения, предложенных на формирующем этапе (см. приложение 3), вызвали интерес у учащихся. Нужно отметить активность и сознательность учащихся при их выполнении. На наш взгляд, такой активизации способствовали занимательность и наглядность заданий.
При выполнении первых заданий у детей возникли трудности в построении логических цепочек, опираясь на дедуктивные рассуждения. Но в дальнейшем дети стали допускать меньше ошибок при ответах на вопросы и выполнении практических заданий.
Заключение .
Основной целью математического образования должно быть развитие умения математически, а значит, логически и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать умения строить дедуктивные умозаключения при решении на уроках математики различного рода математических задач.
Итак, в своей работе мы исследовали и доказали необходимость использования дедуктивных умозаключений при решении задач. Именно разработав группу заданий, мы сможем улучшить математическую подготовку учащихся, реализуя на практики поставленную нами цель. Организация различных форм работы с задачами поможет нам развивать у детей логическое мышление, с помощью умения строить дедуктивные умозаключения, и математические способности. А так же поможет нам расширить детский кругозор и разрушить стереотипы у детей при решении различного рода задач. Исходя из выше сказанного, мы можем заключить, что действительно, развивать умение строить дедуктивные умозаключения, учить рассуждать и доказывать на уроках математики, возможно при условии использования на уроках системы всевозможных задач, проводя из урока в урок аналитико-синтетическую работу с каждым из заданий. И как мы говорили ранее, систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
В данной работе мы исследовали вопрос возникновения и развития теории дедукции, изучили основные понятия. Рассмотрели психолого-педагогические особенности младших школьников, место и роль дедуктивных умозаключений при решении математических задач. А так же показали пропедевтические задания, которые можно использовать при обучении учащихся строить правильные дедуктивные умозаключения.
Изучив эту проблему, и проанализировав литературу и передовой опыт учителей-новаторов, мы пришли к выводу, что эта тема недостаточно изучена и представлено очень мало практических и методических разработок. В целях совершенствования преподавания математики целесообразна дальнейшая разработка новых методик для развития умения правильно мыслить, рассуждать и доказывать, используя дедуктивные умозаключения. В ходе нашей практики мы увидели необходимость систематического использования на уроках задач, способствующих формированию у учащихся познавательного интереса и самостоятельности. Целесообразно использовать на уроках задачи на сообразительность и задачи-шутки. Учитывая индивидуальные особенности учащихся, мы использовали задания различного типа, осуществляя личностно-ориентированный подход. Осуществляя целенаправленное обучение школьников математике, с помощью специально подобранных упражнений, мы учим их наблюдать, пользоваться аналогией, индукцией, дедукцией, сравнениями и делать соответствующие выводы.
На государственной практике мы выполняли различные по форме и содержанию работы, направленные на реализацию поставленных нами цели и задач. В ходе теоретического и экспериментального исследования получены следующие основные результаты:
Изучив психологические особенности учеников 4 «А» класса, мы выяснили, что целесообразно выбирать в качестве основного содержания работы систему нестандартных заданий.
Результаты, полученные в дипломной работе, позволяют сделать следующие выводы:
1. Разработанная система упражнений для учащихся по развитию умения строить дедуктивные умозаключения при решении задач, обеспечивает достаточную глубину усвоения основных математических понятий.
2. Предложенная система заданий содействует более полному раскрытию связей между различными темами учебного материала.
3. Используемые задания позволяют активизировать творческие способности учащихся при решении математических задач.
4. Рекомендуемая методика позволяет научить детей решать логические задачи, строить дедуктивные умозаключения, разрешать проблемные ситуации и добиваться оригинальности решений.
Таким образом, проведенное нами исследование позволяет утверждать, что гипотеза, выдвинутая нами в теоретической части данного исследования, подтвердилась. Наше исследование показало, что, используя дедуктивные умозаключения при решении задач, мы решаем одну из главных задач, а именно: развиваем логическое мышление школьников, учим детей правильно мыслить, аргументировать и доказывать, что важно, и даже, необходимо. Поиск новых путей активизации творческой деятельности школьников на уроках математики является одной их неотложных задач современной методики математики. Поэтому использование учителем начальной школы наших методических рекомендаций при развитии умения использовать дедукцию при решении математических задач, является не только желательным, но даже необходимым элементом обучения математике. Мы показали, что есть возможность использовать дедуктивные умозаключения в начальных классах, и это даже необходимо, так как именно они воспитывают строгость, четкость и лаконичность мышления.
Список литературы
1. Атахов Р. В. Соотношение общих закономерностей мышления и математического мышления. Вопросы психологии, №5, 1995, С. 46;
2. Гетманова А. Д. Занимательная логика. – М., «Владос», 1998, Ч. 1, С. 171;
3. Гетманова А. Д. Логика. – М., «Добросвет», 2000, С. 137;
4. Дорофеев Г. В. О принципах отбора содержания школьного математического образования. Математика в школе, №6, 1990, С. 2-5;
5. Истомина Н. Б. Методика обучения математике в начальных классах. – М., «Академия», 1998, С. 164;
6. Крутецкий В. А. Психология математических способностей школьников. М., 1968, С. 206-209, 291-293;
7. Кудрявцев Л. Д. Современная математика и ее преподавание. – М., 1980. С. 127;
8. Липина И. Развитие логического мышления на уроках математики // Начальная школа. – 1999. - № 8. С. 37-39.
9. Лехова В. П. Дедуктивные рассуждения в курсе математики начальных классов. – Начальная школа, 1988, № 5, С. 28-31;
10. Пойа Д. Математика и правдоподобные рассуждения. - М., 1975, Т. 1;
11. Саранцев Г. И. Обучение математическим доказательствам в школе. – М., «Просвещение», 2000;
12. Семенов Е. М., Горбунова Е. Д. Развитие мышления на уроках математики. Свердловск, 1966;
13. Скаткин Л. Н. Методика начального обучения математике. – М., «Просвещение», 1972, С. 35;
14. Стойлова Л. П. Математика. –М., «Академия», 1997, С. 96;
15. Стойлова Л. П., Пышкало А. М. Основы начального курса математике. – М., «Просвещение», 1988, С. 32;
16. Столяр А. А. Педагогика математики. – Минск, Вышэйшая школа, 1986;
17. Хинчин А. Я. О воспитательном эффекте уроков математики. Математика как профессия. - М., 1980. С. 36;
Дата: 2018-12-21, просмотров: 322.