Задание:
а) Аналитически отыскать безусловный экстремум функции, используя аппарат необходимых и достаточных условий.
б) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 3 итерации методом градиентного спуска (точность счета - 5 знаков после запятой).
в) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 1 итерацию методом наискорейшего спуска (точность счета - 5 знаков после запятой).
г) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 2 итерации методом сопряженных градиентов (точность счета - 5 знаков после запятой).
д) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 1 итерацию методом Ньютона (точность счета - 5 знаков после запятой).
f(X) = -x2 - 4y2 + 32x + 16y - 24 ® extr
Этап №2 Тема : Методы решения ЗНП при ограничениях типа равенства
Задание:
а) Решить задачу графически.
б) Аналитически отыскать экстремум функции при ограничениях типа равенства, используя аппарат необходимых и достаточных условий (методом множителей Лагранжа).
в) Найти решение задачи методом исключений.
г) Найти решение задачи методом штрафных функций.
f(X) = 4x12 + x22 - 12x1 + 12x2 + 3 ® extr
при ограничении : -x1 + x2 = 4
Этап №3. Тема : Методы решения ЗЛП
Задание:
а) Найти максимум и минимум в задаче графически.
б) Найти максимум и минимум в задаче симплекс-методом
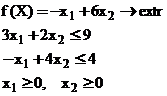
Этап №4. Тема: Методы решения систем линейных алгебраических уравнений
Задание:
а) Решить СЛАУ методом итераций (точность вычислений 0.01).
б) Решить СЛАУ методом Зейделя (точность вычислений 0.01).
x1 - x2 + x3 - 4x4 = 2
2x1 + x2 - 5x3 + x4 = 1
8x1 - x2 - x3 + 2x4 = 9
x1 + 6x2 - 2x3 - 2x4 = -5
Этап №5. Тема: Методы решения алгебраических уравнений
Задание:
а) Отделить все корни алгебраического уравнения. Сделать чертеж.
б) Уточнить наименьший корень алгебраического уравнения методом Ньютона ( точность счета 0.01).
в) Уточнить наименьший корень алгебраического уравнения методом простой итерации (точность счета 0.03).
г) Уточнить наименьший корень алгебраического уравнения методом дихотомии (точность счета 0.03).
x3 + 2x2 - 5x - 6 = 0
Этап №6. Тема : Интерполяция и аппроксимация функций, заданных таблично
Задание:
а) Для функции, заданной таблично, построить интерполяционный полином Лагранжа. Сделать чертеж.
б) Для функции, заданной таблично, построить интерполяционный полином Ньютона. Сделать чертеж.
в) Аппроксимировать функцию полиномами 1-го и 2-го порядка по методу наименьших квадратов. Сделать чертеж.
| x | 1 | 2 | 3 | 4 |
| f(x) | 4 | 10 | 8 | 10 |
РГР по ТО и ЧМ 14 факультет 3 курс (www.dep805.ru/Учраб/Вечерн) Вариант №14
Этап №1 Тема : Методы безусловной минимизации ФМП
Задание:
а) Аналитически отыскать безусловный экстремум функции, используя аппарат необходимых и достаточных условий.
б) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 3 итерации методом градиентного спуска (точность счета - 5 знаков после запятой).
в) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 1 итерацию методом наискорейшего спуска (точность счета - 5 знаков после запятой).
г) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 2 итерации методом сопряженных градиентов (точность счета - 5 знаков после запятой).
д) Из начальной точки с координатами (0, 0) сделать в направлении экстремума 1 итерацию методом Ньютона (точность счета - 5 знаков после запятой).
f(X) = -x2 - 8z2 + x + 8z - 8 ® extr
Этап №2 Тема : Методы решения ЗНП при ограничениях типа равенства
Задание:
а) Решить задачу графически.
б) Аналитически отыскать экстремум функции при ограничениях типа равенства, используя аппарат необходимых и достаточных условий (методом множителей Лагранжа).
в) Найти решение задачи методом исключений.
г) Найти решение задачи методом штрафных функций.
f(X) = 8x12 + x22 + 2x1 - 2x2 + 1 ® extr
при ограничении : 2x1 - x2 = 4
Дата: 2018-09-13, просмотров: 776.