Непосредственное интегрирование – это нахождение неопределенных интегралов с использованием таблицы интегралов и свойств неопределенного интеграла:
1. 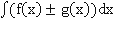 =
= 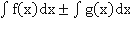
2. 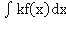 =k
=k 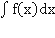 , где k=const
, где k=const
Таблица интегралов
| 1 | 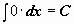
| 11 | 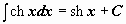
|
| 2 | 
| 12 | 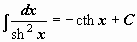
|
| 3 | 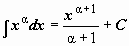 (
( 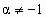 ) )
| 13 | 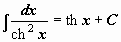 . .
|
| 4 | 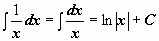
| 14 | 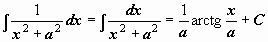
|
| 5 | 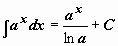 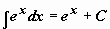
| 15 | 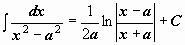
|
| 6 | 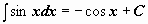
| 16 | 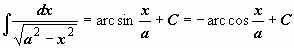
|
| 7 | 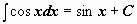
| 17 | 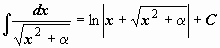
|
| 8 | 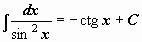
| 18 | 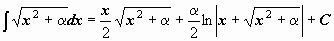
|
| 9 | 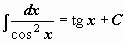
| 19 | 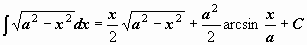
|
| 10 | 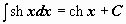
| 20 | 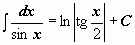
|
| 21 | 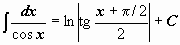
|
Замена переменной в неопределённом интеграле (интегрирование подстановкой).
Пусть 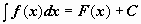 .
.
Тогда 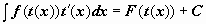 . Здесь t(x) – дифференцируемая монотонная функция.
. Здесь t(x) – дифференцируемая монотонная функция.
При решении задач замену переменной можно выполнить двумя способами.
1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и 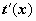 , то замена переменной осуществляется подведением множителя
, то замена переменной осуществляется подведением множителя 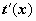 под знак дифференциала:
под знак дифференциала: 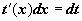 , и задача сводится к вычислению интеграла
, и задача сводится к вычислению интеграла 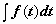 . Например,
. Например, 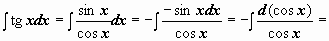 (задача сведена к вычислению
(задача сведена к вычислению 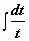 , где t = cos x)
, где t = cos x) 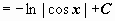 (аналогично находится интеграл от
(аналогично находится интеграл от 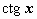 );
); 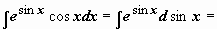 (задача сведена к вычислению
(задача сведена к вычислению 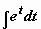 , где t = sin x)
, где t = sin x) 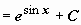 .
.
2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной.
Пример 1 . 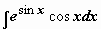
Имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t: 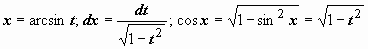
в результате:
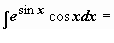
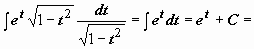
(возвращаемся к исходной переменной)
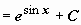 .
.
Пример 2 . 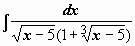 .
.
Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись:
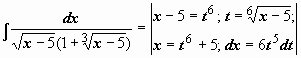 =
= 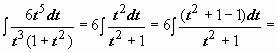
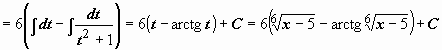
Пример 3 .  (интеграл №19 из табл.).
(интеграл №19 из табл.).
Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: 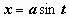 (или
(или 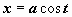 ,
, 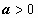 ):
):
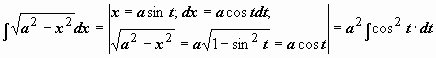 .
.
Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие 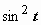 и
и 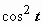 через косинус двойного угла:
через косинус двойного угла: 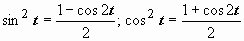 .
.
Поэтому 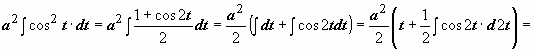
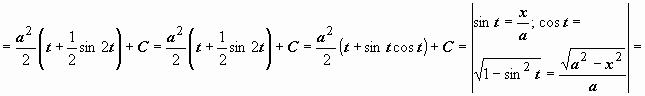
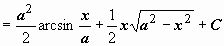 .
.
Пример 4 .
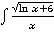 dx=
dx= 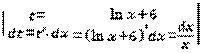 =
= 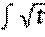 dt=
dt= 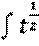 dt=
dt= 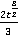 +С=
+С= 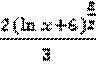 +С
+С
Интегрирование по частям
Производится по формуле: 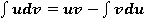
Пример 5 .
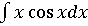 =
= 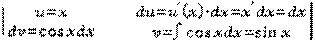 =
=
=x· 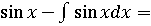 =x·
=x· 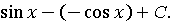
Пример 6 .
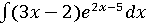 =
= 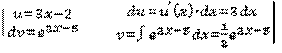 =
=
= 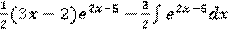 =
= 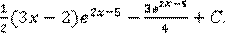
Пример 7 .
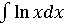 =
= 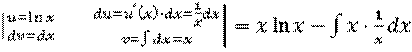 =
=
= 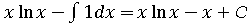 .
.
ЗАДАЧА 6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
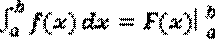 = F ( b )- F ( a )
= F ( b )- F ( a )
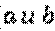 – соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
– соответственно верхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:
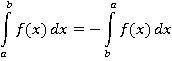
2. Отрезок интегрирования можно разбивать на части:
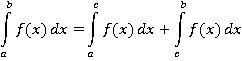
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1 .
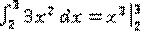 =
=  =27-8=19.
=27-8=19.
Дата: 2018-12-21, просмотров: 315.