1. Вычислить пределы функций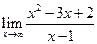 
, 
, 
, 
, 
, 
, 
, 
.
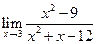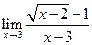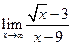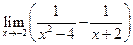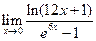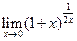2. Указать точки разрыва функций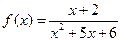 
, 
.
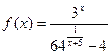3. Установить характер точки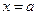 
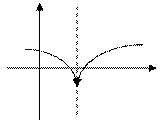
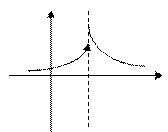
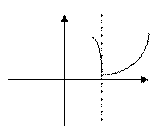
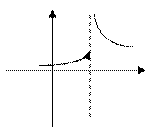1. 2. 3. 4.
Дифференциальное исчисление функции одной переменной
1. Найти производные функций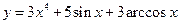 
, 
, 
, 
, 
.
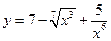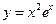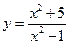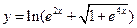2. Найти значение производной функции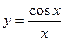 
в точке 
.
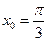3. Найти значение второй производной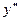 
функции 
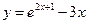в точке 
.
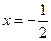4. Изобразить схематично график функции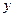 
, для которой выполняются условия 
, 
, 
.
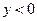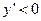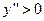Интегральное исчисление функции одной переменной
1. Вычислить интегралы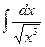 
, 
, 
, 
, 
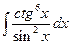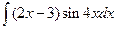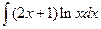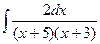
2. Вычислить интеграл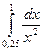 
.
3. Даны интегралы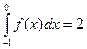 
и 
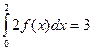. Найти 
.
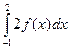4. Даны интегралы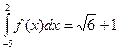 
и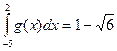 
. Найти значение интеграла 
.
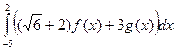Дифференциальные уравнения.
1. Функция 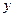является решением дифференциального уравнения 
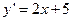, причем 
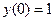. Найти 
.
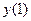2. Найти значение константы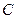 
при решении задачи Коши 
, .
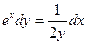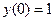3. Решить однородное уравнение первого порядка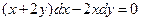 
.
4. Найти общее решение дифференциального уравнения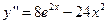 
.
5. Составить характеристическое уравнение однородного дифференциального уравнения с постоянными коэффициентами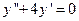 
и найти общее решение.
Контрольная работа по дисциплине «Математика»
для студентов ИДПО направления БУА
Вариант 8.
Комплексные числа
1. Дано число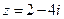 
. Найти 
.
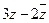3. Даны числа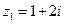 
и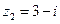 
. Найти 
.
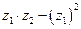5. Найти модуль и аргумент числа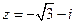 
.
7. Дано число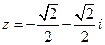 
. Найти 
.
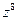9. Дано число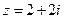 
. Найти корни 
.
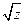Линейная алгебра
1. Даны матрицы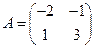 
и 
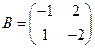. Найти 
.
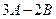2. Найти обратную матрицу для матрицы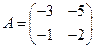 
.
3. Даны матрицы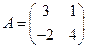 
, 
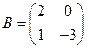и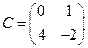 
. Найти произведения 
, 
, 
.
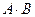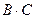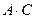4. Вычислить определитель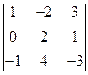 
.
5. Дана система уравнений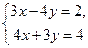 
. Решить ее методом Крамера.
Векторная алгебра
1. Даны векторы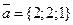 
и 
. Найти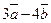 
.
2. Даны векторы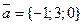 
и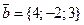 
. Найти скалярное произведение этих векторов.
3. Найти длину векторного произведения векторов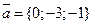 
и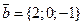 
.
4. Найти площадь параллелограмма, построенного на векторах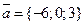 
и 
.
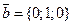5. Найти объем пирамиды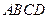 
с вершинами в точках 
, 
, 
, 
.
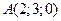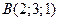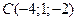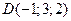Аналитическая геометрия
1. Составить уравнение прямой, проходящей через точк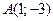и 
и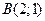 
.
2. Записать уравнение прямой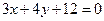 
в отрезках.
3. Найти расстояние от начала координат до прямой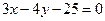 
.
4. Найти нормальный вектор плоскости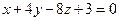 
.
5. Найти уравнение плоскости, проходящей через точку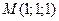 
, параллельно плоскости 
.
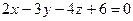Предел и непрерывность функции
1. Вычислить пределы функций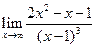 
, 
, 
, 
, 
, 
, 
, 
.
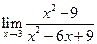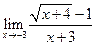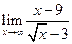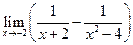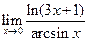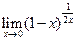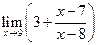2. Указать точки разрыва функции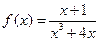 
, 
.
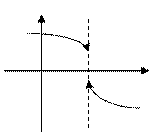3. Установить характер точки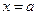
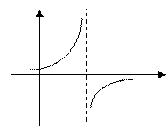
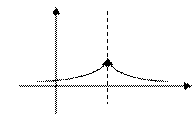1. 2. 3. 4.
Дифференциальное исчисление функции одной переменной
1. Найти производные функций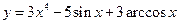 
, 
, 
, 
, 
.
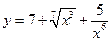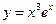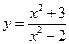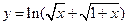2. Найти значение производной функции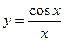 
в точке 
.
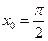3. Найти значение второй производной 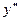функции 
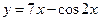в точке 
.
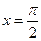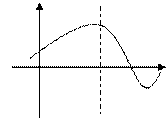
4. Изобразить схематично график функции 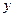, для которой выполняются условия , , 
.
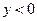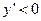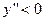Интегральное исчисление функции одной переменной
1. Вычислить интеграл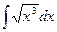 
, 
, 
, 
, 
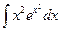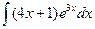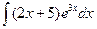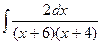
2. Вычислить интеграл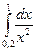 
.
3. Даны интегралы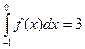 
и 
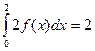. Найти 
.
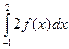4. Даны интегралы 
и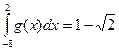 
. Найти значение интеграла 
.
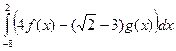Дифференциальные уравнения.
1. Функция 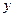является решением дифференциального уравнения 
, причем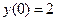 
. Найти 
.
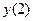2. Найти значение константы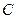 
при решении задачи Коши 
, 
.
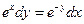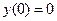3. Решить однородное уравнение первого порядка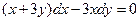 
.
4. Найти общее решение дифференциального уравнения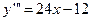 
.
5. Составить характеристическое уравнение однородного дифференциального уравнения с постоянными коэффициентами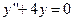 
и найти общее решение.
Контрольная работа по дисциплине «Математика»
для студентов ИДПО направления БУА
Вариант 9.
Комплексные числа
1. Дано число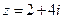 
. Найти 
.
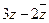2. Даны числа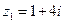 
и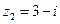 
. Найти 
.
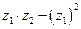3. Найти модуль и аргумент числа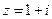 
.
4. Дано число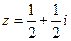 
. Найти 
.
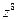5. Дано число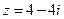 
. Найти корни 
.
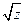Линейная алгебра
1. Даны матрицы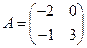 
и 
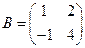. Найти 
.
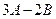2. Найти обратную матрицу для матрицы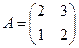 
.
3. Даны матрицы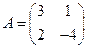 
, 
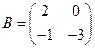и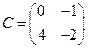 
. Найти произведения 
, 
, 
.
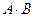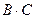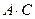4. Вычислить определитель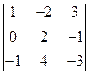 
.
5. Дана система уравнений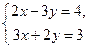 
. Решить ее методом Крамера.
Векторная алгебра
1. Даны векторы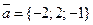 
и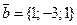 
. Найти 
.
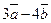2. Даны векторы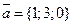 
и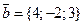 
. Найти скалярное произведение этих векторов.
3. Найти длину векторного произведения векторов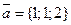 
и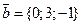 
.
4. Найти площадь треугольника, построенного на векторах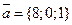 
и 
.
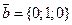5. Найти объем пирамиды 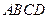с вершинами в точках 
, , 
, 
.
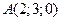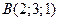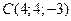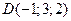Аналитическая геометрия
1. Составить уравнение прямой, проходящей через точк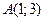и 
и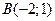 
.
2. Записать уравнение прямой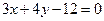 
в отрезках.
3. Найти расстояние от начала координат до прямой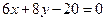 
.
4. Найти нормальный вектор плоскости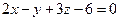 
.
5. Найти уравнение плоскости, проходящей через точку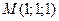 
, параллельно плоскости 
.
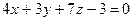Дата: 2018-12-21, просмотров: 225.
