| Температура Т, °С | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Плотность r, кг/м3 | 1000 | 1000 | 998 | 996 | 992 | 988 | 983 | 978 | 972 | 965 | 958 |
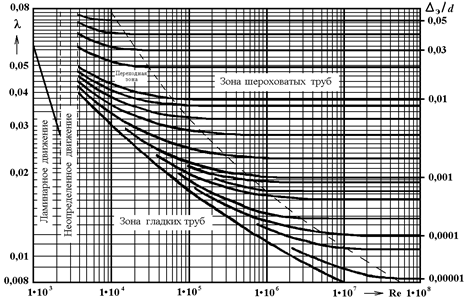
3. Номограмма Кольбрука-Уайта
для определения коэффициента гидравлического трения
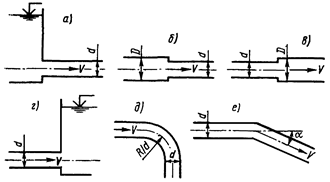
Значения коэффициентов z некоторых местных сопротивлений
47
Продолжение приложения 4
| Тип препятствия | Схема сопротивления по рисунку | Значение коэффициентов z |
| Вход в трубу | а | 0,50 |
| Внезапное сужение | б | 0,50 [ 1 – ( d /D)2] |
| Внезапное расширение | в | [ ( D /d)2 – 1 ]2 |
| Выход из трубы | г | 1 ,0 |
| Плавный поворот (см. схему на рис. д) | Крутой поворот | ||
| d/R | z | a° | z |
| 0 ,20 | 0,14 | 20 | 0,12 |
| 0,40 | 0,21 | 30 | 0,16 |
| 0,60 | 0,44 | 45 | 0,32 |
| 0,80 | 0,98 | 60 | 0,56 |
| – | – | 90 | 1,19 |
Потери давления в некоторых гидравлических элементах
(в местных сопротивлениях)
| Наименование элемента гидропривода | Типоразмер | Номинальный расход Qном, л/мин | Наибольшее рабочее давление р, МПа | Потери давления Dрном, МПа |
| Фильтр пластинчатый | 0,12Г41-11 0,12Г41-12 0,12Г41-13 0,12Г41-14 0,12Г41-15 | 5 12,5 25 50 100 | – – – – – | 0,10 0,10 0,10 0,10 0,10 |
| Распределитель золотниковый с электрическим управлением | ПГ73-11 ПГ73-12 Г72-33 ПГ73-24 ПГ73-25 | 8 20 40 80 160 | 20 20 20 20 20 | 0,20 0,10 0,10 0,30 0,10 |
48
Характеристики некоторых центробежных насосов
| № насоса | Параметры и их единицы | Числовые значения | ||||
| 1 | Q , л/с H , м h , % | 0 20,0 0 | 1,6 20,3 44,0 | 3,0 17,4 55,5 | 3,9 14,5 53,0 | 4,5 12,0 47,0 |
| 2 | Q , л/с H , м h , % | 0 33,7 0 | 2,0 34,5 45,0 | 5,5 30,8 64,0 | 8,3 24,0 63,5 | 10,0 19,0 58,0 |
| 3 | Q , л/с H , м h , % | 0 20,0 0 | 3,0 21,0 56,0 | 5,5 18,5 68,0 | 6,1 17,5 66,0 | 7,0 16,0 60,0 |
| 4 | Q , л/с H , м h , % | 0 62,0 0 | 4,0 64,0 35,0 | 8,3 62,0 54,4 | 16,7 50,0 66,3 | 19,5 44,5 63,0 |
| 5 | Q , л/с H , м h , % | 0 34,0 0 | 4,0 35,2 40,0 | 8,3 34,8 62,0 | 12,5 31,0 71,0 | 15,0 27,0 71,5 |
| 6 | Q , л/с H , м h , % | 0 62,0 0 | 10,0 63,0 48,0 | 19,4 59,0 65,5 | 25,0 54,9 71,0 | 33,4 43,0 66,0 |
| 7 | Q , л/с H , м h , % | 0 37,0 0 | 10,0 39,0 53,0 | 18,0 37,7 72,0 | 25,0 34,6 78,0 | 33,4 28,0 74,5 |
7. Программа для определения диаметра простого трубопровода
Уравнение Бернулли для двух выбранных сечений, считая a1 = a2, можно написать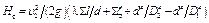 
,
где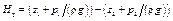 
– располагаемый напор (HS)*, м;
u – средняя скорость в трубопроводе (V), м/с; l – коэффициент гидравлического трения (LAMDA); Sl – общая длина (SUML), м; d – определяемый диаметр (D), м; S z – сумма коэффициентов местных сопротивлений (SUMDZE);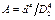 
– коэффициент; D2 – диаметр второго сечения (D 2), м; 
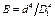– коэффициент; D1 – диаметр первого сечения (D 1), м.
Необходимые для выполнения расчета другие величины обозначены: Q – расход (Q), м3/с; Dн – начальный диаметр трубопровода (D Р), м; n – кинематическая вязкость (NI), м2/с;
Dэ – эквивалентная шероховатость (DELTAE), м;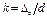 
– относительная шероховатость (K); Rе – число Рейнольдса (R Е). На рис. 33 приводится полный текст программы, написанный на языке FORTRAN, для ЭВМ СМ-4.
___________
* Обозначение величины в программе
49
0001 REAL K, LAMBDA, NI
0002 TYPE 2
0003 2 FORMAT (‘ВВЕДИТЕ Q, HS, DP, D1, D2, SUML, SUMDZE, NI, DELTAE’)
0004 ACCEPT 3, Q, HS, DP, D1, D2, SUML, SUMDZE, NI, DELTAE
0005 3 FORMAT (9F10.7)
0006 PRINT 4
0007 4 FORMAT (10X, ‘ОПРЕДЕЛЕНИЕ ДИАМЕТРА’//)
0008 N=0
0009 D=DP
0010 7 K=DELTAE/D
0011 V=4*Q/(3.24*D*D)
0012 RE=V*D/NI
0013 IF (RE.GE.4000.) GOTO 5
0014 IF (RE.GT.2320.) GOTO 6
0015 LAMBDA=64./RE
0016 GOTO 8
0017 6 D=D+DP
0018 N=N+1
0019 GOTO 7
0020 5 LAMBDA=0.11*(((68./RE)+K)**0.25)
0021 8 IF (DL.EQ.0.) GOTO 15
0022 B=(D/DL)**4
0023 GOTO 16
0024 15 B=1
0025 16 IF (D2.EQ.0) GOTO 17
0026 A=(D/D2)
0027 GOTO 18
0028 17 A=1
0029 18 H=(V*V/19.62)*(LAMBDA*SUML/D+SUMDZE+A-B)
0030 IF (H.GT.HS) GOTO 9
0031 PRINT 10, Q, HS, D1, D2, D, V, RE, LAMBDA, H, N
0032 10 FORMAT (10X, ‘ДАНО:Q’, = F8.6, 12X, ‘HS=’, F6, 1, 3X, ‘, ‘D1=’, F5.3, 10X,
‘D2=’, F5.3, 10X, ‘ОПРЕДЕЛЕНО:D=’, 15.3, ‘V=’, F6.3, 10X, ‘RE=’, F9.1, 13X,
‘LAMBDA=’, F7.5, 2X, ‘H=’, F6.1, ‘N=’, 13)
0033 STOP
0034 9 D=D+DP
0035 N=N+1
0036 GOTO 7
0037 END
Рис. 33
50
Дата: 2018-12-21, просмотров: 584.
