В области нарушения верхней границы закона Дарси необходимо использовать степенной или двухчленный законы фильтрации. В целях общности рассмотрим фильтрацию при степенном законе для случая плоско-радиального течения

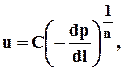                                                                                       64

где C, n - постоянные, 1 £ n £ 2. n=2 – соотвествует закону Краснопольского

ПРИТОК НЕФТИ В ПОРИСТОМ ПЛАСТЕ

Совокупность пьезометрических кривых , отвечающих как хак закону фильтрации Дарси, так и всем возможным отклонениям от этого закона, ограничена предельными кривыми, с одной стороны, кривой, отвечающей закону Дарси, с другой стороны, отвечающей закону Краснопольского (рис. 34), Все остальные кривые нашей совокуппности будут занимать промежуточное место между двумя предельными. Из указанных кривых наименее крутой подъём (у стенки скважины) имеет кривая логарифмического типа, соответствующая закону Дарси.

При фильтрации по нелинейному закону фильтрации индикаторная линия не может быть прямой (рис.35).

Для закона Краснпольского выражение для дебита имеет вид

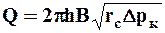,                                                                            65

где В – некоторая константа.

Соответствующая индикаторная кривая – парабола.

Возможны составные индикаторные зависимости в случае прохождения фильтрации жидкости по разным законам, н. п. начальный прямолинейный участок (закон Дарси) и собственно кривая (нелинейный закон).

Коэффициент продуктивности при фильтрации по нелинейному закону численно равен тангесу угла наклона хорды, проведённой через начало координат и данную точку индикаторной кривой, к оси перепадов давления D р_к. Так как индикаторная кривая обращена выпуклостью в сторону оси дебитов, то этот коэффициент уменьшается с увеличением дебитов.

ЧАСТНЫЕ ИНДИКАТОРНЫЕ ЗАВИСИМОСТИ

ДВУХЧЛЕННАЯ

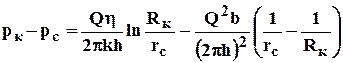.                                          66

Дебит находится как положительный корень квадратного уравнения (66).

ВОГЕЛЯ

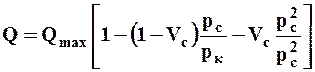,                                                  67

где Q_max – максимально возможный дебит при р_с ® 0; V_c- константа Вогеля.

ФЕДКОВИЧА

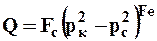,                                                                                  68

где F_c , Fe –константы Федковича.

ВЛИЯНИЕ РАДИУСА СКВАЖИНЫ НА ЕЁ ПРОИЗВОДИТЕЛЬНОСТЬ

Определим дебит в двух крайних случаях: по закону Дарси и по закону Краснопольского развитого нелинейного течения . Тоже самое сделаем и в случае радиально-сферического течения. Если примем радиус одной скважины r_с, а другой - r_c^/= xr_c и, соответственно, дебиты G и G^/, а их отношение обозначим через у=G/G^/, то получим следующие формулы для вычисления предельных значений у

Тип потока

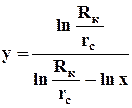
Из таблицы видно, что при сохранении закона Дарси в плоско-радиальном потоке влияние радиуса скважины на дебит невелико (необходимо увеличение радиуса в 10 раз, чтобы дебит вырос на 20%). Если же фильтрация нелинейна, то влияние r_c на G усиливается. Для сферически-радиального потока дебит скважины зависит от радиуса в большей степени, особенно при нелинейном законе фильтрации. Таким образом, расширение забоя скважины способствует увеличению производительности. При торпедировании забоя, гидравлическом разрыве пласта и других способах воздействия на призабойную зону образуются и расширяются трещины, что способствует нарушению закона Дарси и, следовательно, усилению влияния радиуса скважины на приток к ней жидкости.