VI . УСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ОДНОРОДНОЙ
СЖИМАЕМОЙ (УПРУГОЙ) ЖИДКОСТИ И ГАЗА
1. Дифференциальные уравнения установившейся фильтрации
упругой жидкости и газа по закону Дарси
Составим дифференциальное уравнение фильтрации однородного сжимаемого флюида в однородной пористой среде на основе уравнения неразрывности потока (2.11)
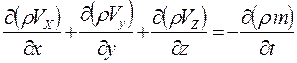(6.1)
и уравнений движения (2.4)
, 
, 
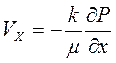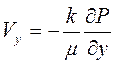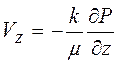, (6.2)
т.е. считаем фильтрацию сжимаемого флюида r=r(Р) по закону Дарси, процесс изотермический (Т=const), при этом вязкость флюида и проницаемость зависят от давления , т.е. m=m(Р) и k=k(Р).
Введем обобщенную функцию давления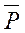 
следующим образом. Примем, что ее дифференциал
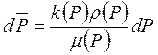, (6.3)
тогда
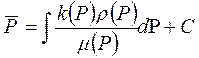(6.4.)
будем называть обобщенной функцией Лейбензона.
Так как функция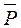 
и давление Р зависят от координат и времени, то равенство (6.3) можно записать в следующем развернутом виде, используя понятие полного дифференциала функции от многих переменных:
.
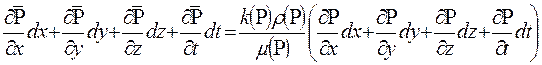Из сравнения коэффициентов при dx, dy, dz, dt получаем
; 
; 
;
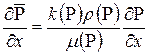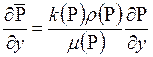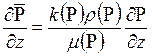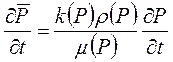. (6.5)
Запишем выражения для массовых скоростей фильтрации с использованием (6.5)
; 
;
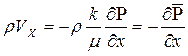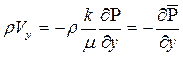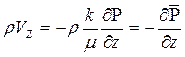. (6.6)
Далее, подставив (6.6) в уравнение неразрывности (6.1). получим
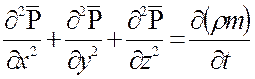(6.7)
или 
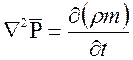(6.8)
- это и есть дифференциальное уравнение неустановившегося движения однородного флюида в однородной пористой среде по закону Дарси.
В случае установившейся фильтрации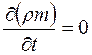 
и уравнение (6.7) принимает вид
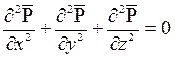, (6.9)
или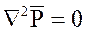 
, (6.10)
т.е. при установившейся фильтрации обобщенная функция Лейбензона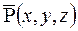 
удовлетворяет уравнению Лапласа.
Установившаяся фильтрация упругой жидкости
Прежде всего найдем выражение функции Лейбензона для упругой (слабо сжимаемой) жидкости, описываемой уравнением состояния (2.14):
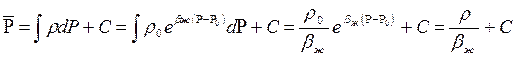. (6.15)
Если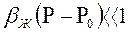 
, то можно взять уравнения состояния упругой жидкости в виде (2.15). Тогда из (6.15) получаем следующее выражение для функции Лейбензона
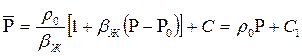. (6.16)
Подставив (6.16) в дифференциальное уравнение (6.9), получим
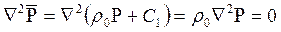. (6.17)
Как следует из выражения (6.17), при установившейся фильтрации упругой жидкости плотность можно считать постоянной, поэтому при решении практических задач с установившейся фильтрацией упругой жидкости можно пользоваться формулами для установившейся фильтрации несжимаемой жидкости. Однако в случае фильтрации упругой жидкости в пласте с очень высоким пластовым давлением и при большой депрессии, следует использовать функцию Лейбензона (6.15), поскольку возможны большие погрешности.
Прямолинейно-параллельный фильтрационный поток
Идеального газа
На основании уравнения состояния идеального газа (2.18)
,
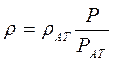при изотермическом процессе, находим функцию Лейбензона
.
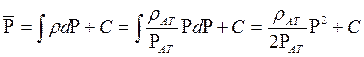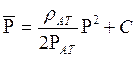. (6.18)
Используя аналогию между течением несжимаемой жидкости и течением газа найдем характеристики фильтрационного потока газа по аналогии с соответствующими характеристиками потока несжимаемой жидкости.
1) Распределение давления в прямолинейно-параллельном фильтрационном потоке (рис.8) несжимаемой жидкости
.
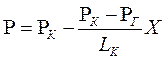При фильтрации газа аналогичное соотношение справедливо для функции Лейбензона:
.
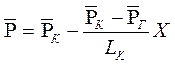Используя выражение функции Лейбензона (6.18)
; 
,
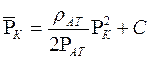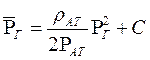находим распределение давления Р(х) в прямолинейно-параллельном потоке идеального газа
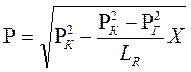, (6.19)
 |
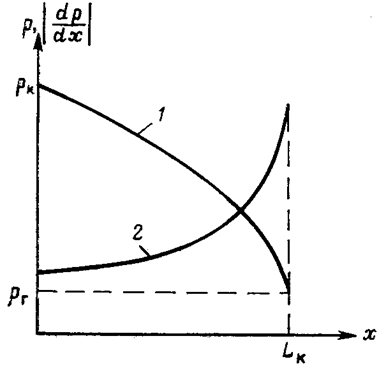т.е. давление по длине пласта Р(х) изменяется по параболическому закону (рис.36, кривая 1), а зависимость Р2(х) – прямолинейная.
Рис. 36
2) Градиент давления в потоке несжимаемой жидкости имеет вид
.
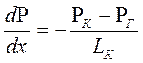По аналогии градиент функции Лейбензона для потока газа будет
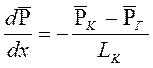. (6.20)
Дифференцируя по Х выражение (6.18) и используя выражения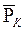 
и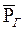 
, из уравнения (6.20) получим распределение градиента давления в фильтрационном потоке газа
,
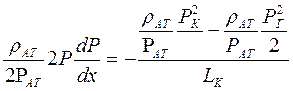откуда
, 
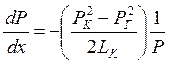(6.21)
где Р – определяется по формуле (6.19).
График распределения градиента давления в потоке газа представлен на рис. 36, кривая 2. Градиент давления возрастает при приближении к галереи.
3) Объемный расход несжимаемой жидкости в рассматриваемом одномерном потоке
.
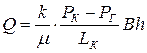Заменяя объемный расход Q массовым расходом Qm и давление Р функцией Лейбензона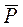 
, получим
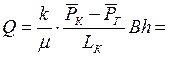
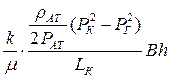. (6.22)
Тогда объемный расход газа, приведенный к атмосферному давлению, выражается формулой
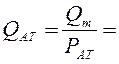
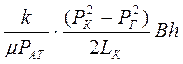. (6.23)
4) Вместо скорости фильтрации для несжимаемой жидкости
.
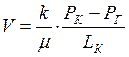при фильтрации газа аналогично определяется массовая скорость фильтрации , т.е.
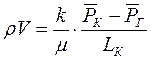или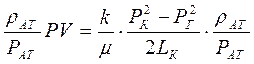 
,
откуда
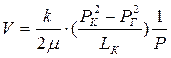. (6.24)
График функции V(x) аналогичен графику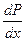 
. Возрастание V(x) происходит за счет расширения газа при снижении давления.
5) Средневзвешенное по объему порового пространства, занятого
газом, пластовое давление
.
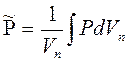В нашем случае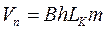 
; dVп=Bhmdx .
Тогда
.
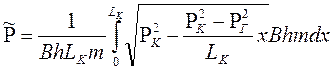После интегрирования получим
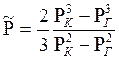. (6.25)
VI . УСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ОДНОРОДНОЙ
СЖИМАЕМОЙ (УПРУГОЙ) ЖИДКОСТИ И ГАЗА
1. Дифференциальные уравнения установившейся фильтрации
упругой жидкости и газа по закону Дарси
Составим дифференциальное уравнение фильтрации однородного сжимаемого флюида в однородной пористой среде на основе уравнения неразрывности потока (2.11)
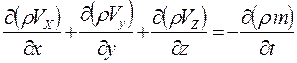(6.1)
и уравнений движения (2.4)
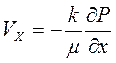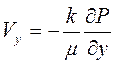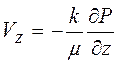, , , (6.2)
т.е. считаем фильтрацию сжимаемого флюида r=r(Р) по закону Дарси, процесс изотермический (Т=const), при этом вязкость флюида и проницаемость зависят от давления , т.е. m=m(Р) и k=k(Р).
Введем обобщенную функцию давления 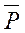следующим образом. Примем, что ее дифференциал
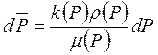, (6.3)
тогда
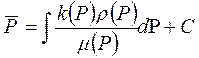(6.4.)
будем называть обобщенной функцией Лейбензона.
Так как функция 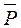и давление Р зависят от координат и времени, то равенство (6.3) можно записать в следующем развернутом виде, используя понятие полного дифференциала функции от многих переменных:
.
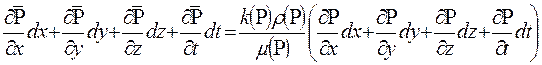Из сравнения коэффициентов при dx, dy, dz, dt получаем
; ; ;
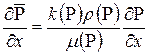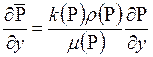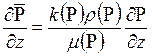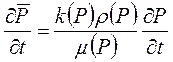. (6.5)
Запишем выражения для массовых скоростей фильтрации с использованием (6.5)
; ;
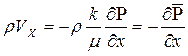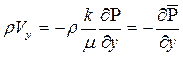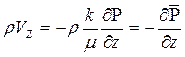. (6.6)
Дата: 2018-12-21, просмотров: 456.
