СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ.. 5
ЗАДАНИЯ ДЛЯ ДОМАШНИХ КОНТРОЛЬНЫХ РАБОТ. 21
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 31
ВВЕДЕНИЕ
Целью преподавания дисциплины «математика» состоит в ознакомлении студентов данного направления с основными понятиями, положениями и методами математики. Дисциплина «Высшая математика» формирует базовые знания и кругозор, необходимые для освоения обще-профессиональных и специальных дисциплин. Данный курс способствует созданию условий для формирования профессиональных навыков будущего специалиста.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Раздел 1 Элементы линейной и векторной алгебры
Тема 1. 2 Система линейных уравнений
Система n линейных уравнений с n переменными (общий вид). Матричная форма записи системы. Совместные и несовместные, определенные и неопределенные системы. Теорема Крамера о разрешимости системы n линейных уравнений с n переменными (без доказательства). Решение системы по формулам Крамера, с помощью обратной, методом Гаусса. (1, гл. 2, §2.1-2.3,2.6; с. 38-47,53-56); (2, гл. 2).
При изучении материала темы следует освоить матричную форму записи заданной системы п линейных уравнений с п переменными и уметь переходить к этой форме от общего вида системы и наоборот. Необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными. Решить систему линейных уравнений помогает метод Гаусса, теорема Крамера и обратная матрица. Отметим, что формулы Крамера и обратная матрица, работают не всегда, а лишь в том случае, когда определитель матрицы коэффициентов при неизвестных не равен нулю. (см. примеры 2.1–2.3, 2.6, 2.7).
Наиболее важен для практики метод Гаусса, имеющий по сравнению с другими способами решения ряд достоинств: он менее трудоемок, позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число ее независимых уравнений и исключить «лишние».
Отметим, что системы линейных уравнений с большим числом неизвестных (более 3), решаются в основном методом Гаусса.
В методе Гаусса нужно усвоить правило исключения неизвестных x1, x2, …, xn. Цель – в первом столбце во всех строках кроме первой получить нули путем прибавления первой строки, умноженной на подходящие коэффициенты, ко второй и последующим строкам.
Затем умножается вторая строка на соответствующие коэффициенты. Цель – обеспечить нули во втором столбце во всех строках кроме второй (a22 ¹0) путем прибавления к третьей и последующим строкам второй строки, умноженной на необходимые коэффициенты и т.д.
Для первой строки это коэффициенты (-a21/a11;-a31/a11;…;-am1/a11); для второй строки это коэффициенты (-a32/a22;-a42/a22;…;-am2/a22).
Множество всех переменных делятся на два класса – главные или базисные переменными, для которых определитель матрицы из коэффициентов при них отличен от нуля (переменные x1, x2,…, xr), и свободные, остальные (n–r) переменных. Основная задача – выразить главные переменные через свободные.
При прямом ходе метода Гаусса решения системы линейных уравнений определяется главная переменная xr. Затем при обратном ходе определяются остальные главные переменные xr-1, xr-2 и так до x1.
Необходимо разобраться (теорема Кронекера-Капелли) в том, что система имеет единственное решение в том случае, когда ранг матрицы «r» равен числу переменных «n», т.е. r=n; система имеет бесконечное множество решений, если n >r.
Рекомендуется разобрать задачи с решениями № 2.1–2.3, 2.6, 2.7 и задачи для самостоятельной работы № 2.11, 2.12, 2.15–2.18, 2.21–2.23 по учебнику [1] и аналогичные задачи по практикуму [2].
Раздел 3 Введение в анализ
Тема 3.1 Функции
Понятие о множествах. Действительные числа и числовые множества. Постоянные и переменные величины. Функции и способы их задания. Область определения функции. Четные, нечетные, монотонные и ограниченные функции. Сложная функция. Понятие элементарной функции. Основные элементарные функции и их графики. Неявные функции. (гл. 4, § 4.1–4.3, 4.6; с. 95–99, 100–103, 115–117); (2, гл. 5,4).
Прежде всего, полезно ознакомиться с некоторыми логическими символами и кванторами, чтобы использовать их в дальнейшем для сокращения записей (1, с. 123).
Изучение темы следует начать с основных понятий теории множеств, [1, с. 123–124]. Далее нужно четко усвоить важнейшее понятие математического анализа – функции, уметь находить область ее определения, знать три способа задания функции: аналитический, графический, табличный.
Студенту нужно знать простейшие преобразования для построения функций, как-то: сдвиг графика y=f(x+a)+b вправо при а < 0 и влево при a > 0, а также на 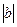 параллельно оси Ох вниз при b< 0 и вверх на
параллельно оси Ох вниз при b< 0 и вверх на 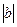 при b >0; сжатие 0<m<1 (растяжение m >1) графика функции y=m×f(x) вдоль оси Ох.
при b >0; сжатие 0<m<1 (растяжение m >1) графика функции y=m×f(x) вдоль оси Ох.
В курсе рассматриваются в основном элементарные функции. Студент должен уяснить определение элементарной функции (1, с. 132) четко знать свойства и строить графики следующих основных элементарных функций: у = С (постоянная), у = xn (степенная), у =ax (показательная), у =logax (логарифмическая). Необходимо усвоить понятие сложной функции (функции от функции).
Построение графика четной (нечетной) функции можно значительно упростить, если учесть, что графики четных функций симметричны относительно оси Оу, а нечетных – относительно начала координат. Одним из характерных свойств функции является монотонность (т.е. возрастание или убывание на каком-либо промежутке).
Студенту необходимо уяснить, что функции находит широкое применение в экономической теории. Знать конкретные виды функций и их сущность (функция полезности, функция издержек и т.д.).
Уравнение линии на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой. Уравнение прямой, проходящей через данную точку в заданном направлении, через две данные точки. Условия параллельности и перпендикулярности двух прямых. Точка пересечения двух прямых. (1, гл. 5, § 5.1–5.5, 5.7, с. 123–132, 138, 139).
Студенту необходимо прочно усвоить материал, который будет использован при изучении экономико-математических методов и прикладных моделей (линейное программирование). Большое значение здесь имеет определение уравнения линии на плоскости как уравнения с двумя переменными х и у, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на ней. Из этого определения следуют два важных для практики положения, которые нужно знать:
1. Если задано уравнение линии, то можно установить, принадлежит ли ей какая-либо точка плоскости. Для этого достаточно подставить координаты точки в уравнение линии вместо переменных х и у. Если окажется, что они удовлетворяют уравнению, то точка принадлежит линии, в противном случае – не принадлежит.
2. Координаты точки пересечения двух линий, заданных своими уравнениями, удовлетворяют обоим уравнениям. Поэтому для нахождения координат точки пересечения двух линий нужно решить систему, составленную из их уравнений. Этот вопрос должен быть усвоен твердо.
Студент должен знать простейшие виды уравнений прямой и уметь пользоваться ими при решении задач. Соответствующий учебный материал приведен в (1, с.95–99, 100–103,115–116).
Обратите особое внимание на нахождение уравнений прямых, параллельной и перпендикулярной данной прямой (пример 4.5).
Рекомендуется разобрать задачи с решениями N4.1–4.3, 4.5, 4.10, 4.12 и задачи для самостоятельного решения N 4.14–4.19, 4.21–4.23 по учебнику (1) и аналогичные задачи по практикуму (2).
Тема 5.1 Производная
Задачи, приводящие к понятию производной. Производная, ее геометрический, механический и экономический смысл. Уравнение касательной к плоской кривой; Дифференцируемость функции. Связь между дифференцируемостью и непрерывностью функции (необходимый признак дифференцируемости). Основные правила и основные формулы дифференцирования. Производная сложной функции Производные высших порядков. (1, гл. 7, § 7.1–7.7, с. 176–205); (2, гл. 7).
Необходимо изучить задачи, приводящие к понятию производной: задачи о касательной и задачи о скорости движения (1, с.176, 177), задачи о производительности труда (экономический смысл производной).
После этого нужно усвоить определение производной как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю. Нужно знать обозначение производной, алгоритм ее вычисления, основываясь на теории пределов.
Студент обязан понимать геометрический и механический смысл производной (1, с.178, 181), уметь решать простейшие задачи по вычислению производной на основе алгоритма ее вычисления; знать и уметь применять основные правила дифференцирования, вычислять производную сложной и обратной функций. При этом нужно знать четко правила вычисления элементарных функций (1,с. 188, 193), знать наизусть таблицу производных (1, с.192). Это позволит усвоить дифференцирование сложных функций, обратных функций, неявно заданных функций (1, с.193), находить производные от произведения, суммы, разности, а также вычислять производные высших порядков. Нужно знать использование понятия производной в экономике, понятие эластичности функции, свойства эластичности функции.
Изучая материал этой темы, студенты знакомятся с необходимым условием дифференцируемости функции. Необходимо четко уяснить, что из дифференцируемости функции в некоторой точке следует ее непрерывность в этой точке. Обратная теорема несправедлива, так как существуют непрерывные функции, которые в некоторых точках могут не иметь производной (1, с. 179, 180).
Рекомендуется разобрать задачи с решениями N 7.1–7.8, 7.10, 7.13, 1.15–7.17 и задачи для самостоятельной работы N 7.20–7.29, 7.35, 7 42, 7.43, 7.46–7.49 по учебнику (1) и аналогичные задачи по практикуму (2).
Для усвоения темы нужно решить задачи контрольной работы, ответить письменно на теоретические вопросы в контрольной работе.
Тема 5 Дифференциал функции
Студенту нужно разобраться с определением дифференциала функции и четко уяснить, что дифференциал функции (1,с.244) – главная линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной.
dy=f¢(x)Dx
Необходимо уяснить геометрический смысл дифференциала (1, с.245).
Дифференциал функции – есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х – получает приращение Dх.
Операция нахождения дифференциала сводится к нахождению производной и также называется дифференцированием функции.
Студенту необходимо уяснить сущность инвариантности формы дифференциала. Для этого нужно понять, что dy=f¢(x)dx и dy=f¢(u)du (1, с.246), если y=f(u), а u=j(x). Тогда по правилу дифференцирования сложной функции y¢=f¢(u)u¢, а u¢dx=du (1, с.244, формула 9.2) и dу=f¢(x)dx=f¢(u)u¢dx=f¢(u)du.
Вид формы (инвариантность формы – это независимость формы от дифференцируемой функции) дифференциала не меняется от характера дифференцируемой функции.
Весьма важным является практическое приложение дифференциала для приближенных вычислений. Необходимо уяснить из геометрического смысла дифференциала, что чем «круче» график функции, тем меньше нужно брать приращение аргумента Dх для вычисления функции с заданной точностью.
Необходимо разобрать задачи N9.1–9.3, 9.5–9.12 (1, с. 244–250) и аналогичные задачи по практикуму (2). При этом нужно понять, что последующее значение функции (1, с.247, пример 9.3) можно вычислять через предыдущее. Если предыдущее значение f(x)= 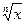 , а последующее f(x+Dx)=
, а последующее f(x+Dx)= 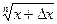 , то
, то 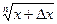 »
» 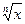 +
+ 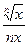 ×D x .
×D x . 
Это так, ибо Dy= 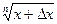 –
– 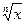
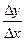
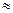
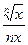 =f¢(x). Поэтому цепочка вычислений такова. Вычисляется предыдущее значение функции, а затем последующее. Чем меньше шаг по приращению аргумента х, тем больше точность вычисления функции.
=f¢(x). Поэтому цепочка вычислений такова. Вычисляется предыдущее значение функции, а затем последующее. Чем меньше шаг по приращению аргумента х, тем больше точность вычисления функции.
На вычислении дифференциала основаны многие численные методы в математике.
Студенту необходимо разобраться в вычислении относительной погрешности через дифференциал (1, с.247, 248) и эластичность функции (1, с.196) Ex(y)=x(y¢)/y.
Номер варианта соответствует начальной букве фамилии студента.
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| У, Ш | Восьмой |
| Д, К, П | Девятый |
| Ф, Щ, Я | Десятый |
ЗАДАНИЯ ДЛЯ ДОМАШНИХ КОНТРОЛЬНЫХ РАБОТ
ВАРИАНТ №1
Задание №1. Найти матрицу С, если: С=АТВ-2ВТ, А= 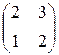 , В=
, В= 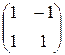 .
.
Задание №2. Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 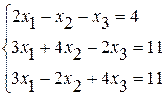
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,3); В (1,3); С (-6,-4).
Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: 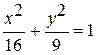
Задание №5 Составить уравнение цилиндра, если ось коллинеарна вектору q(1,2,3), а направляющая задана уравнениями у2 = 4х, z = 0.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы
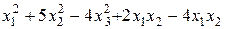 .
.
Задание № 7 Вычислить пределы: 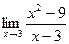 ;
; 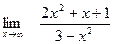
Задание № 8 Найти производные функций:
1. 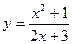 2.
2. 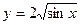
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции у = х3-3х + 5 в точке х0 = 2.
Задание № 10 Исследовать функцию с помощью производных и построить график:
у=2х3 + 3х2 + 1
ВАРИАНТ №2
Задание №1 Найти матрицу С, если: С=АВТ-АТ, А= 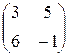 , В=
, В= 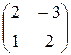
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 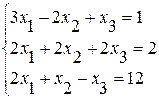
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,1); В (-3,3); С (-5,-2).
Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: 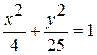
Задание №5 Составить уравнение цилиндра, если ось коллинеарна вектору q(1,1,1), а направляющая задана уравнениями х2 + у2 +z2=0, z=0.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы
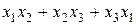 .
.
Задание № 7 Вычислить пределы: 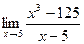 ;
; 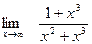
Задание № 8 Найти производные функций:
1. 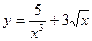 2.
2. 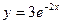
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 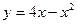 в точке
в точке 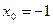 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
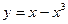
ВАРИАНТ №3
Задание №1 Найти матрицу С, если: С=АТВ-ВАТ, А= 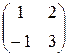 , В=
, В= 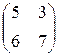 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 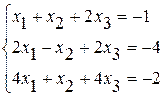
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,2); В (-2,3); С (-2,-3).
Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: 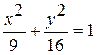
Задание №5 Составить уравнение поверхности, образованной вращением прямой
z = у, х = 0 вращением вокруг оси Oz.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
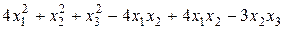
Задание № 7 Вычислить пределы: 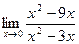 ;
; 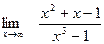
Задание № 8 Найти производные функций:
1. 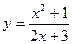 2
2 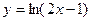
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 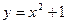 в точке
в точке 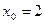 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
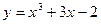
ВАРИАНТ №4
Задание №1 Найти матрицу С, если: С=АВТ-3В, А= 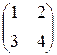 , В=
, В= 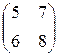 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 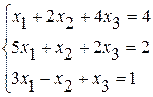
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,1); В (-3,2); С (-1,-4).
Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: 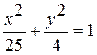 .
.
Задание №5 Составить уравнение конуса, вершина которого находится в точке М(1,-2,7), а направляющая задана уравнениями х2 = 1 – у2 + z2, z = у – х.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
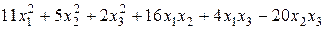 .
.
Задание № 7 Вычислить пределы: 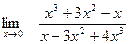 ;
; 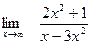
Задание № 8 Найти производные функций:
1. 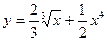 2.
2. 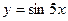
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 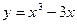 в точке
в точке 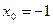 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
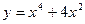
ВАРИАНТ №5
Задание №1 Найти матрицу С, если: С=2АТВ-ВАТ, А= 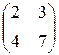 , В=
, В= 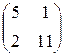 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 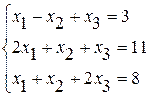
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,3); В (-2,2); С (-3,-5).
Задание №4 Определить фокусы, эксцентриситет, полуоси эллипса: 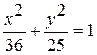 .
.
Задание №5 Составить уравнение поверхности, образованной вращением кривой z = x2, y = 0 вокруг оси Oz.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
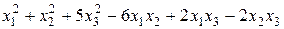 .
.
Задание № 7 Вычислить пределы: 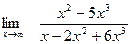 ;
; 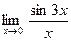
Задание № 8 Найти производные функций:
1. 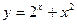 2.
2. 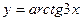
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 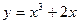 в точке
в точке 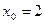 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
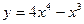
ВАРИАНТ №6
Задание №1 Найти матрицу С, если: С=(В+АВ)Т , А= 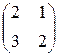 , В=
, В=  .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 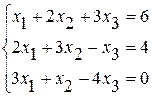
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,1); В (-3,1); С (2,-3).
Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 48; е = 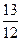 .
.
Задание №5 Составить уравнение поверхности, образованной вращением кривой z = x2 , y = 0 вокруг оси Ox.
Задание № 6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
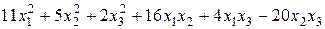
Задание № 7 Вычислить пределы:  ;
; 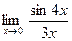
Задание № 8 Найти производные функций:
1. 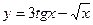 2.
2. 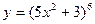
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 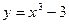 в точке
в точке 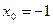 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
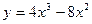
ВАРИАНТ №7
Задание №1 Найти матрицу С, если: С=(А-ВА)Т, А= 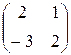 , В=
, В= 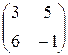 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 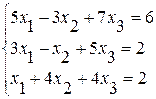
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,2); В (-1,3); С (0,-5).
Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 36; е = 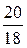 .
.
Задание №5 Составить уравнение поверхности, образованной вращением прямой z = у , х = 0 вокруг оси Oу.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
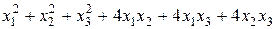 .
.
Задание № 7 Вычислить пределы: 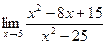 ;
; 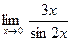
Задание № 8 Найти производные функций:
1. 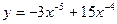 2.
2. 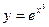
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 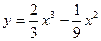 в точке
в точке 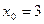 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
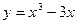
ВАРИАНТ №8
Задание №1 Найти матрицу С, если: С=(АВ+ВА)Т , А= 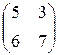 , В=
, В= 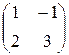 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 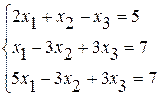
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,2); В (-2,1); С (-5,-5).
Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 32; е = 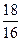 .
.
Задание №5 Составить уравнение поверхности, образованной вращением вокруг оси Oz кривой z = 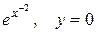 .
.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
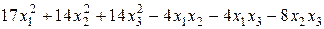 .
.
Задание № 7 Вычислить пределы: 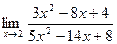 ;
; 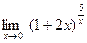
Задание № 8 Найти производные функций:
1. 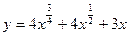 2.
2. 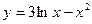
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 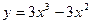 в точке
в точке 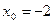 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
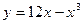
ВАРИАНТ №9
Задание №1 Найти матрицу С, если: С=2А(А-В)Т , А= 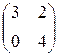 , В=
, В= 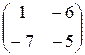 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 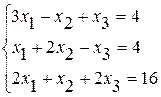
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,3); В (-1,2); С (-4,-4).
Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: а = 42; е = 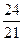 .
.
Задание №5 Составить уравнение поверхности, образованной вращением вокруг оси Oz кривой 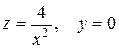 .
.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
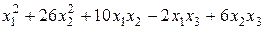 .
.
Задание № 7 Вычислить пределы: 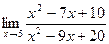 ;
; 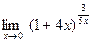
Задание № 8 Найти производные функций:
1. 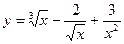 2.
2. 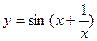
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 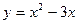 в точке
в точке 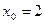 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
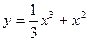
ВАРИАНТ №10
Задание №1 Найти матрицу С, если: С=АТ (В+А), А= 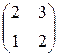 , В=
, В= 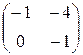 .
.
Задание №2 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера , 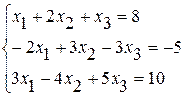
· методом обратной матрицы.
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,3); В (-1,1); С (0,-7).
Задание №4 Составить каноническое уравнение гиперболы, если действительная полуось равна а, эксцентриситет равен е: 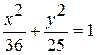
Задание №5 Исследовать форму кривой Г, заданной уравнениями 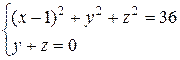 . Определить вид ее проекции на плоскость Оху.
. Определить вид ее проекции на плоскость Оху.
Задание №6 Методом Лагранжа найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду для квадратичной формы.
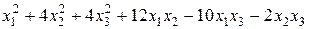 .
.
Задание № 7 Вычислить пределы: 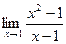 ;
; 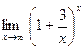
Задание № 8 Найти производные функций:
1. 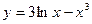 2.
2. 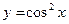
Задание № 9 Решить задачу: Найти уравнение касательной, проведенной к графику функции 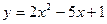 в точке
в точке 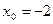 .
. 
Задание № 10 Исследовать функцию с помощью производных и построить график:
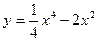
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Абрамов, А.А. Введение в тензорный анализ и риманову геометрию: учеб. пособие для вузов / А.А.Абрамов. - 2-е изд. - М.: Физматлит, 2004. - 111с.
2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006. - 432 с.
3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. - 22-е изд., перераб. - СПб.: Профессия, 2005. - 432 с.
4. Бутузов, В.Ф. Линейная алгебра в вопросах и задачах : учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, А.А.Шишкин; Ред.Бутузов В.Ф. - 2-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 247 с.
5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. - 4-е изд., стереотип. - М.: Дрофа, 2004. - 725 с.
6. Икрамов, Х.Д. Задачник по линейной алгебре: учеб. пособие / Х.Д.Икрамов; ред. В.В.Воеводин. - 2-е изд., испр. - СПб.; М.; Краснодар: Лань, 2006. - 319 с.
7. Ильин, В.А. Линейная алгебра: учеб. пособие / В.А.Ильин, Э.Г.Позняк. - 6-е изд., стереотип. - М.: Физматлит, 2005. - 278 с.
8. Клетеник, Д.В. Сборник задач по аналитической геометрии: учеб. пособие для втузов / Д.В.Клетеник; ред. Н.В.Ефимов. - 17-е изд., стер. - СПб.: Профессия, 2005. - 199 с. - (Специалист).
9. Лукьянов, А.В. Элементы линейной алгебры: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. - Челябинск: Полиграф-Мастер, 2005. - 97с.
10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . - 5-е изд., испр. - М.: ФИЗМАТЛИТ, 2002. - 479 с.
11. Фаддеев, Д.К. Вычислительные методы линейной алгебры / Д.К.Фаддеев, В.Н.Фаддеева . - 3-е изд., стереотип. - СПб.: Лань, 2002. - 733 с.
12. Фаддеев, Д.К. Лекции по алгебре : учеб. пособие для вузов / Д.К.Фаддеев. - 2-е изд., стер. - СПб.: Лань, 2002. - 416 с.
13. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 1 / Г.М. Фихтенгольц. - 6-е изд., стер. - СПб. Лань, 2005. - 440 с. - Алф. указ.: С. 434-440.
14. Фихтенгольц, Г.М. Основы математического анализа: учебник для вузов. Ч. 2 / Г.М.Фихтенгольц. - 6-е изд., стер. - СПб.: Лань, 2005. - 463 с.
15. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 1 / Г. М. Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 440 с.
16. Фихтенгольц, Г.М. Основы математического анализа: учебник. Ч. 2 / Г. М.Фихтенгольц. - 8-е изд. стер. - СПб.; М.; Краснодар: Лань, 2006. - 463 с.
17. Шипачев, В.С. Математический анализ: учеб. пособие для вузов / В.С.Шипачев. - М.: Высш. шк., 2002. - 176 с.
Дополнительная литература:
1. Бубнов, В.А. Линейная алгебра. Компьютерный практикум / В.А. Бубнов, Г.С.Толстова, О.Е.Клемешева. - М.: БИНОМ. Лаборатория Базовых Знаний, 2002. - 99 с.
2. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е.Данко [и др.]. - 6-е изд. - М.: ОНИКС; М.: Мир и Образование, 2007. - 304 с.
3. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: ОНИКС; М. : Мир и Образование, 2008. - 368 с.
4. Ермаков, В.И. Сборник задач по высшей математике для экономистов / В.И. Ермаков. – М.:ИНФРА,2002.
5. Чижов, Е.Б. Введение в философию математических пространств / Е.Б.Чижов. – М.: Едиториал УРРС, 2004
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 4
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ.. 5
ЗАДАНИЯ ДЛЯ ДОМАШНИХ КОНТРОЛЬНЫХ РАБОТ. 21
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ.. 31
ВВЕДЕНИЕ
Целью преподавания дисциплины «математика» состоит в ознакомлении студентов данного направления с основными понятиями, положениями и методами математики. Дисциплина «Высшая математика» формирует базовые знания и кругозор, необходимые для освоения обще-профессиональных и специальных дисциплин. Данный курс способствует созданию условий для формирования профессиональных навыков будущего специалиста.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Раздел 1 Элементы линейной и векторной алгебры
Дата: 2018-12-21, просмотров: 382.