ImageSize (x1,y1,x2,y2) – функция возвращает размер памяти в байтах, необходимый для размещения прямоугольного фрагмента изображения. Здесь (x1,y1) – координаты левого верхнего, (x2,y2) – правого нижнего углов фрагмента изображения.
GetImage(x1,y1,х2,y2,Buf) – процедура помещает в память копию прямоугольного фрагмента изображения. Здесь (x1,y1) – координаты левого верхнего, (x2,y2) – правого нижнего углов фрагмента изображения; Buf — переменная или участок кучи, куда будет помещена копия видеопамяти с фрагментом изображения. Размер Buf должен быть получен с помощью функции ImageSize (x1,y1,x2,y2).
PutImage(x,y,Buf,Mode) – процедура выводит в заданное место экрана копию фрагмента изображения, ранее помещенную в память процедурой GetImage. Здесь (x,y) – координаты левого верхнего угла того места на экране, куда будет скопирован фрагмент изображения; Buf – переменная или участок кучи, откуда берется изображение; Mode – способ копирования. Параметр Mode определяет способ взаимодействия вновь размещаемой копии с уже имеющимся на экране изображением. Взаимодействие осуществляется путем применения кодируемых этим параметром логических операций к каждому биту копии и изображения. Для указания применяемой логической операции можно использовать одну из следующих предварительно определенных констант:
Const
NormalPut=0; {Замена существующего изображения на копию}
XorPut=1; {Исключительное ИЛИ}
OrPut=2; {Объединительное ИЛИ}
AndPut=3; {Логическое И}
NotPut=4; {Инверсия изображения}
Наиболее часто используются операции NormalPut, XorPut и NotPut. Первая из них просто стирает часть экрана и на это место помещает копию из памяти в том виде, как она там сохраняется. Операция NotPut делает то же самое, но копия выводится в инверсном виде. Для монохромного режима это означает замену светящихся пиксел на темные и наоборот. В цветном режиме операция NotPut применяется к коду цвета каждого пиксела. Например, для White (код 15 или в двоичном виде 1111) эта операция даст код 0000=0=Black, для Red – 4=0100 получим 1011=11=LightCyan и т.д. Операция XorPut, примененная к тому же месту экрана, откуда была получена копия, сотрет эту часть экрана. Если эту операцию применить дважды к одному и тому же участку, вид изображения на экране не изменится. Таким способом можно перемещать изображения по экрану, создавая иллюзию движения.
Способы создания движущихся изображений
1 - ый способ. Дважды рисуя одно и то же изображение: первый раз цветом, отличным от цвета фона, второй раз – цветом фона.
2-ой способ. Используя процедуры и функции работы с видеопамятью. Изображение движется с помощью операции NormalPut.
3-ий способ. Используя процедуры и функции работы с видеопамятью. Изображение движется с помощью операции XorPut.
Пример программы движения шарика, падающего с левого верхнего угла экрана по диагонали в правый нижний.
1- ый способ .
Program Demo_1;
Uses
Graph,Crt;
Var
Driver,Mode,i:Integer;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
SetBkColor(Black);
For i:=25 to 300 do {схема движения шарика}
Begin
{рисуем шарик}
SetColor(Red); {цвет границы – красный}
Circle(i,i,15); {рисуем контур шарика}
SetFillStyle(SolidFill,Blue);
{стиль заполнения – синий фон}
FloodFill(i,i,Red); {закрасили}
{стираем шарик, закрашивая его цветом фона}
SetFillStyle(SolidFill,Black);
{стиль заполнения – черный фон}
FloodFill(i,i,Red); {закрасили}
SetColor(Black); {цвет границы – черный}
Circle(i,i,15); {нарисовали черный контур
на черном фоне, шарик исчез}
Delay(3000); {пауза}
end;
{чтобы шарик остался на экране, нарисуем его еще раз}
SetColor(Red);
Circle(i,i,15);
SetFillStyle(SolidFill,Blue);
FloodFill(i,i,Red);
ReadLn;
CloseGraph;
End.
Ой способ .
Program Demo_2;
Uses Graph,Crt;
Var
P :Pointer; {определяем нетипизированный указатель}
Size :Word;
Driver,Mode,i:Integer;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
{рисуем закрашенный шарик}
SetBkColor(Black);
SetColor(Red);
Circle(30,30,15);
SetFillStyle(SolidFill,Blue);
FloodFill(30,30,Red);
size:=ImageSize(5,5,50,50); {определяет объем памяти,}
{необходимый для сохранения изображения}
GetMem(P,Size); {выделяет память в динамически}
{распределяемой области размером в size байт}
GetImage(5,5,50,50,P^); {запоминаем изображение}
for i:=5 to 300 do
Begin
PutImage(i,i,P^,NormalPut); {выводим изображение}
Delay(3000); {пауза}
end;
ReadLn;
CloseGraph;
End.
Ий способ .
Program Demo_3;
Uses Graph,Crt;
Var
P :Pointer; {определяем нетипизированный указатель}
Size :Word;
Driver,Mode,i:Integer;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
{рисуем закрашенный шарик}
SetBkColor(Black);
SetColor(Red);
Circle(30,30,15);
SetFillStyle(SolidFill,Blue);
FloodFill(30,30,Red);
size:=ImageSize(5,5,50,50); {определяет объем памяти,}
{необходимый для сохранения изображения}
GetMem(P,Size); {выделяет память в динамически}
{распределяемой области размером в size байт}
GetImage(5,5,50,50,P^); {запоминаем изображение}
PutImage(i,i,P^,XorPut); {стираем изображение}
for i:=5 to 300 do
Begin
PutImage(i,i,P^, XorPut); {выводим изображение}
Delay(3000); {пауза}
PutImage(i,i,P^,XorPut); {стираем изображение}
end;
ReadLn;
CloseGraph;
End.
Примеры программ работы с графикой
1. Построение мозаичных изображений.
Мозаичное изображение можно построить с помощью рисования прямоугольников. Для задания изображения нужно сформировать матрицу, содержащую вид этого изображения. Каждый элемент матрицы с координатами (i,j) – номер цвета, которым нужно закрасить прямоугольник, находящийся на пересечении i-ой строки и j-го столбца.
Пример. Создать мозаичное изображение вида:
Program Demo_1;
Uses Crt,Graph;
Const
h=10; {высота прямоугольника}
B: array[1..5,1..5] of 0..2=
((0,0,1,0,0), {задаем матрицу размером 5x5}
(0,1,0,1,0), {тип 0..2 – количество используемых цветов}
(1,0,2,0,1),
(0,1,0,1,0),
(0,0,1,0,0));
Var
Driver,Mode,i,j,x,y:Integer;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
For i:=1 to 5 do
Begin
y:=i*h;
for j:=1 to 5 do
Begin
x:=75+j*h;
case B[i,j] of
0:SetFillStyle(1,White); {меняем цвет заполнения}
1:SetFillStyle(1,Blue); {в зависимости от значения}
2:SetFillStyle(1,Yellow) {элемента матрицы}
end;
Bar(x,y,x+h,y+h); {рисуем прямоугольник}
end;
end;
ReadLn;
CloseGraph;
End.
2. Построение графика функции.
Для построения графика функции прежде всего нужно построить систему координат, так как для графического режима она отличается от привычной для пользователя (ось oy направлена сверху вниз, начало координат находится в левом верхнем углу экрана).
| Система координат графического экрана | Декартова система координат |
Для преобразования координат точки (x , y) декартовой системы координат в координаты точки (X , Y) системы координат графического режима можно использовать преобразования:
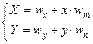
где wm , wn – масштабные коэффициенты по осям, (wx , wn) – координаты центра начала декартовой системы координат на графическом экране.
Пример: построить график функции y=sin(x).
Program Demo_2;
Uses Graph;
Const
a=-10; {[a,c] – отрезок, на котором строится график функции}
c=10;
wm=50; {масштабный множитель по оси ox}
wn=50; {масштабный множитель по оси oy}
Var
Driver,Mode:Integer;
i,wx,wy :Integer;
x,y:Real;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
{Задаем координаты начала системы координат в центре экрана}
wx:=GetMaxX div 2;
wy:=GetMaxY div 2;
{Рисуем оси}
SetColor(Red);
SetLineStyle (SolidLn,0,ThickWidth);
Line(0,wy,GetMaxX,wy); {ox}
Line(wx,0,wx,GetMaxY); {oy}
{Подписи осей}
SetColor(White);
OutTextXY(wx+7,4,'Y');
OutTextXY(GetMaxX-8,wy+6,'X');
{Вертикальные линии сетки}
SetColor(Green);
SetLineStyle (SolidLn,0,NormWidth);
i:=1;
While (wx-i*wm>0) or (wx+i*wm<GetMaxX) do
Begin
Line(wx-i*wm,0,wx-i*wm,GetMaxY);
Line(wx+i*wm,0,wx+i*wm,GetMaxY);
Inc(i);
end;
{Горизонтальные линии сетки}
i:=1;
While (wy-i*wn>0) or (wy+i*wn<GetMaxY) do
Begin
Line(0,wy-i*wn,GetMaxX,wy-i*wn);
Line(0,wy+i*wn,GetMaxX,wy+i*wn);
Inc(i);
end;
{Строим график точками}
i:=a*wm;
While i<=c*wm do
Begin
x:=i/wm;
y:=sin(x);
PutPixel(Round(wx+wm*x),Round(wy+wn*y),White);
i:=i+1;
end;
ReadLn;
CloseGraph;
End.
3. Построение круговых и столбчатых диаграмм.
Построить круговую и столбчатую диаграммы, содержащие сведения о знаменитых алмазах следующего вида:
Для построения диаграмм нужно определить 2 массива: первый содержит значения массы в каратах (массив А[1..5]), второй – названия алмазов (массив Y[1..5]).
Расчет высоты столбика производится следующим образом:
· находим самый большой алмаз (max). Пусть этому значению соответствует столбик в 200 пиксел;
· высота каждого столбика равна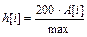 
.
Градусная мера угла для построения круговых диаграмм рассчитывается так:
· находим сумму в каратах всех знаменитых алмазов (sum). Этому значению будет соответствует угол в 3600;
· градусную меру каждого угла определим из формулы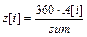 
.
Program Demo_3;
Uses Graph,Crt;
Type
Mas1=array[1..5] of Real;
Mas2=array[1..5] of String[15];
Const
N=5; {количество данных}
A:Mas1=(3106,971,968,787,770); {значения}
Y:Mas2=('Куллинан','Эльсценсиор',
'Сьерра-Леоне','Великий Могол',
'Река Уойе'); {подписи данных}
Var
Driver,Mode :Integer;
Z :array[1..N] of Integer;
T :String[15];
max,sum :Real;
y0,y1,y2,h,pr,x,rx,osn,
ras,I :Integer;
{Круговая диаграмма}
Procedure Sect;
Begin
OutTextXY(100,30,
'Знаменитые алмазы (масса в каратах)');
{расчет общей суммы}
sum:=0;
For i:=1 to N do
sum:=sum+A[i];
For i:=1 to N do
Z[i]:=Round(a[i]*360/sum);
y0:=0;
{рисование сектора}
For i:=1 to N do
Begin
SetFillStyle(2,i+1);
PiesLice(325,190,y0,y0+z[i],140);
y0:=y0+z[i];
end;
y1:=50;
y2:=70;
{рисование легенды и подписи к ней}
For i:=1 to N do
Begin
SetFillStyle(2,i+1);
Bar3d(20,y1,60,y2,5,True);
Str(A[i]:6:1,t);
OutTextXY(70,y1+10,t);
y1:=y1+30;
y2:=y2+30;
end;
ReadLn;
End;
{Столбчатая диаграмма}
Procedure Stol;
Begin
ClearDevice;
x:=50;
rx:=30; {ширина столбика}
ras:=Round(500/N); {расстояние между столбиками}
osn:=250; {координата основания}
Rectangle(x,osn,500, osn+35);
SetTextStyle(4,0,2);
pr:=0;
OutTextXY(100,30,
'Знаменитые алмазы (масса в каратах)');
max:=A[1];
For i:=1 to N do
If A[i]>max then max:=A[i];
For i:=1 to N do
Begin
OutTextXY(x+10,osn+5,Y[i]);
h:=Trunc(A[i]*200/max); {высота}
SetFillStyle(9,i+10);
Bar (x, 250-h,x+rx, osn);
Str(a[i]:6:1,t);
OutTextXY(x,250-h-12,t);
x:=x+ras;
end;
ReadLn;
end;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
Stol;
Sect;
CloseGraph;
End.
4. Построение вероятностных изображений.
Рассмотрим пример построения листа папоротника. Заданное множество точек строится с помощью четырех преобразовании координат точек плоскости, каждое из которых применяется с определенной вероятностью. Преобразования задаются матрицей коэффициентов и вектором смещения вдоль оси y:
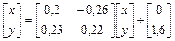, вероятность рÎ(0,85;0,92];
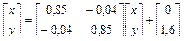, вероятность рÎ[0;0,85];
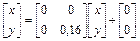, вероятность рÎ(0,99;1];
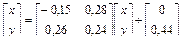, вероятность рÎ(0,92;0,99].
Program Paporotnik;
Uses Graph,Crt;
Const
iteration=500000;
Var
t,x,y,p :Real;
k :LongInt;
Driver,Mode,mid_x,mid_y,r :Integer;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
mid_x:=GetMaxX div 2;
mid_y:=GetMaxY;
r:=Trunc(0.1*mid_y);
Randomize;
x:=1.0;
y:=0.0;
For k:=1 to iteration do
Begin
p:=Random;
t:=x;
If p<=0.85 then
Begin
x:=0.85*x+0.04*y;
y:=-0.04*t+0.85*y+1.6;
End
Else
If p<=0.92 then
Begin
x:=0.2*x-0.26*y;
y:=0.23*t+0.22*y+1.6;
End
Else
If p<=0.99 then
begin
x:=-0.15*x+0.28*y;
y:=0.26*t+0.24*y+0.44;
end
else
begin
x:=0.0;
y:=0.16*y;
end;
PutPixel(mid_x+Round(r*x),
mid_y-Round(r*y),LightGreen);
end;
ReadLn;
CloseGraph;
End.
5. Построение фрактальных изображений.
Фрактал – это самоподобный объект, у которого любая меньшая часть похожа на целый объект. Обычно фрактальные фигуры строятся с помощью рекурсивных подпрограмм. Простейшим примером фрактальной фигуры является снежинка:
Алгоритм рисования снежинки: из одной точки – центра вырастают k кристалликов-отрезков длины r, свободный конец каждого из которых служит центром новой снежинки с длиной кристаллика–отрезка, в 3 раза меньшей r. Указанный процесс продолжается n раз. Выше показаны снежинки при n=1,2 и k=6.
Для построения снежинок введем рекурсивную процедуру, параметрами которой будут координаты центра снежинок x0, y0, радиус– длина r и глубина рекурсии n. Для размещения рисунка в центре экран начальный радиус определим по формуле: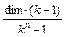 
, полагая dim=240, k=1/3. Получим: k=160/(1–1/3n). Координаты концов отрезка (x , y) будем находить, используя параметрическое задание уравнения окружности со смещением на заданный угол:
.
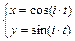Чтобы величины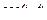 
и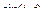 
не вычислялись в цикле многократно, запомним их значения в массивах C и S.
Program Sneg;
Uses Graph;
Const
k=6; {количество кристаллов}
n=5; {глубина рекурсии}
t=2*Pi/k; {угол поворота}
Var
Driver,Mode,I :Integer;
C,S :array[1..k] of Real;
Procedure Snow(x0,y0,r,m:Integer);
Var
x,y,i:Integer;
Begin
For i:=1 to k do
Begin
x:=x0+Round(r*C[i]);
y:=y0-Round(r*S[i]);
Line(x0,y0,x,y);
If m>1 then Snow(x,y,r div 3,m-1)
end;
End;
Begin
Driver:=Detect;
InitGraph(Driver,Mode,'');
For i:=1 to k do
Begin
C[i]:=Cos(i*t);
S[i]:=Sin(i*t);
end;
Snow(GetMaxX div 2,GetMaxY div 2,
Round(160/(1-1/(Exp(n*Ln(3))))),n);
ReadLn;
CloseGraph;
End.
ЛИТЕРАТУРА
1. Бородич Ю.С. и др. Паскаль для персональных компьютеров: Справ. Пособие / Ю.С.Бородич, А.Н.Вальвачев, А.И.Кузьмич. – Мн.: Выш. шк.: БФ ГИТМП «НИКА», 1991. – 365 с.
2. Вальвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для персональных ЭВМ ЕС: Справ. пособие. – Мн.: Выш.шк., 1989. – 223 с.: ил.
3. Офицеров Д.В. и др. Программирование на персональных ЭВМ: Практикум: Учеб. Пособие / Д.В.Офицеров, А.Б. Долгий, В.А.Старых; Под общ. ред. Д.В.Офицерова. – Мн.: Выш.шк., 1993. – 256 с.
4. Немнюгин С.А. Turbo Pascal: практикум – СПб: Питер, 200. – 256 с.:ил.
5. Пантелеева З.Т. Графика вычислительных процессов: Учеб.пособие. – М.: Финансы и статистика, 1983. – 167 с., ил.
6. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: «Нолидж», 1997. – 616 с., ил.
7. Фигурнов В.Э. IBM PC для пользователя. Изд. 7-е, перераб. И доп. – М.: ИНФРА – М, 1997. – 640 с.: ил.
Учебное издание
Ружицкая Елена Адольфовна
Карасёва Галина Леонидовна
Орлов Владимир Васильевич
Смородин Виктор Сергеевич
Дёмова Тамара Максимовна
Богданова Татьяна Григорьевна
Дата: 2018-11-18, просмотров: 434.
