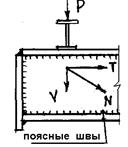
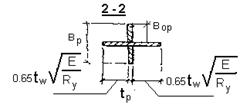
Ближе к середине балки влияние касательных напряжений на стенку невелико. Здесь действуют главным образом нормальные напряжения от изгиба балки. Выпучиваясь, стенка образует в сжатой зоне балки практически вертикальные волны, перпендикулярные ее плоскости. Поперечные ребра не могут оказать существенного влияния на выпучивание стенки, т. к. длина волн выпучивания небольшая (длина полуволны 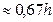 ), а их направление параллельно поперечным ребрам жесткости. Поэтому в очень гибких стенках
), а их направление параллельно поперечным ребрам жесткости. Поэтому в очень гибких стенках 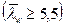 от действия нормальных напряжений в сжатой части стенки ставят продольные ребра жесткости, уменьшающие расчетную ширину пластинки и увеличивающие критические напряжения.
от действия нормальных напряжений в сжатой части стенки ставят продольные ребра жесткости, уменьшающие расчетную ширину пластинки и увеличивающие критические напряжения.
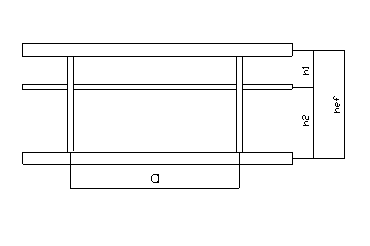
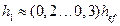
Наличие продольного ребра улучшает устойчивость стенки, т. к. разбивает стенку по высоте на 2отсека, устойчивость которых проверяется отдельно.
Расчет на устойчивость отсека стенки между ребрами жесткости и поясами на действие средних (в пределах отсека) нормальных и касательных напряжений 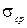 и
и 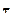 , а также местных напряжений
, а также местных напряжений 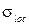 .
.
Сжимающие напряжения 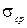 у сжатой границы стенки и средние касательные напряжения вычисляются по формулам:
у сжатой границы стенки и средние касательные напряжения вычисляются по формулам:
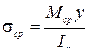 ; для симметричного сечения
; для симметричного сечения 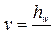 ;
; 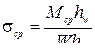 ,
,
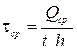
где 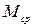 и
и 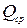 – средние значения момента и поперечной силы в пределах отсека. Если длина отсека «а» превышает его высоту, то осреднение выполняется в пределах наиболее нагруженного участка отсека «а´» с длиной, равной
– средние значения момента и поперечной силы в пределах отсека. Если длина отсека «а» превышает его высоту, то осреднение выполняется в пределах наиболее нагруженного участка отсека «а´» с длиной, равной 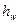 . Величина местных напряжений в стенке
. Величина местных напряжений в стенке 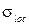 определяется по формуле
определяется по формуле 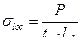
Устойчивость стенок балок 1-го класса (упругая работа) симметричного сечения, укрепленных только поперечными ребрами жесткости, при условной гибкости стенки 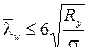 и
и  считают обеспеченной, если выполнено условие:
считают обеспеченной, если выполнено условие:
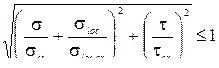 )
)
В приведенной формуле обозначено:
А) 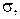
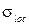 ,
, 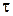 – средние и локальные напряжения, определяемые по вышеприведенным формулам от внешних нагрузок
– средние и локальные напряжения, определяемые по вышеприведенным формулам от внешних нагрузок
Б) 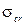 – критическое напряжение, вычисляемое по формуле:
– критическое напряжение, вычисляемое по формуле: 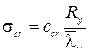 ,
,
где 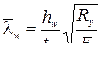 ;
;
 – коэффициент, определяемый по таблицам для двух случаев:
– коэффициент, определяемый по таблицам для двух случаев:
а) при отношении 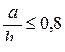 (короткий отсек)
(короткий отсек)
б) при отношении 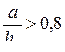 (длинный отсек),
(длинный отсек),
здесь 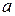 – расстояние между осями поперечных ребер жесткости.
– расстояние между осями поперечных ребер жесткости.
В) Локальное критическое напряжение  :
:
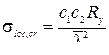 ,
,
где с1 с2 – коэффициенты, принимаемые по таблицам в зависимости от отношения 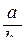 и значения
и значения 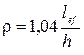 , здесь
, здесь 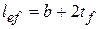 (b – ширина полки балки настила).
(b – ширина полки балки настила).
Г) Касательное критическое напряжение  :
:
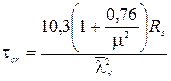 ,
,
где 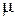 – отношение большей стороны отсека стенки к меньшей;
– отношение большей стороны отсека стенки к меньшей;
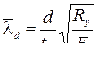 ,
,
где d – меньшая из сторон отсека (  или a).
или a).
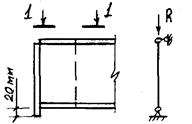
Расчет поясных швов.
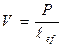 - давление от сосредоточенной нагрузки на единицу длины-1см.
- давление от сосредоточенной нагрузки на единицу длины-1см.
|
|
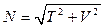 ,
, 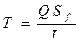 ,
,
где 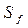 – статический момент пояса относительно нейтральной оси.
– статический момент пояса относительно нейтральной оси.
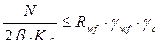 - по металлу шва.
- по металлу шва.
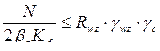 - по металлу границы сплавления.
- по металлу границы сплавления.
Откуда 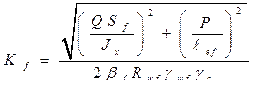 – по металлу шва,
– по металлу шва,
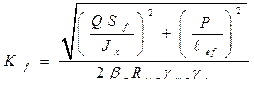 – по металлу границы сплавления.
– по металлу границы сплавления.
Расчет опорного ребра
|
|
Требуемая площадь опорного ребра из условия сжатия 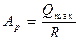 .
.
|
|
Ширина опорного ребра, 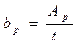 но не менее 180
но не менее 180 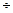 200мм,
200мм,  мм. – толщина опорного ребра.
мм. – толщина опорного ребра.
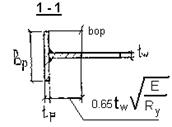
Ширина выступающей части ребра из условия его местной устойчивости не должна превышать
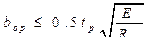 .
.
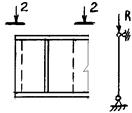
Проверка устойчивости опорной части балки из плоскости балки как стойки, нагруженной опорной реакцией R:
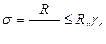 ,
,
где 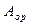 – площадь заштрихованной части,
– площадь заштрихованной части, 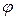 – коэффициент продольного изгиба при сжатии.
– коэффициент продольного изгиба при сжатии.
Требуемый катет швов, прикрепляющих опорное ребро к стенке балки.
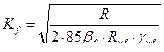 .
.
Дата: 2018-11-18, просмотров: 801.