операции логического умножения – конъюнкции ( 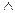 ),
),
логического сложения – дизъюнкции ( 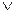 ),
),
исключающего или – ( Å ),
логического отрицания – инверсии ( 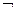 ).
).
Таблицы истинности для указанных операций:
| A | B | A V B | A L B | A Å B |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
4. Стрелка Пирса X ¯ Y.
Стрелка Пирса X ¯ Y (NOR (NOT OR), ИЛИ-НЕ) – это высказывание, которое истинно только в том случае, если X ложно и Y ложно.
5. Штрих Шеффера X | Y.
Штрих Шеффера X | Y (NAND (NOT AND), И-НЕ) – это высказывание, которое ложно только в том случае, если X истинно и Y истинно.
Определить значения логических операций при различных сочетаниях аргументов можно из таблицы истинности.
Таблица истинности для основных логических операций, используемых в ЭВМ
| X | Y | 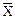
| XY | X + Y | X ¯ Y | X | Y |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Пример x в [a,b]
| Закон тождества | Всякое высказывание тождественно самому себе. | |
| Закон непротиворечия | Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно. | А & A = 0 |
| Закон исключенного третьего | Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина». | А \/ A = 1 |
| Закон двойного отрицания | Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание. | ( A) = A |
| Законы де Моргана | ( А & B) = А \/ B ( А \/ B) = А & B | |
|
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в алгебре.
| ||
| Закон коммутативности (переместительный) | В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения. | А & В = В & А А \/ В = А \/ В |
| Закон ассоциативности (сочетательный) | Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять. | (А & B) & С = А & (В & С) (А \/ В) \/ С= А \/ (В \/ С) |
| Закон дистрибутивности (распределительный ) | В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые. | (А&В) \/ (А&С) = А&(В\/С) (А\/В) & (А\/С) = А \/ (В&С) |
Классификация ЭВМ
Компьютер – это электронное устройство для автоматизации процессов создания, хранения, воспроизведения, обработки и транспортировки данных.
Дата: 2018-11-18, просмотров: 686.