Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

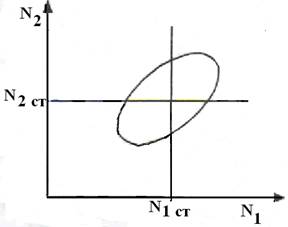
Рис2. Графическая зависимость изменения численности популяций. Фазовый портрет системы.

 

 

Однако и здесь имеют место следующие закономерности:

Вывод 3:

Колебания численности популяций, N ₁ и N ₂ , действительно имеют место, они сдвинуты по фазе, но не являются гармоническими.

В экосистеме возникает то, что называется биоритмом.

 

 

В заключении приведем график, построенный на основании отчетов по отстрелу зайцев и рысей в Канаде в течении столетия. Видно, что основные выводы, полученные в упрощенной схеме «хищник-жертва», справедливы и для этой реальной ситуации.

 

 

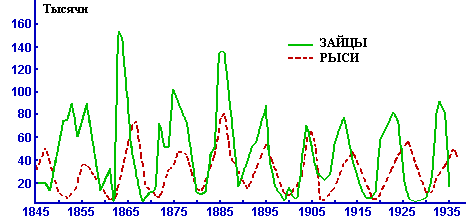
Рис3. Соотношение популяций рысей и зайцев по результатам отчетов канадской меховой компании

 

Фармакокинетическая модель.

 

Рассмотрим модель, описывающую кинематику распределения вве­денных в организм препаратов (лекарств). Будем считать, что терапевти­ческий эффект зависит от концентрации препарата в больном органе (органе-мишени) и времени нахождения лекарства в действующей концентрации. Модель должна дать ответ о дозе лекарства, пути и периодичности введения, которое обеспечивало бы достаточный терапевтический эффект при минимальном побочном действии.

Из физиологии известно, что концентрация препарата в органе может зависеть от ряда процессов, скорости которых характеризуются константами К:

1). Всасывание препарата в кровяное русло при внесосудистом введении - константа – К₁₂.

Рис.4. Схематичное изображение фармакокинетической модели

 

2). Транспорт препарата из крови в органы – К₂₃.

3). Транспорт препарата из органа в кровь - К₃₂.

4). Удаление (элиминация) препарата из крови почками и разруше­ние его печенью – К₄.

Всякая модель предполагает упрощение реальных процессов. В этой модели рассматривается только кинетика, т.е. течение во времени всех процессов без выяснения их причин. Организм представляется в виде отдельных простых блоков (кровь, орган-мишень, органы, элиминирующие препарат) - фармакокинетических камер, т.е. частей системы, в пределах каждой из которых распределение препарата предполагается равномерным. Есть еще целый ряд упрощений. Например, не учитывается периодичность в чувствительности и функционировании органов, влияние препарата на органы и т.д. Но все это позволяет описывать изменение концентрации препарата в блоках простыми линейными дифференциальными уравнениями.

Например, небольшое изменение (убыль) концентрации препарата 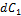 в первом блоке после введения за время :    

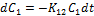
Заметим, что каким бы сложным ни был процесс, всегда можно вы­делить такой малый промежуток времени, в течение которого процесс будет линейным.

Учитывая поступление и введение препарата в блоках, для скоростей изменения концентраций получим систему уравнений

 

 

 

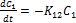
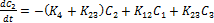
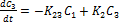
Всегда решаются, т.е. интегрируются, только дифференциальные уравнения первой степени, к которым и стараются свести путем преобразований и упрощений системы из нескольких уравнений.

Один из способов упрощения системы - объединение нескольких блоков в один или удаление несущественных элементов

Другой способ – рассматривать часть системы как стационарную, тогда в этой части системы 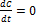 и дифференциальное уравнение превращается в алгебраическое.

Рассмотрим более простую систему. Предположим, что необходимо создать и некоторое время поддерживать постоянную концентрацию некоторого препарата в крови (например, рентгеноконтрастного вещества, введение которого в кровоток дает возможность делать компьютерные рентгеновские томограммы). Допустим, что препарат непрерывно со скоростью Q поступает в кровь , и тогда изменение его количества в крови

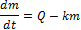
где К– константа удаления препарата из крови. Предположим, что в момент t =0, масса препарата в крови =0. Тогда можно проинтегрировать дифференциальное уравнение, предварительно разделив переменные, и найти его частное решение.

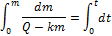
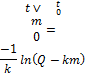
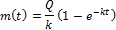
Для получения зависимости C ( t ) разделим обе части уравнения на объем 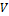, в котором распределяется препарат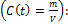

Объём распределения лекарственного вещества --это гипотетический объём жидкостей организма, необходимый для равномерного распределения всего количества данного вещества в концентрации, равной его концентрации в плазме крови. Объём распределения зависит от физико-химических свойств препарата (молекулярная масса, уровень ионизации и полярности, растворимость в воде и жирах), которые влияют на его прохождение через мембраны, возраста, пола больного, общего количества жиров в организме. В клинической практике объём распределения служит для расчета нагрузочной дозы препарата, требуемой для достижения его необходимой концентрации в крови.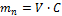

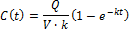
При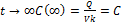  

Рис.5. Зависимость концентрации препарата в крови от времени.

 

Из решения видно, что для достижения в крови некоторой постоянной концентрации препарата 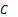 его следует вводить со скоростью:

 

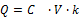
Время достижения уровня С* будет также будет зависеть от константы скорости выведения препарата К. Таким образом, совершенно очевидно, что лечебная концентрация препарата в крови устанавливается не мгновенно, как хотелось бы в лечебных целях, а по прошествии некоторого времени 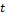. Можно для более быстрого достижения уровня С* сочетать непрерывное введение препарата с начальным разовым введением некоторой нагрузочной дозы .

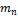Нагрузочная доза препарата в крови будет уменьшаться по закону

,

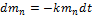из которого следует закон изменения количества препарата со временем.

 

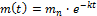
Объединяя оба процесса, получим для изменения концентрации

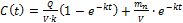 или

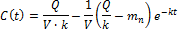
При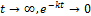

 

 

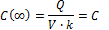
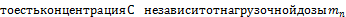
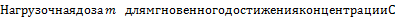
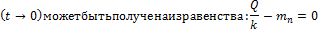
Таким образом, для мгновенного создания в крови желаемой концен­трации 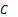 необходимо ввести нагрузочную дозу т* и

вести инфузиюсо скоростью: .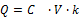

 

 

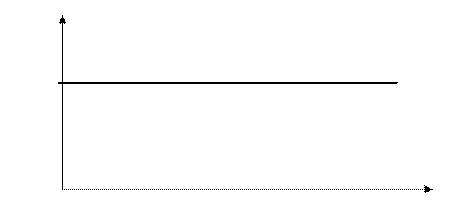Рис 6. Зависимость концентрации препарата в крови от времени при введении нагрузочной дозы.

Этот теоретический вывод был подтвержден экспериментально, что и является решающей проверкой правильности модели.

Более сложные модели можно построить путем суммирования блоков, если мы будем оставаться в рамках линейного приближения, т.е. описывать ситуацию линейными дифференциальными уравнениями.

 

Задача1. Найти закон убывания препарата в организме человека, если через 2 часа после введения 30 мг препарата (инъекция) его масса уменьшилась в четыре раза . Какое количество препарата останется в организме через 3 часа?

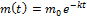
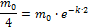
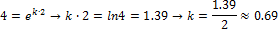
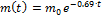
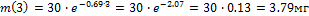
Задача 2. Найти объём распространения препарата в организме V и константу удаления препарата к, если известно, что концентрация препарата в плазме через 2 часа 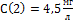, а через 6 часов 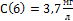. Доза 400мг, введение внутривенное(инъекция).

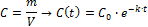
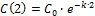
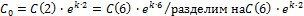
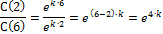
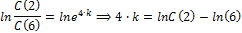
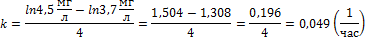
Найдём концентрацию в начальный момент времени:

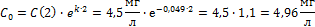
Найдем объём распространения препарата в организме:

 

 

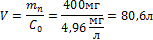
Контрольные вопросы.

Модель «Хищник – жертва».

Стационарные решения.

Основные выводы.

Фармакокинетические модели.

Модель инъекции.

Модель диффузии.

Основные выводы.

Математическое моделирование.

 

Моделирование – это исследование явлений и процессов на моделях. Построение модели связано с упрощением изучаемого процесса, в то же время модель должна отражать основные свойства оригинала.

 

В биологии и медицине используют четыре типа моделей:

      1).Биологические. На них изучают общие биологические закономерности, патологические процессы, методы лечения и т.д. (Эксперименты на лабораторных животных).

      2).Физические, которые ведут себя аналогично оригиналу. (Аппараты искусственного дыхания, кровообращения и т.д.).

      3).Кибернетические – это различные электронные устройства, с помощью которых моделируются информационные процессы в живом организме.( Управление движением руки, ноги, искусственный интеллект и т.д.).

4).Математические. Моделируется математическая зависимость, которая описывает данный процесс. Позволяет

 - уменьшить время исследования и число экспериментов;

 - давать прогноз течения болезни и подобрать оптимальные варианты лечения;

 - судить о таких системах и в таких условиях, которые сложно создать в эксперименте или клинике.

 

При построенииматематической модели различают 3 этапа:

1). Изучение процесса или явления, сбор данных о его параметрах и создание описательной теории, в которой выявляются причинно-следственные связи, существенные и несущественные детали процесса.

2). Составление математических (чаще всего дифференциальныхуравнений).

3). Рассмотрение на модели возможных результатов и выявление наиболее вероятного исхода, т.е. анализ решения уравнений.

При моделировании сложного процесса приходится составлять систему из большого числа дифференциальных уравнений, которые содержат большое число параметров. Для решения уравнений и определения параметров используют ЭВМ.

Основные направления математического моделирования:

1. Модели проницаемости клеточных мембран (нервная проводимость).

2. Иммунология и эндокринология (ход болезни и лечебные мероприятия).

3. Эпидемиология – распространение инфекционных болезней.

4. Процессы транспорта электронов.

5. Моделирование процесса старения клеток, злокачественных образований.

Математическое моделирование биологических процессов началось с создания первых простейших моделей экологической системы.

Попытки математического моделирования динамики, как отдельных биологических популяций, так и сообществ, включающих взаимодействующие популяции различных видов, предпринимались давно. Одна из первых моделей роста изолированной популяции была предложена ещё в 1798 году Томасом Мальтусом:

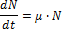
Данная модель задаётся следующими параметрами:

N – численность популяции;

μ – разность между коэффициентами рождаемости и смертности.

 

Модель совместного сосуществования двух биологических видов (популяций) типа «хищник-жертва» впервые была получена американским математиком Альфредом Лоткой в 1925 году. В 1926 году (независимо от Лотки) аналогичные (и более сложные модели) были разработаны итальянским математиком Вито Вольтеррой. Его глубокие исследования в области экологических проблем создали основу математической теории биологических сообществ ( математической экологии).

Поэтому эта классическая математическая модель («хищник-жертва») известна как модель « Лотки-Вольтерра».

 

Модель Лотки-Вольтерра (хищник-жертва).

Допустим, в некотором замкнутом районе живут рыси и зайцы. Рыси питаются только зайцами, а зайцы - растительной пищей, имеющейся в неограниченном количестве. Необходимо найти макроскопические харак­теристики, описывающие популяции. Такими характеристиками являются число особей в популяциях - число зайцев N ₁ и число рысей N ₂.

Запишем дифференциальные уравнения, описывающие процесс из­менения числа особей во времени.

При отсутствии рысей, изменение числа зайцев будет:

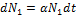
α - коэффициент, характеризующий размножение зайцев (жертв).

При отсутствии зайцев, изменение числа рысей будет:

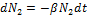
β - коэффициент, характеризующий вымирание рысей (хищников).

При совместном существовании зайцев и рысей:

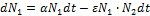
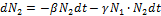
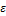 - коэффициент, характеризующий убыль зайцев, вследствие их встреч с рысями.

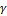 - коэффициент, характеризующий прирост рысей, вследствие их встреч с зайцами.

Скорость изменения популяций

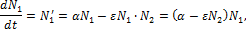
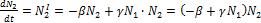                   (1)

Т.е. имеем систему нелинейных дифференциальных уравнений. В стационарном состоянии, когда не изменяется численность зайцев и рысей имеем:

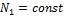 и 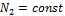 и, следовательно,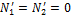

Т.е.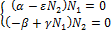

Решение этих уравнений (особые точки):

 

 

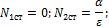
                                                                                                    (2)

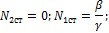
Отсюда следует:

 

Вывод1:стационарные состояния не зависят от численности популяции, а определяются только коэффициентами прироста и потерь для другого вида.

Для определения устойчивости в стационарных состояниях необходимо исследовать систему вблизи этих состояний.

Допустим, возникли некоторые случайные отклонения, флуктуации n ₁ , и n _г . Определим поведение системы.

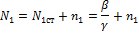
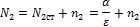
Возьмем производные. С учетом того, что производная от стационар­ного состояния равна 0, получим:

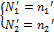
Подставив в (1), раскроем скобки, приведем подобные члены и пренебрежем членам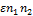и  и 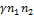 вследствие их предполагаемой малости. Результатом пренеб­режения ими будет линеаризация уравнений. В результате всех преобразований, окончательно получаем систему линейных дифференциальных уравнений второго порядка типа 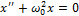, описывающих консервативную колебательную систему, (т.е. идеализированную систему, в которой запас энергии в процессе колебаний остается постоянным):

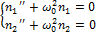
Решив эту систему уравнений получаем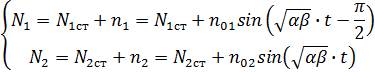

 

 

где: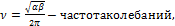

 

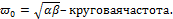
Вывод 2:популяции жертв и хищников испытывают периодические колебания одинаковой частоты , смещенные по фазе (причем максимум численности жертв всегда опережает максимум численности хищников).

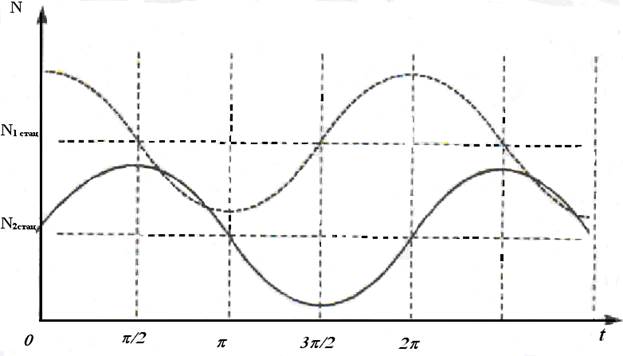
Рис 1.Зависимость изменения популяций от времени.

 

Рассмотрим график зависимости N ₁от N ₂, т.е. избавимся от t.

Очевидно, что упрощенное решение нашей системы дифференциальных уравнений путем избавления от элементов 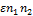 и 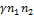 привело нас к тому, что модель пришлось стишком идеализировать, что плохо соответствует реальной модели.

Сделаем попытку решить систему дифференциальных уравнений (1) другим методом. Разделим одно уравнение на другое, тогда получим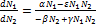  

Разделив переменные и проинтегрировав, получим решение:

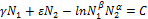
Константу С можно найти в некоторый момент времени, когда мы знаем N ₁ и N ₂ ясно, что она может принимать множество значений.

Итак, мы получили выражение, связывающее две переменные 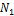 и 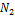, т.е. зависимость 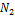= f ( 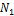)в неявном виде.

Начертим график этой функции. Полученная замкнутая кривая не является эллипсом (рис.2 ), хотя отдаленно и напоминает эллипс, который получается при сложении колебаний одинаковой частоты и произвольной фазы.