В 1970 г. в журнале, издающемся Федеральным банком г. Сент-Луиса, была опубликована статья, в которой излагалась эконометрическая модель, описывающая воздействие кредитно-денежной политики на экономику в духе монетаризма . Эта модель противостояла построенной примерно в то же время совместными усилиями экономистов из Совета управляющих Федеральной резервной системы и Массачусетсского технологического института эконометрической модели FRS-MIT, которая отражала кейнсианское видение механизма воздействия денег на экономику.
Сент-луисская модель представляла систему из восьми приведенных уравнений. Экзогенные переменные модели: масса денег в обращении, правительственные расходы на поддержание занятости, потенциальный уровень производства, прошлые темпы инфляции; эндогенные — изменение совокупных расходов, избыточный спрос, изменения уровня производства, текущий темп инфляции (зависит от величины избыточного спроса), ожидаемые изменения уровня цен (задаются как адаптивные ожидания), расхождения между достигнутым и потенциальным обменом производства, уровень безработицы, процентные ставки (зависят от изменений массы денег, цен и их ожиданий) .
Расчеты проводились в основном на квартальных данных за 1953— 1968 гг. Эта модель показала, что изменения массы денег главным образом влияют на уровень цен, но в краткосрочном периоде также воздействуют на уровень производства. Причем предполагалась следующая последовательность воздействия: изменение массы денег ведет к изменению совокупных расходов, что воздействует на объем производства и через избыточный спрос — на общий уровень цен. В полной мере воздействие массы денег на цены и объем производства проявляется примерно через год после первоначального изменения массы денег.
На основании модели были сделаны следующие выводы:
переменная, отражающая изменение государственных расходов на поддержание занятости, не существенна, а следовательно, фискальная политика сама по себе оказывает лишь временное и незначительное воздействие на уровень экономической активности;
модель устойчива: после изменения одной экзогенной переменной система достаточно быстро возвращалась к траектории устойчивого роста.
Но, несмотря на эти результаты, модель не разрешила споры между противниками и сторонниками монетаризма и даже не стала убедительным подтверждением монетаристских положений. Дело в том, что, хотя структура лагов в уравнении совокупных расходов оказалась достаточно устойчивой, годовой лаг воздействия кредитно-денежной политики на экономику слишком велик, с точки зрения монетаристов, чтобы можно было игнорировать возможность «развертывания» процесса по кейнсианскому сценарию.
Не очень надежными оказались и прогнозы, полученные на базе этой модели. Если при использовании уравнений, построенных на основе данных за 1953—1968 гг., были получены удовлетворительные прогнозы на 1953—1970 гг., то прогнозы на 1973—1975 гг. содержали большие погрешности. Монетаристы попытались объяснить подобную неудачу аномальными изменениями цен, вызванными нефтяным шоком, агрессивной политикой профсоюзов, наконец, ошибками администрации. Но, несмотря на эти объяснения, неудовлетворенность моделью оставалась.
Andersen L., Carlson K. A Monetarist Model for Economic Stabilization // Federal Reserve Bank ofSt.Louis Review. 1970, April.
См. приложение 1.
Модель номинального дохода
Параллельно с эконометрическими исследованиями создавалась и теоретическая основа монетаризма — модель номинального дохода Фридмена .
Эта модель может быть представлена следующим образом:
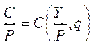 (1)
(1)
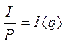 (2)
(2)
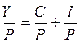 (3)
(3)
q=q* (4)
M=F(r)Y (5)
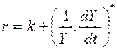 (6)
(6)
k=q*-g*, k- const (7)
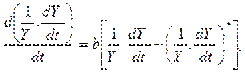 (8)
(8)
где Y— номинальный доход, С — потребление в текущих ценах, I — инвестиции в текущих ценах, Р— индекс цен, q — реальный процент, т.е. процент при отсутствии инфляции, g —темп роста реального дохода (производства), знак * — относится к ожидаемым значениям соответствующей переменной.
Что характерно для этой модели?
В ней можно выделить две независимые части: реальная — уравнения (1) - (4) и денежная - уравнения (5) - (8). Именно вторая и представляет вклад Фридмена.
Уравнение (5) предполагает, что эластичность спроса на деньги по доходу равна 1.
Уравнение (6) получено в результате несложных преобразований из уравнения Фишера, устанавливающего связь между реальным процентом и темпом инфляции: 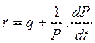 при следующих условиях:
при следующих условиях:
r=r*, q—g=k, k=const. Причем последнее условие означает неизменность распределения доходов, а также содержит предположение о полном использовании ресурсов, в том числе и рабочей силы. Уравнение (8) задает адаптивный характер ожиданий . В этой модели ожидания могут быть заданы и через переменную общего уровня цен. В этом случае вместо уравнения (8) получим следующее уравнение:
 (8-a)
(8-a)
где а — коэффициент адаптации.
Принципиальное значение в модели имеют два механизма: воздействия денег на процент, а через него на ожидаемое изменение номинального дохода (уравнения 5, 6), и адаптации, отражающий способность системы адаптироваться к отклонениям номинального дохода от ожидаемого его уровня (уравнение 8). Оба эти механизма во взаимодействии и определяют траекторию краткосрочного движения. Эта траектория описывается следующим уравнением, полученным путем несложных преобразований из модели:
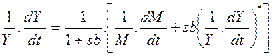 , (9)
, (9)
где s — параметр, отражающий характеристики функции спроса на деньги.
От уравнения (9) легко перейти к уравнению стационарной траектории,описывающей движение в ситуации, когда ожидаемые и действительные значения темпов роста номинального дохода совпадают.
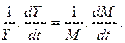 (10)
(10)
Очевидно, что в этом случае темпы роста номинального дохода и денег равны, а долгосрочная стабильность цен достигается в случае, когда темп роста денежной массы соответствует темпу роста реального производства.
Если вместо уравнения (8) использовалось уравнение (8-й), то итоговое уравнение будет иметь следующий вид:
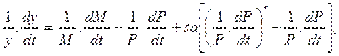 (9-a)
(9-a)
где у — реальный доход.
Для стационарного режима получаем:
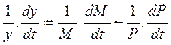 - эквивалентное уравнению (10).
- эквивалентное уравнению (10).
Модель ничего не говорит о влиянии денег на цены и уровень производства в отдельности. Этот аспект был рассмотрен в рамках так называемой теоремы об ускорении, которая явилась обобщением модели номинального дохода.
Фридмен ввел функции, описывающие изменения цен и реального дохода. Переменными этих функций являлись: изменения номинального дохода, ожидаемых цен и ожидаемого реального дохода, а также реального дохода и его ожидаемого значения. Эти функции могут быть представлены следующим образом:
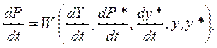 (11)
(11)
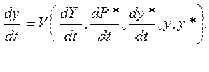 (12)
(12)
Объединив эти уравнения с уравнением (9), Фридмен получил систему трех линейных дифференциальных уравнений, которая описывает реакцию системы на возмущения, вызванные дополнительной эмиссией денег.
Если темп роста денежной массы увеличивается, возрастает расхождение между действительным и ожидаемым темпом роста номинального дохода. Уравнения (11) и (12) показывают, как это расхождение «распределяется» между ростом цен и реального дохода.
При некоторых упрощающих предположениях можно ожидать, что данная система будет описывать затухающий колебательный процесс, т.е. когда воздействие одноразового увеличения денежной массы прекращается, через некоторое время экономика возвращается на траекторию устойчивого роста. Колебания возобновляются, когда системе сообщается новый импульс в виде ускоренного роста денежной массы.
Иными словами, для того чтобы денежная политика влияла на реальное производство, необходимо увеличивать массу денег возрастающим темпом. В этом и состоит теорема об ускорении.
Изложена в двух работах Фридмена: Friedman M. A Theoretical Framework for Monetary Analysis // Journal of Political Economy. 1970. № 2; A Monetary Theory of Nominal Income // Journal of Political Economy. 1971. № 2.
В общем виде адаптивные ожидания могут быть заданы следующей формулой: X* = Х^ + а(Х* ^ — Х^, которая показывает, что текущий прогноз зависит от прошлого значения переменной и ошибки прогноза, относительно прошлого значения переменной. Легко видеть, что эта формула эквивалентна следующей: Х*^ = £ ЬХ^, где А. - коэффициенты, полученные из коэффициентов исходного уравнения.
Дата: 2018-11-18, просмотров: 385.