При разработке морфологических таблиц на основе функционального анализа систем достаточно было выявить функции подсистем, образующих исследуемую систему в целом, и подобрать для каждой функции альтернативы конкретных реализаций. Данный вид морфологических таблиц хотя и дает возможность проведения многокритериальной оценки альтернатив и выбора рациональной целостной системы, однако в ряде исследовательских задач недостаточно глубоко вскрывает морфологию системы. Устранить этот недостаток можно путем использования в морфологических таблицах классификационных признаков для описания альтернатив (табл. 5.2).

Чтобы построить морфологические таблицы на основании классификационных признаков, требуется разработать для каждой обобщенной функциональной подсистемы функциональную классификацию. После формирования классификаций осуществляется описание альтернатив каждой функции соответствующими признаками и значениями этих признаков, т. е. составляются классификационные образы альтернатив. Обработка таких морфологических таблиц проводится с использованием подходов кластерного анализа.

Таблица 5.2

Представление знаний об альтернативе в виде множества классификационных признаков

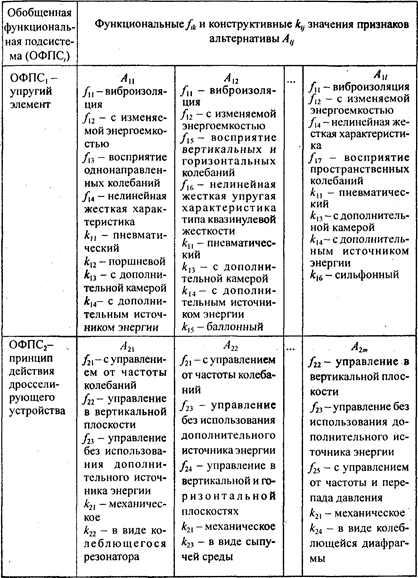
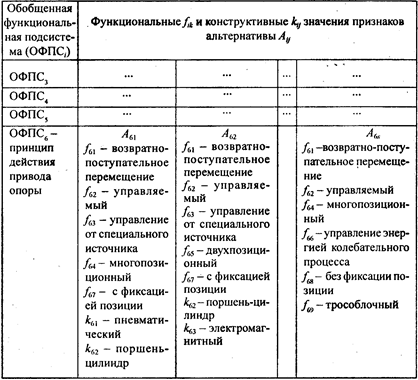
Кластерный анализ морфологических множеств

Основы кластерного анализа систем

Для выявления закономерностей строения сложных систем целесообразно в первую очередь собранные данные разложить "по полочкам", классифицировать. Вопросы кластерного анализа рассмотрены в учебнике А. М. Дуброва, В. С. Мхитаряна, Л. И. Трошиной [З].

Стремление собрать похожие объекты "в кучу" вполне понятно, поскольку именно классификация помогает исследователю ориентироваться в огромном многообразии объектов и тем самым является средством экономии памяти. В общем виде классификации позволяют, с одной стороны, относить объекты к одному из классов, а с другой — формировать сами "образы", число которых заранее может быть неизвестно.

Таким образом, анализ структуры данных — необходимый этап проводимых исследований. Особую актуальность классификационные построения приобретают при разработке новых информационных технологий, предназначенных для исследования сложных систем.

Рассмотрению подлежат в основном детерминистские методы построения и исследования систем-классификаций, основанные на качественных и количественных признаках.

Системы-классификации

Система определяется как непустое множество объектов (или несколько таких множеств), между которыми установлены некоторые отношения. Таким образом, в системе набор элементов рассматривается как целостное единство, обладающее интегративными свойствами и противостоящее окружению или среде.

Система может быть представлена пятеркой:

Если хотя бы один член пятерки изменяется во времени или пространстве, то система называется динамичной, в противном случае — статичной.

Системы-классификации — это результат классификационных построений на множествах объектов. Примерами таких систем могут являться множество описаний объектов с заданным отношением эквивалентности, т.е. принадлежности к одному и тому же классу; множество классов с заданным отношением иерархии; множество классификаций с заданным отношением доминирования и т.д. В приведенных примерах указаны системы-модели, т.е. некоторые абстрактные аналоги реальных систем, которые значительно проще последних по большинству аспектов, исключая самые важные для конкретного рассмотрения. Системы-классификации сочетают субъективные и объективные начала, так как человек при классификационных построениях учитывает лишь ограниченное число признаков из бесконечного числа возможных. Таким образом, для бесконечного набора, которым обладает реальный объект, существует также бесконечное множество вариантов выбора ограниченных наборов.

Следовательно, если множество признаков, учитываемое на объектах, является системой описания, а множество значений каждого из учитываемых признаков на конкретных объектах — описанием этих объектов, то аналоги-модели объектов (в частности, системы-классификации) — это системы множеств, каждое из которых есть описание. Система-модель С = С ( I , R , A ^{( S )}, A ^{( ps )} , A ^{( SP )} ) является образом системы-оригинала С' = С ( I ', R', А^{( S ')} ), A ^{( RS ')}, A ^{( SR ')} ). Отображение множества С' на множество С является гомоморфным, если С имеет тот же состав, что и С' (обратное неверно). Из сказанного видно, что система-модель содержит меньшее число элементов и связей, чем система-оригинал, но все элементы и связи, которые имеются в модели, правильно копируют прототип.

Для выбора "правильной модели" не существует формальной процедуры, она определяется целями классификационных построений и уровнем знаний конкретного исследователя.