| Номер итерации | Состояние множества альтернатив А i | Альтернативы, определяющие генерируемую комбинацию | ||
| 1 | А1 "Л" | А2 "Л" | А3 "Л" | - |
| 2 | А1* "И" | A 2 "Л" | А3 "Л" | A 1 |
| 3 | А1 "Л" | А2* "и" | А3 "Л" | A2 |
| 4 | А1* "И" | А2 "И" | А3 "Л" | А1А2 |
| 5 | А1 "Л" | А2 "Л" | А3* "И" | А3 |
| 6 | А1* "И" | А2 "Л" | А 3 "И" | A1A3 |
| 7 | A1 "Л" | А2* "И" | А3 "И" | A 2 A 3 |
| 8 | А1* "И" | А2 "И" | A3 "И" | A1A2A3 |
* - отмечен последний изменившийся на итерации признак.
Алгоритм определения комбинации альтернатив, обеспечивающей оптимальное распределение ресурса, имеет следующий вид.
Шаг 1. Определяется М альтернатив, для каждой из которых устанавливается требуемый ресурс и вычисляется относительная эффективность.
Шаг 2. Генерируются все парные, тернарные, М-1 комбинации альтернатив.
Шаг 3. Для каждой сгенерированной комбинации определяются суммарные значения: требуемого ресурса, относительной эффективности и относительной эффективности на единицу требуемого ресурса.
Шаг 4. Определяется искомая комбинация альтернатив с учетом задаваемой целевой функции.
Рассмотрим пример распределения ресурса на комбинации альтернатив, представляющих компьютерные бухгалтерские программы.
Заданы четыре компьютерные бухгалтерские программы: А1 — "1C: Бухгалтерия 6.0. ПРОФ" для Windows 95; А2 — "INFO-Бухгалтер"; А3 — Комплексная система "INOTEC Бухгалтер"; А4 — Бухгалтерская система "ПАРУС".
Относительная эффективность (полезность) бухгалтерских программ оценена по комплексу иерархически упорядоченных критериев качества с трех точек зрения: программиста, сопровождающего функционирование программ; бухгалтера, ведущего бухгалтерский анализ на предприятии; руководителя предприятия, использующего результаты бухгалтерского анализа для принятия решений (рис. 2.21).
Методом анализа иерархий определен вектор приоритетов альтернатив, характеризующий их относительную эффективность. Относительная эффективность бухгалтерских программ и требуемые для их приобретения ресурсы (в условных денежных единицах) приведены в табл. 2.12.
Таблица 2.12
Исходные данные по эффективности и требуемому ресурсу
| Параметр | Альтернатива Ai | |||
| А1 | А2 | А3 | А4 | |
| Относительная эффективность | 0,20 | 0,30 | 0,35 | 0,15 |
| Требуемый ресурс | 5 | 5 | 10 | 3 |
Таблица 2.13
Результаты распределения ресурса
| Параметр | Комбинация альтернатив | ||||||
| А1А2 | А1А3 | А1А4 | A1A2A3 | A1A3A4 | A2A3A4 | A1A2A3 A 4 | |
| Суммарная, эффективность комбинации | 0,50 | 0,555 | 0,35 | 0,85 | 0,70 | 0,80 | 1,0 |
| Требуемый ресурс на комбинацию | 10 | 15 | 8 | 20 | 18 | 18 | 23 |
| Эффективность на единицу ресурса | 0,050 | 0,037 | 0,044 | 0,043 | 0,039 | 0,044 | 0,043 |
Все возможные комбинации, состоящие из двух, трех и четырех альтернатив, суммарная эффективность комбинаций, требуемый на каждую операцию ресурс и эффективность на единицу ресурса приведены в табл. 2.13.
Требуется определить такие комбинации альтернатив, на которые наиболее целесообразно распределить имеющийся ресурс (15 единиц ресурса) с учетом целевых функций (2.12) и (2.13) при условии min (Ри - Рт).
Искомыми комбинациями альтернатив для первой целевой функции является А1 А2, а для второй — А1 А3.
Основные понятия
1. Иерархия.
2. Шкала отношений.
3. Предпочтения.
4. Парные сравнения.
5. Матрицы попарных сравнений.
6. Собственный вектор и собственное значение матрицы попарных сравнений.
7. Однородность суждений.
8. Индекс и отношение однородности матрицы попарных сравнений альтернатив.
9. Синтез приоритетов на иерархии.
10. Однородность иерархии.
11. Принятие решений при учете мнений нескольких экспертов.
12. Сравнение объектов методами стандартов и копирования.
13. Иерархии с различными числом и составом альтернатив под критериями.
14. Многокритериальное прогнозирование социально-экономических систем.
15. Функционально-стоимостный анализ методами анализа иерархий.
16. Рациональное распределение ресурсов методами анализа иерархий.
Контрольные вопросы и задания
1. Какой тип иерархии используется в методе анализа иерархий?
2. Дайте численную и лингвистическую характеристики шкалы отношений.
3. Постройте матрицу попарных сравнений для семи альтернатив.
4. Составьте алгоритм и программу для расчета на ЭВМ собственного вектора и собственного значения матрицы попарных сравнений.
5. Составьте алгоритм и программу для определения индекса и отношения однородности матрицы попарных сравнений.
6. Разработайте универсальный алгоритм и программу для решения задачи синтеза приоритетов для иерархий, элементы которых могут иметь различные связи.
7. Разработайте алгоритм и программу для оценки однородности иерархии, имеющей любую структуру.
8. Разработайте алгоритм и программу для решения задачи синтеза приоритетов на иерархии с учетом мнений нескольких экспертов.
9. В каких ситуациях объекты сравниваются методами стандартов и копирования?
10. Приведите прикладные примеры иерархий с различным числом альтернатив под критериями.
11. Разработайте алгоритм и программу синтеза приоритетов в иерархиях с различным числом альтернатив под критериями.
12. Примените метод анализа иерархий для решения прикладных задач выбора и прогнозирования в различных сферах экономики, например, при снижении риска в антикризисном управлении фирмой.
13. Смоделируйте механизм регионального и городского бюджетов, перераспределите финансовые и другие виды ресурсов, в том числе для реализации крупных региональных программ.
14. Примените метод анализа иерархий для поддержки принятия решений во внешнеэкономической сфере.
15. Разработайте рациональную программу в социальной и инвестиционной сферах.
16. Примените методы принятия решений для разрешения политических и этнических конфликтов.
17. Проведите функционально-стоимостный анализ организационной структуры и управленческой деятельности предприятия.
18. Осуществите рациональное распределение ресурсов с использованием системных методов между альтернативами исследуемой экономической системы.
Литература
1. Макеев С. П., Шахнов И.Ф. Упорядочение объектов в иерархических системах // Известия АН СССР, Техническая кибернетика. — 1991.—№ З.—С. 29—46.
2. Caamu Т. Принятие решений. Метод анализа иерархий: Пер. с англ. — М.: Радио и связь, 1989. — 316 с.
3. Сваткин М. 3., Мацута В. Д., Рахлин К. М. Группы качества на машиностроительных предприятиях. —Л.: Машиностроение, 1988. — 141 с.
4. Влчек Р. Функционально-стоимостный анализ в управлении: Сокр. пер. с чеш. — М.: Экономика, 1986. — 176 с.
5. Карпунин М. Г., Любинецкий Я. Г., Майданчик Б. И. Жизненный цикл и эффективность машин. — М.: Машиностроение, 1989. — 312 с.
6. Карпунин М. Г., Майданчик Б. И. Функционально-стоимостный анализ в электротехнической промышленности. — М.: Энергоиздат, 1984. —288 с.
7. Скворцов Н. Н., Омельченко Л. Н. Организация функционально-стоимостного анализа на машиностроительных предприятиях. — Киев: Технiка, 1987. — 112 с.
ГЛАВА 3.
АНАЛИТИЧЕСКОЕ ПЛАНИРОВАНИЕ НА ОСНОВЕ МЕТОДА АНАЛИЗА ИЕРАРХИЙ
Планирование является социальным процессом, сводящим то, что считается наиболее вероятным исходом ситуации при заданных текущих действиях, политиках и силах окружающей среды, с тем, что представляется как желательный исход, который, в свою очередь, требует новых действий и политик. Таким образом, планирование — сводящий процесс, поскольку оно уменьшает расхождение между вероятным и желаемым (оптимальным) будущим.
Планирование само по себе является системой, которая имеет назначение (достижение желаемой цели), функции (исследовать среду, ситуацию, структуру, выбрать альтернативы и оценить действия), потоки (информация между специалистами по планированию и пользователями) и структуру (общий план, в пределах которого специалист по планированию сближает наиболее вероятный и желаемый результаты, используя обучение и обратную связь в форме суждений и данных для переоценки результатов).
3.1. Принципиальные подходы к решению задач планирования
Можно выделить три принципиальных подхода к планированию [1-9].
Удовлетворенческое планирование предполагает достижение неплохих результатов, но не обязательно наилучших. Уровень, которого необходимо достичь для "удовлетворения", определяется как уровень, на который соглашаются лица, принимающие решения. Такое планирование редко приводит к радикальным переменам. Как правило, оно порождает консервативные планы, исправляющие только явные недостатки и не способствующие росту и развитию.
Оптимизационное планирование направлено на реализацию программ наилучшим образом. Оптимизационное планирование более полезно в тактическом планировании, чем в стратегическом, поскольку первый случай характеризуется полной определенностью исходных данных в настоящем и будущем, а для такой ситуации наилучшим образом приспособлены, как известно, методы оптимизации. Для оптимизационного планирования характерны следующие задачи:
• минимизация ресурса, необходимого для достижения намеченного уровня эффективности;
• максимизация эффективности, которой можно достичь с имеющимся запасом ресурса;
• максимизация отношения эффективности к затратам.
Аналитическое стратегическое планирование направлено на решение задач, характеризующихся в будущем неопределенностью и незнанием.
Аналитическое стратегическое планирование — процесс обучения и эволюции, т.е. процесс проецирования вероятного или логического будущего (обобщенного сценария) и идеализированных желаемых будущих состояний.
Все планы имеют три общих компонента — начальное состояние, цель (или конечное состояние) и средства, связывающие эти два состояния. Цель процесса планирования — соединить компоненты за наименьшую цену, чтобы достигнуть наибольшей эффективности.
Первый компонент — начальное состояние — определяет начальное состояние людей, управляющих определенными ресурсами; экономическое, политическое и социальное положение общества; ограничения природы и окружающей среды и т.п.
Второй компонент — цель — это желаемая величина, которую надеются достигнуть.
Третий компонент — средства, т. е. сам план, с помощью которого происходит переход от начального состояния к цели.
Выделяются три отличающихся процесса планирования: в прямом направлении, обратном направлении, одновременно в прямом и обратном направлениях.
Процесс планирования в прямом направлении направлен только в одну сторону. Он представляет собой упорядоченную во времени последовательность событий, которая начинается в момент времени t = 0 и заканчивается в будущем в момент времени t = Т. В прямом процессе рассматриваются текущие факты и предположения, порождающие логический исход (сценарий).
Процесс планирования в обратном направлении начинается с желаемого исхода в момент времени T, и затем процесс рассматривается в обратном направлении во времени, чтобы оценить факторы и промежуточные исходы, которые требуются для достижения желаемого исхода. Таким образом, обратный процесс планирования обеспечивает средствами контроля и управления прямой процесс при движении в направлении желаемого состояния.
Процесс планирования, осуществляемый одновременно в прямом и обратном направлениях, основан на классической теории планирования, которая предполагает наличие двух целей планирования.
Первая цель — это логическая или достижимая цель, при постановке которой подразумевается, что предположения и факторы, воздействующие на исход, останутся существенно неизменными по отношению к настоящему состоянию.
Вторая цель — желаемая, достижение которой требует больших изменений на входах. Эти изменения нужно не только осуществить, но и сделать необратимыми, несмотря на первоначальное поведение системы.
Принцип интегрированного прямого и обратного процессов иерархического планирования осуществляется следующим образом. Сначала проектируется вероятное будущее (первый прямой процесс). Далее в качестве цели принимается желаемое будущее и вырабатываются новые политики (первый обратный процесс), которые присоединяются к набору существующих, и с учетом этих изменений вновь проектируется будущее (второй прямой процесс). Проводится сравнение двух вариантов вероятного будущего и желаемого будущего, соответствующих первому и второму прямому и первому обратному процессам планирования относительно их главных характеристик.
3.2. Представление процесса планирования в виде иерархии
Поскольку в основе стратегического аналитического планирования лежит механизм прямого и обратного процессов, рассмотрим его более подробно с учетом метода анализа иерархий.
Прежде всего следует отметить, что иерархические системы планирования состоят из специфических элементов, имеющих определенное толкование. К указанным элементам относятся: фокус иерархии, акторы, цели, политики, исходы и обобщенный исход. Под фокусом иерархии понимается общая цель исследуемой проблемы. Данный иерархический уровень может состоять из горизонтов (нескольких интервалов времени). Акторами называются действующие силы, с различной степенью воздействующие на исход. Цели—желаемые пределы или величины, которых надеются достигнуть. Под политиками понимаются санкционированные средства достижения целей, предоставляемые с помощью общепринятых процедур принятия решений. Исходы — это потенциальные состояния системы, которые получены после применения политик. Обобщенный исход позволяет интегрировать значения отдельных исходов для оценки последствий принимаемых при планировании решений.
Введем обозначения множеств элементов и собственно элементов, определяющих иерархические уровни. Множества элементов обозначаются прописными буквами русского алфавита, а элементы — строчными буквами:
Фij—фокус иерархии;
Сij = {сm ij} — множество сил;
АКij = {акn ij} — акторы;
Цij = {цr ij} — пели;
Пij = {пr ij} — политики;
Иij = {иs ij} — исходы;
Прij = {пptij} — проблемы.
Для дальнейших рассуждений введем также обозначения, характеризующие интегральную оценку обобщенного исхода (ОИфij ) и интегральную оценку обобщенного исхода относительно конкретного актора (ОИАКij ).
В приведенных выше обозначениях первый нижний индекс (i) указывает направление процесса (прямой процесс или обратный), на котором впервые появился элемент иерархии. При этом i = 1 соответствует процессу планирования в прямом направлении, а i =2 — процессу планирования в обратном направлении. Второй нижний индекс j = 1, k указывает порядковый номер процесса планирования в прямом и обратном направлениях. Верхние индексы обозначают порядковый номер элемента на соответствующем уровне или подуровне иерархии.
При исследовании иерархий рассчитываются векторы приоритетов исходов в прямом процессе (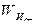 
) и векторы приоритетов целей ( 
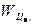) или политик (программ) ( 
) в обратном процессе планирования относительно элементов иерархии. Обозначения этих векторов приведены в табл. 3.1, где верхние индексы указывают элементы иерархии, относительно которых они рассчитаны.
Таблица 3.1
Дата: 2018-11-18, просмотров: 285.
