Результаты наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными.
При большом числе результатов наблюдений (n>40) данная задача решается в следующем порядке.
Весь диапазон полученных результатов наблюдений Xmax ... Xmin разделяют на r интервалов шириной 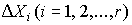 и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
Отношения
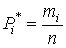
|
где n - общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i-й интервал. Распределение частот по интервалам образует статистическое распределение результатов наблюдений.
Если теперь разделить частость на длину интервала, то получим величины
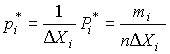
|
являющиеся оценками средней плотности распределения в интервале 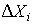 .
.
Отложим вдоль оси результатов наблюдений (рис.11) интервалы 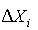 в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной
в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной 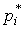 . Полученный график называется гистограммой статистического распределения.
. Полученный график называется гистограммой статистического распределения.
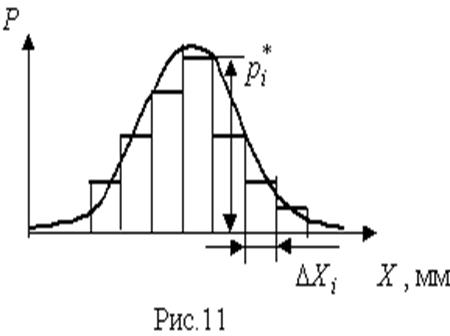
Площадь суммы всех прямоугольников равна единице:
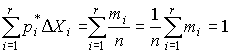
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, - к графику плотности распределения результатов наблюдений.
При построении гистограмм рекомендуется пользоваться следующими правилами:
1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл.3.
Таблица 3
|
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы.
3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.
Пример. Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты наблюдений лежат в диапазоне 8.911 - 8.927 мм, т. е. зона распределения результатов составляет 0.016 мм. Весь диапазон удобно разделить на восемь равных интервалов через 0.002 мм. В табл.4 приведены частоты mi, частости 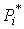 и плотности
и плотности 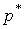 статистического распределения.
статистического распределения.
Таблица 4
|
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения, или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическим распределением. Одним из методов решения этой задачи является метод моментов. При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое гистограммой, приведенной на рис.11, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсий, вычисленным по опытным данным. В предыдущем примере 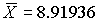 мм,
мм, 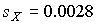 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
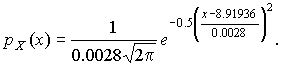
Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе?
Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению 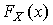 с плотностью
с плотностью 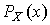 .
.
Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U, представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами:
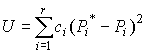 , ,
|
где 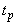 – коэффициенты, называемые весами разрядов;
– коэффициенты, называемые весами разрядов; 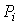 – теоретические вероятности, определяемые как
– теоретические вероятности, определяемые как
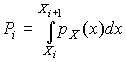 , ,
|
Здесь 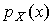 – предполагаемая плотность распределения.
– предполагаемая плотность распределения.
Мера расхождения U является случайной величиной и, независимо от исходного распределения подчиняется 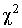 -распределению с k степенями свободы. Если значения всех частот
-распределению с k степенями свободы. Если значения всех частот 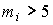 , число измерений стремится к бесконечности, а веса
, число измерений стремится к бесконечности, а веса 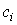 выбираются равными
выбираются равными 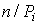 . Число степеней свободы распределения k = r - s, где
. Число степеней свободы распределения k = r - s, где 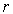 – число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости
– число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости 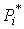 .
.
Систематическая погрешность – составляющая погрешности, которая остаётся постоянной при повторных измерениях одной и той же величины.
Причины возникновения систематической погрешности:
- неисправность измерительного устройства;
- несовершенство метода измерения;
- неправильная установка измерительного устройства;
- отступление условий эксплуатации от нормальных;
- особенности оператора производимого измерения;
- и др.
Инструментальная погрешность – составляющая погрешности измерения, зависящая от погрешностей применяемых средств измерений, т.е. обусловлена особенностью конструкции измерительного устройства, неточностью градуировки, шкалы, а также неправильностью установки измерительного устройства. Инструментальная погрешность, как правило, указывается в паспорте на средство измерения и может быть оценена в числовом выражении.
Методическая погрешность – обусловлена несовершенством применяемого метода измерения , неточностью формул и математических зависимостей, описывающий данный метод измерения, а также влиянием средства измерения на объект свойства которого изменяются.
Грубая погрешность изме рения - погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность.
Погрешность отсчитывания - составляющая погрешности измерения, происходящая от недостаточно точного отсчитывания показаний средства измерений.
Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.
Примеры. Погрешность от несоответствия действительного значения меры, с помощью которой выполняют измерения, ее номинальному значению; погрешность вследствие постепенного уменьшения силы рабочего тока в цепи электроизмерительного потенциометра.
Систематическая погрешность может быть выявлена и устранена путём анализа возможных источников её возникновения в каждом конкретном случае.
Субъективная погрешность обусловлена несоответствием органов зрения оператора производимого измерение (косоглазие). Для устранения этой погрешности все измеряемые устройства снабжают дополнительными шкалами (зеркальными).
Все системные погрешности классифицируются на две группы:
- постоянные (проще всего устраняются путём коррекции показаний с помощью корректора);
- закономерно изменяющиеся:
1) прогрессирующие;
2) периодические;
3) изменяются по сложному закону.
Причинами возникновения закономерно изменяющихся погрешностей являются – колебания в широком диапазоне, изменение параметров окружающей среды (температура, влажность, запылённость и так далее), а также изменение других влияющих величин по сложному законы.
Прогрессирующие погрешности являются сложными и непредсказуемыми, так как могут либо возрастать, либо убывать в отличии от периодической погрешности, которая появляется и исчезает с каким либо периодом.
Методы устранения систематической погрешности могут быть разбиты на основные и специальные.
К основным относятся:
1) термостабилизация;
2) термоизоляция;
3) установка специальных экранов защищающих от действия внешних полей;
4) использование в конструкциях средств измерения амортизирующих устройств;
5) применение стабилизаторов питающего напряжения и др.
К специальным методам устранения системной погрешности относятся:
1) метод замещения, при котором измеряемая величина заменяется известной величиной, таким образом, что составление и действие ИП остаётся неизменным, а измерение при этом производится дважды;
2) метод противопоставления, при этом методе измеряемая величина заменяется (противопоставляется) известной величиной задаваемой мерой;
3) метод компенсации погрешности по знаку – обычно применяется, когда имеет место направляемая или знакочередующая погрешность.
4) метод постоянных наблюдений – в соответствии с этим методом измерение физической величины и оценка системной погрешности производится трижды, с использованием образцовой меры на входе измеряемого устройства;
5) метод периодических наблюдений – применяется в случае периодической составляющей системной погрешности и направлен на её устранение.
Систематическую погрешность, как правило, полностью устранить не представляется возможным, однако если известна функциональная зависимость влияющей величины от других факторов, то эта составляющая погрешности может быть оценена и оставаться достаточно маленькой.
Случайная погрешность – составляющая погрешности, которая изменяется случайным образом при повторных измерениях одной и той же величины. Причиной случайной погрешности является одновременное действие многих случайных факторов, каждый из которых в отдельности мало влияет.
Примеры. Погрешность вследствие вариации показаний измерительного прибоpa; погрешность округления при отсчитывании показаний измерительного прибора.
В ряде измерений результат одного отдельно взятого измерения может резко отличатся от результатов других измерений из-за ошибок оператора, толчков, действия сильных помех, изменение электрического контакта и других причин. Этот результат следует отнести к грубым промахам и исключить из дальнейшей статической обработки.
Промахи – это грубые ошибки, например, ошиблись при записи показаний прибора (вместо 10,2 записали 102 или 202), неправильно приложили начало линейки к измеряемому объекту, промахи обусловлены, как правило, недостатком внимания и аккуратности исследователя.
Случайная погрешность может быть оценена и частично снижена путём правильной обработки методами математической статистики, а также методами вероятности.
Аддитивная погрешность – погрешность измерения, которая при всех значениях входной измеряемой величины Х приводит к изменению значения выходной величины У на одну и ту же величину большую или меньшую от номинального значения.
Причиной возникновения мультипликативной погрешности является изменение коэффициента усиления усилителя, изменение коэффициента деления делителя напряжения и другие причины.
Все погрешности СИ классифицируются на: основные погрешности СИ, которые имеют место и характеризуются нормальными условиями эксплуатации измеряемого устройства (нормальное относительное давление, температура, влажность и другие причины).
Дополнительные погрешности имеют место в условиях эксплуатации, в условиях, отличающихся от нормальных по давлению, влажности, температуре и других. В зависимости от изменения входного сигнала во времени все погрешности СИ классифицируются на: статическую погрешность – не зависит от скорости изменения измеряемой величины во времени (состояние СИ при котором значения входных и выходных сигналов не изменяется во времени).
Аддитивная 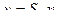 Мультипликативная
Мультипликативная 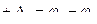
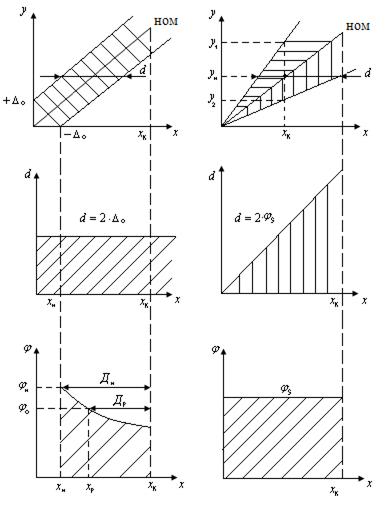
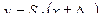
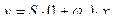
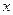 - измеряемая величина;
- измеряемая величина;
 `- выходная величина;
`- выходная величина;
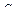 - чувствительность;
- чувствительность;
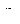 - относительная погрешность чувствительности;
- относительная погрешность чувствительности;
 - интервал неопределённости;
- интервал неопределённости;
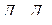 - полный и рабочий диапазоны измерения;
- полный и рабочий диапазоны измерения;
 - начальное значение измеряемой величины;
- начальное значение измеряемой величины;
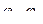 - начальное и заданное значения относительной погрешности;
- начальное и заданное значения относительной погрешности;
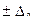 - абсолютная погрешность нуля (аддитивная погрешность).
- абсолютная погрешность нуля (аддитивная погрешность).
Динамическая погрешность средства измерений - разность между погрешностью средства измерений в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени.
В ряде измеряемых устройств существует погрешность гистерезиса (запаздывание), погрешность обратного хода. Является наиболее существенной и трудно устранимой погрешностью, которая выражается в виде реальной функции преобразования.

Причины погрешности гистерезиса:
1) наличие люфта в механических передающих элементах;
2) сухое трение (в керновых узлах);
3) упругое последействие в упругих чувствительных элементах;
4) явление поляризации в пьезоматериалах.
Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины. Эта погрешность может задаваться в единицах измеряемой величины; в виде уравнения; с помощью таблиц.
Относительная погрешность – отношение абсолютной погрешности к значению измеряемой величины, выраженному в процентах.
1) 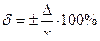
2) С помощью уравнения прямой:
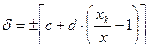 , где
, где
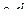 - постоянные коэффициенты, определяющие положение измеряемой величины.
- постоянные коэффициенты, определяющие положение измеряемой величины.
Xk – конечное значение измеряемой величины по диапазону 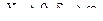
Приведенная погрешность – отношение абсолютной погрешности к нормированному значению измеряемой величины:
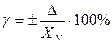
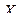 - нормированное значение измеряемой величины. В его качестве принимается для приборов имеющих одностороннюю, равномерную или степенную шкалу, конечное значение по шкале для приборов с двухсторонней шкалой и с 0 по середине принимается сумма конечных значений.
- нормированное значение измеряемой величины. В его качестве принимается для приборов имеющих одностороннюю, равномерную или степенную шкалу, конечное значение по шкале для приборов с двухсторонней шкалой и с 0 по середине принимается сумма конечных значений.
12. Правила суммирования погрешностей
Систематические погрешности, если они известны или достаточно точно определены суммируют алгебраически, т.е. с учетом собственного знака. Нередко систематическая погрешность по своей природе носит характер случайной, иногда при суммировании все погрешности рассматриваются как случайные. Случайные погрешности суммируют с учетом их взаимных корреляционных связей. Обычно информация о мере корреляции связей отсутствует, поэтому на практике рассматривают 2 крайних случая – когда коэффициент корреляции =0 или =1. При этом некоррелированные погрешности, т.е. вызванные взаимонезависимыми источниками или причинами, суммируются геометрически. δ∑=√(∑i=1Nδi2). Случайные погрешности сильно или жестко коррелированные (коэффициент корреляции=1) суммируются с учетом следующих предпосылок. Если данная причина вызывает в различных узлах прибора измерение погрешности в одном и том же направлении, то погрешности складываются δ(инд.∑)=δ1+δ2. Если же изменение противоположно, то погрешности вычитаются δ(инд.∑)=│δ1- δ2│.
13. Метрологические характеристики средств измерения в статике
Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками [9,10]. Перечень важнейших из них регламентируется ГОСТ “Нормируемые метрологические характеристики средств измерений”. Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации посредством отдельных средств измерений или совокупности средств измерений, например автоматических измерительных систем.
Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования (иначе называемая функцией преобразования или градуировочной характеристикой). Она устанавливает зависимость 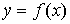 информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала.
информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала.
Работа СИ в статике характеризуется следующими основными метрологическими характеристиками:
Уравнение преобразования – связывает функционально и однозначно выходную и входную измеряемые величины. Уравнение преобразования может задаваться таблично, графиком или функциональной зависимостью. Уравнение преобразования имеет следующий вид:
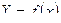 .
.
Уравнение преобразования может быть линейным и нелинейным.
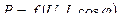 ,
,  ,
, 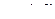 (если линейное)
(если линейное)
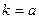 - статический коэффициент преобразования.
- статический коэффициент преобразования.
Для линейной функции преобразования  ,
, 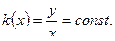
Для нелинейной функции преобразования  .
.
Чувствительность – характеризует степень реагирования СИ на изменение входной величины:
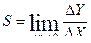 ,
, 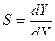 .
.
Очень часто в измерительных устройствах применяют относительную чувствительность:
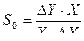
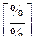 .
.
Порог чувствительности – это изменение входной величины вызывающее наименьшее обнаруживаемое данным СИ без каких-либо дополнительных устройств измерения выходной величины.
Функция преобразования – характеризует связь между информативным входным параметром или информативных параметров выходной величины.
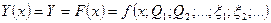
где: 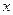 - измеряемая величина;
- измеряемая величина;
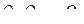 - параметры цепи преобразования;
- параметры цепи преобразования;
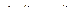 - погрешности преобразования.
- погрешности преобразования.
Различают номинальную функцию преобразования, которая носит название – градуировочная характеристика и реальная.
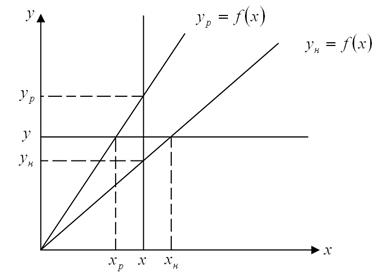
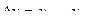 ,
, 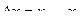
Градуировочная характеристика СИ строится при нормативных условиях эксплуатации (нормативное давление, влажность, температура и др.).
Каждой функции преобразования составляет свой коэффициент преобразования: нормативный или реальный. Коэффициент преобразования является более информативным параметром, чем чувствительность.
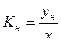 ,
, 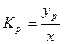 .
.
Для линейной функции преобразования 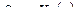
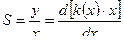
Постоянные измерения (преобразования):
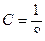 .
.
Верхний или нижний предел измерения (преобразования) – представляет собой наибольшее и наименьшее значение входной (выходной) величины, в которой могут быть изменены с нормативной погрешностью. Для СИ в статике нормируются уравнения преобразования и коэффициент преобразования.
Диапазон измерения 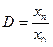 , где
, где  - наибольшее значение, которое измеряется или преобразуется,
- наибольшее значение, которое измеряется или преобразуется,  - наименьшее значение, которое измеряется или преобразуется.
- наименьшее значение, которое измеряется или преобразуется.
Диапазон измерения может быть разбит на несколько поддиапазонов с нормируемой погрешностью внутри поддиапазона. Различают полный диапазон и рабочий диапазон.
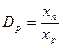 , где
, где 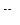 - нижний рабочий предел.
- нижний рабочий предел.
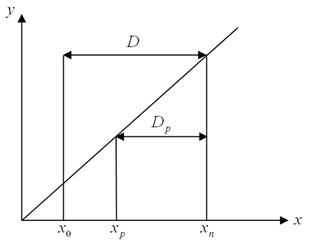
Показание СИ – значение величины определённой по отсчётному устройству и выражены в принятых единицах:
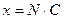 ,
,
где 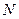 - отсчёт (неименованное число, полученное путём отсчёта отметок по шкале) или сигналы;
- отсчёт (неименованное число, полученное путём отсчёта отметок по шкале) или сигналы; 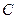 - постоянная измерения СИ (цена деления) (указывается на заводском шильнике).
- постоянная измерения СИ (цена деления) (указывается на заводском шильнике).
Кроме рассмотренных выше статических характеристик и параметров, применяются характеристики, косвенно связанные с метрологическими:
- надёжность – свойство СИ сохранять работоспособность и свои функциональные возможности в течение определённого периода времени ( 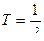 - наработка на отказ,
- наработка на отказ, 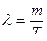 - параметр тока отказов). Надёжность СИ характеризуется безотказностью, ремонтопригодностью и долговечностью.
- параметр тока отказов). Надёжность СИ характеризуется безотказностью, ремонтопригодностью и долговечностью.
Кривая надёжности средства измерения:
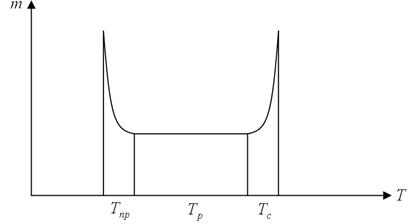
- стоимость.
- Степень согласования (сопряжения с другими измеряемыми устройствами).
14. Характеристики средств измерения в динамике
Дифференциальное уравнение - связывает измеряемую величину и выходную величину через динамические характеристики. СИ в динамике имеют характеристики отличные от характеристик в статике. Причиной появления динамических характеристик является появление динамических погрешностей, вызванных наличием в СИ всякого рода накопительных элементов (ёмкость, индуктивность и др.), а также инерционностью подвижных частей и узлов. Динамическая погрешность представляет собой разницу значений выходных величин реального и идеального преобразователей, когда на их входы подаётся одна и та же измеряемая величина. В отличии от реального преобразователя идеальный преобразователь осуществляет заданное преобразование без искажения измеряемой величины.
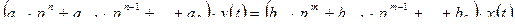
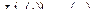
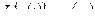
Передаточная функция
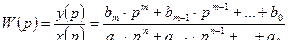 ,
,
если 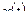 и
и 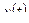 остаются величинами неизменяемыми, то
остаются величинами неизменяемыми, то 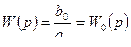 - статический коэффициент передачи.
- статический коэффициент передачи.
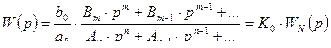
 - нормированная передаточная функция СИ.
- нормированная передаточная функция СИ.
Переходная функция – характеризует меру инерционности измеряемого преобразователя.
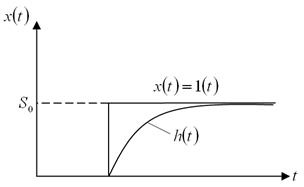
Весовая функция - представляет собой реакцию измеряемого преобразователя на входное воздействие в виде короткого импульса единичной площади.
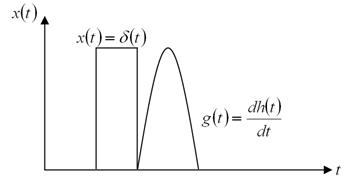
Операторная чувствительность:
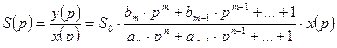 ,
,
где 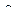 - статическая чувствительность.
- статическая чувствительность.
 ,
,
где  - коэффициент преобразования в динамике.
- коэффициент преобразования в динамике.
Пьезоэлектрические и некоторые другие преобразователи не имеют статической чувствительности, т.е. являются безинерционными. Для них:
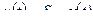 .
.
Комплексная чувствительность:
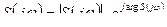 .
.
Обычно в измеряемой практике значение 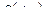 и
и 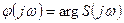 определяют по показаниям приборов (вольтметра, амперметра и фазометра). Таким образом, по своим динамическим характеристикам в зависимости от степени влияния частоты изменения измеряемого сигнала все измерительные преобразователи делятся на: безинерционные (идеальные) и инерционные (интегрированные, дифференциальные, апериодические, колебательные и т.д.).
определяют по показаниям приборов (вольтметра, амперметра и фазометра). Таким образом, по своим динамическим характеристикам в зависимости от степени влияния частоты изменения измеряемого сигнала все измерительные преобразователи делятся на: безинерционные (идеальные) и инерционные (интегрированные, дифференциальные, апериодические, колебательные и т.д.).
15. Структурные схемы средств измерения. Методы преобразования измеряемой величины
В структурных схемах СИ различают последовательные, параллельные, последовательно-параллельные и смешанные включения отдельных структурных элементов. Способ соединения измеряемых элементов при соответственном назначении определяем структурную схему СИ. Как правило в структурной схеме СИ в основе лежит какой-либо метод преобразования измеряемой информации.
1. Метод прямого преобразования
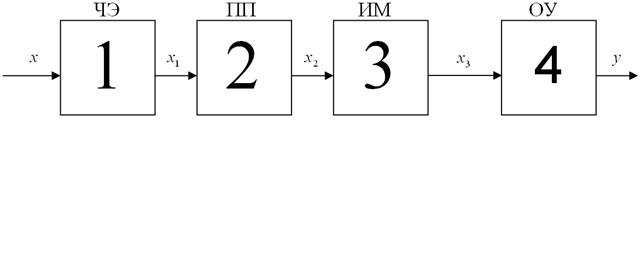
 - входная измеряемая величина;
- входная измеряемая величина;
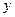 - выходная величина;
- выходная величина;
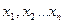 - промежуточные величины;
- промежуточные величины;
ЧЭ – чувствительный элемент;
ПП – первичный преобразователь;
ИМ – измерительный механизм;
ОУ – отсчётное устройство.
Метод прямого преобразования заключается в посланной передачи сигнала измеряемой информации от входа к выходу без ОС.
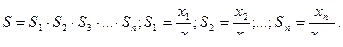
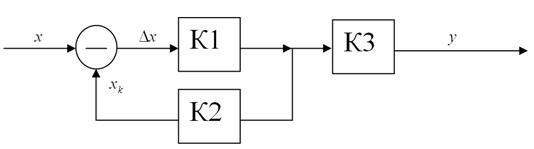
2. Метод уравновешивающего преобразования.
При этом методе входная измеряемая величина уравновешивается другой одноимённой величиной. При этом методе существуют два метода уравнений преобразований:
а) следящее преобразование предусматривает испытание ООС. Уравнение преобразования представляет собой статическую или астатическую характеристику. При статической характеристике входная величина уравновешивается выходной величиной в цепи ООС.
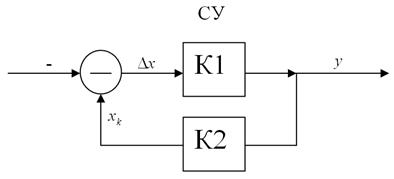
 - уравновешивающая величина;
- уравновешивающая величина;
К1, К2 – соответственно коэффициенты прямого и обратного преобразования;
СУ – сравнивающее устройство.
 .
.
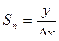 - чувствительность прямого преобразования.
- чувствительность прямого преобразования.
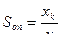 - чувствительность обратного преобразования.
- чувствительность обратного преобразования.
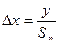 ;
; 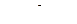 .
.
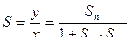 (1).
(1).
Анализ уравнения (1) показывает, что общая чувствительность определяется долей чувствительности ветви ОП.
 (2).
(2).
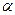 - коэффициент относительного уравновешивания:
- коэффициент относительного уравновешивания:
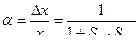 .
.
Суть уравновешивающего метода преобразования заключается в подаче на вход измеряемой цепи прямого преобразования величины 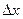 , которая благодаря большому значению коэффициента преобразования К1 и глубокой ООС сводится к столь малому значению, что можно принять
, которая благодаря большому значению коэффициента преобразования К1 и глубокой ООС сводится к столь малому значению, что можно принять 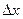 =0 и
=0 и  . Это рассуждение справедливо для астатических систем.
. Это рассуждение справедливо для астатических систем.
В статических системах 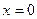 и
и 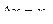 .
.
3. Развёртывающее уравновешивающее преобразование .
Суть сводится к следующему: с помощью источника компенсирующей величины задаётся величина  , которая изменяется по определённому закону до момента компенсации, когда
, которая изменяется по определённому закону до момента компенсации, когда 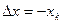 . При наступлении компенсации СУ воздействует на выходное устройство (ВУ) и источник компенсационной величины (ИКВ) фиксирует соответствующее значение
. При наступлении компенсации СУ воздействует на выходное устройство (ВУ) и источник компенсационной величины (ИКВ) фиксирует соответствующее значение  .
.
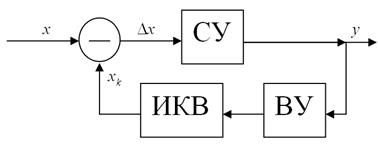
4. Метод комбинированного преобразования.
При это методе ООС охвачена часть ветви прямого преобразования
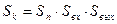 ,
,
где 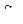 и
и 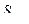 соответственно чувствительность элементов структурной схемы, включенной по замкнутой и разомкнутой измерительной схеме.
соответственно чувствительность элементов структурной схемы, включенной по замкнутой и разомкнутой измерительной схеме.
В качестве К3 используют узел отсчётного устройства.
16. Погрешность чувствительности средств измерения
Для нахождения погрешности чувствительности комплекса измерительных преобразователей необходимо прологарифмировать выражение для нахождения общей чувствительности отдельных функциональных звеньев входящих в комплекс.
1. Метод прямого преобразования.
 ;
;
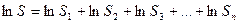 ;
;
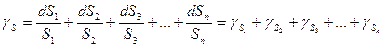 ;
;
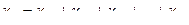 .
.
2. Метод уравновешивающих преобразований.
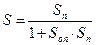 ;
;
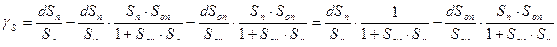

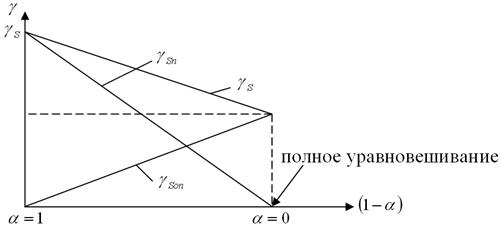
Анализ графика показывает, что при увеличении  до полного уравновешивания
до полного уравновешивания 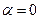 происходит уменьшение погрешности чувствительности ветви прямого преобразования, но одновременно увеличивается погрешность чувствительности ветви обратного преобразования. При полном уравновешивании общая погрешность чувствительности устанавливается
происходит уменьшение погрешности чувствительности ветви прямого преобразования, но одновременно увеличивается погрешность чувствительности ветви обратного преобразования. При полном уравновешивании общая погрешность чувствительности устанавливается  .
.
3. Комбинированное преобразование.
При комбинированном преобразовании необходимо учитывать погрешности в выходном устройстве.
17. Понятие класса точности. Нормирование точности средств измерения
По условиям, определяющим точность результата, измерения делятся на три класса:
- измерения максимально возможной точности, достижимой при существующем уровне техники.
К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например абсолютного значения ускорения свободного падения, гиромагнит-ного отношения протона и др.).
К этому же классу относятся и некоторые специальные изме-рения, требующие высокой точности.
- контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения.
К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения.
- технические измерения, в которых погрешность результата определяется характеристиками средств измерений.
Примерами технических измерений являются измерения, выполняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др.
По способу выражения результатов измерений различают абсолютные и относительные измерения.
Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.
Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате.
Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.
В качестве примера относительных измерений можно привести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м3 воздуха к количеству водяных паров, которое насыщает 1 м3 воздуха при данной температуре.
Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность.
Класс точности – обобщающая характеристика, определяемая пределами допустимой, основной и дополнительной погрешности, а её значение устанавливается в стандартах на отдельные СИ.Обозначается буквой К.
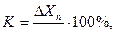 где
где
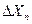 - максимальное значение абсолютной погрешности измерения;
- максимальное значение абсолютной погрешности измерения;
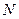 - предел измерения.
- предел измерения.
Действующий стандарт определяет ряд классов точности применяемых СИ.
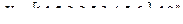 , где
, где 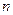 - показатель степени, который может принимать значения
- показатель степени, который может принимать значения 
На шкалах стрелочных приборов может указываться класс точности в виде дроби. 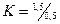 , где 1,5 – приведенная погрешность в конце шкалы; 0,5 – приведенная погрешность в начале диапазона.
, где 1,5 – приведенная погрешность в конце шкалы; 0,5 – приведенная погрешность в начале диапазона.
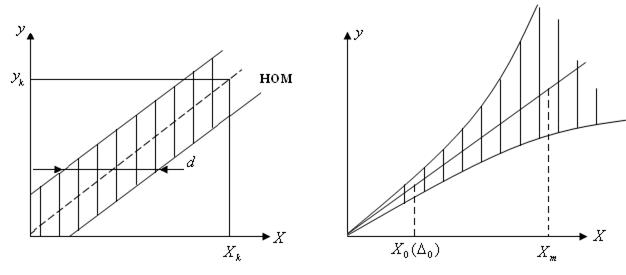
Погрешности узко-диапазонных СИ широкодиапазонных СИ.
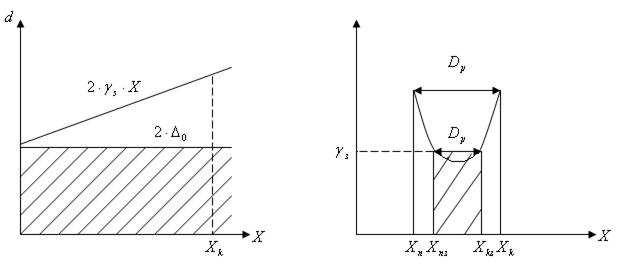
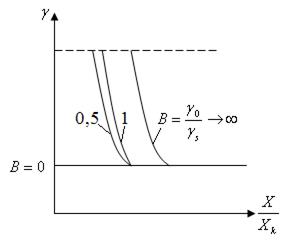
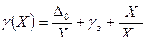
 - погрешность чувствительности;
- погрешность чувствительности;
 - относительная погрешность нуля.
- относительная погрешность нуля.
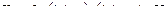 - уравнение преобразования.
- уравнение преобразования.
Нормирование проводится с целью исключения систематической погрешности из результата измерения. Существуют три метода нормирования точности:
1) трёхчленная формула для нормирования класса точности СИ:

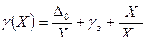 - применяется для широкополосных СИ.
- применяется для широкополосных СИ.
Для того, чтобы задать погрешность этим СИ необходимо знать нижний порог чувствительности 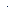 ;
; 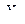 - верхний предел чувствительности;
- верхний предел чувствительности;  - погрешность чувствительности.
- погрешность чувствительности.
2) нормирование двухчленной формулой:
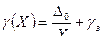
Применяется для узко-диапазонных СИ. Чаще всего при нормировании погрешностей двухчленной формулой пользуются другой записью:
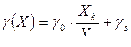
 - приведенная погрешность
- приведенная погрешность 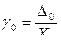 .
.
При нормировании двухчленной формулой различают 2 возможных случая:
а) 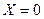 ; необходимо задать
; необходимо задать  .
.
б) 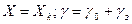 .
.
3) нормирование одночленной формулой:
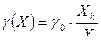
этот метод применяется для СИ, у которых имеется только аддитивная погрешность (постоянный интервал неопределённости). При таком нормировании погрешность определяется при  .
.
При нормировании одночленной формулой рекомендуют пользоваться определённым классом точности.
При измерении образцовым СИ зачастую вводят поправки для определения действительного значения измеряемой величины.
Поправка  , где
, где
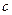 - поправка;
- поправка;
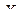 - действительное значение измеряемой величины;
- действительное значение измеряемой величины;
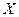 - измеряемое значение.
- измеряемое значение.
Цель поправки – устранить действие системной погрешности.
Таким образом, нормирование СИ по точности производится с целью оценки точностных характеристик СИ и в последующем точной оценки результата измерения с исправлением точностных характеристик СИ.
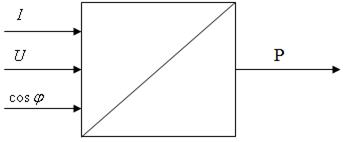
18. Преобразователи электрической измеряемой величины в электрическую величину
18.1 Измерительные выпрямители
Измерительные выпрямители – преобразователи переменного тока в постоянный с целью измерения переменного тока и удовлетворения определенным требованиям по погрешности и стабильности характеристик.
Выходная величина – постоянная составляющая, которая является функцией среднего, максимального или действующего значения входной величины.
Поэтому существуют измерительные выпрямители среднего, максимального или действующего значений.
Различают полупроводниковые, вакуумные и электромеханические выпрямители.
Коэффициент выпрямления стремится к единице в области малых частот, что уменьшает возможность измерений.
Кремниевые диоды до 1 МГц
Точечные до 100 МГц
Германиевые до 10МГц
Неуправляемые измерительные выпрямители
среднего значения

|

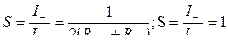
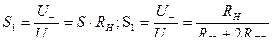
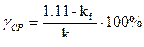
kf=1.11 – выпр. среднего значения
kf – коэффициент формы реальной кривой
Управляемые измерительные выпрямители
Имеют два входа:
- для подачи Ux;
- для подачи управляющего напряжения Uy той же частоты;
Iср зависит не только от Ux, но и от угла сдвига фаз между Ux и Uy.
Два типа управляемых измерительных выпрямителей:
- электромеханические;
- полупроводниковые;
Измерительные усилители
Измерительные усилители предназначены:
- для усиления измеряемых сигналов, т.е. для увеличения чувствительности (масштабное преобразование);
- для согласования сопротивлений сопрягаемых преобразователей;
- преобразователи напряжения в ток или тока в напряжение;
- для уменьшения потребления энергии от исследуемого обьекта.
Элементная база – биполярные и полевые транзисторы, интегральные микросхемы, электрические лампы(для увеличения сопротивления до 1013Ом).
Основная статическая характеристика – номинальный коэффициент усиления или номинальный коэффициент передачи, т.е номинальная чувствительность.
Различают усилители переменного и постоянного тока(частотное ограничение по диапазону измерения).
Основные источники погрешностей:
- поводки;
- шумы;
- изменение Uy во времени и под действием влияния факторов.
Погрешность уменьшается за счет введения ООС.
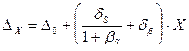 - абсолютная погрешность, приведенная ко входу.
- абсолютная погрешность, приведенная ко входу.
δS – погрешность изменения коэффициента усиления;
δβ – погрешность в цепи ООС
δβ >δS
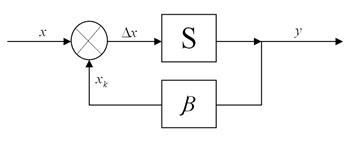
Анализ показывает, что аддитивная составляющая погрешности не уменьшается.
Нестабильность напряжения смещения в УПТ определяется зависимостью параметров усилительных элементов от и прочее. Она вызывает аддитивную погрешность.
Её можно уменьшить путем применения усилителей с модуляцией-демодуляцией (недостаток в том , что они имеют высокую точность при определенном диапазоне усиления сигналов).
Класс точности усилителей переменного тока определяется (не более 4%) мультипликативной погрешностью.
Дата: 2018-11-18, просмотров: 869.
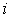
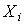 , мм
, мм
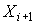 , мм
, мм