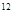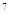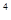Задача 5. Решить уравнение х  - х + х - х+ 1=0.

Решение. Изучая данное уравнение, возможно заметить, что нечетные степени переменной х входят в уравнение с отрицательным знаком. Такое положение может натолкнуть на мысль разбить область решения данного уравнения на области, включая области отрицательных и положительных действительных чисел:

• при х < 0 левая часть уравнения всегда принимает положительные значения, поэтому она не может быть равна нулю. Это значит, что в области отрицательных чисел уравнение решений не имеет.

• область неотрицательных чисел будем рассматривать как два промежутка в отдельности: а) 0 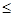 х < 1; б) х = 1; в) х > 1.

а) преобразуем данное уравнение следующим образом:

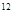х 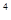 + х  - х 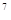 + 1 – х = 0, далее 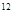х  + х 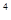(1 - х 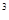) + 1 – х = 0. Тогда при х < 1 левая часть всегда положительна, и поэтому не равна правой части.

б) при х = 1 левая часть уравнения равна 1 .

в) рассматривая уравнение на множестве х >1, также его преобразуем:

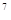х (х 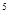 - 1) + х (х  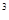- 1) +1 = 0 . Очевидно, левая часть всегда больше 1.

Поскольку во всех трех случаях левая часть не равна 0, то уравнение решений на множестве неотрицательных чисел также не имеет.

3.2 Метод преобразования задачи

Если разбить задачу на несколько подзадач невозможно, то следует попытаться ее как-то преобразовать, но, не меняя язык на котором была задана данная задача. Это значит, что если задача была алгебраической, то преобразованная задача тоже должна быть алгебраической, если она была геометрической то преобразованная задача тоже должна быть геометрической и т.д., поскольку если изменится язык, на котором изложена задача, то это уже будет не преобразование, а моделирование, которое будет рассмотрено ниже.

Задача 6. Решить уравнение х 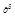 =5. (*)

Данное уравнение не степенное, так как показатель х степени – переменная; и не показательное, так как основание степени – переменная. То есть, имеем дело с уравнением неизвестного вида. Сводим данное уравнение к знакомому виду – показательному, используя подстановку:

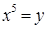 ⇒ (*): х = 5 (**).

Если найдем y из (**), то найдем и х.

,

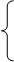
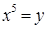х = 5.

Исключим из этой системы х, тогда

,

.

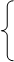
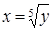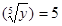Возведем в пятую степень, тогда получим, что 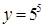. Такое равенство возможно при единственном значении y, а именно y =5, тогда .

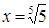Задача 7. Через данную точку А провести прямую таким образом, чтобы ее отрезок с концами на данных прямой и окружности делился точкой А пополам.

Решение. Обозначим искомый отрезок CD, и пусть точка С лежит на окружности, тогда точка D принадлежит прямой m. Поскольку точка А - середина CD, получим, что при центральной симметрии относительно точки

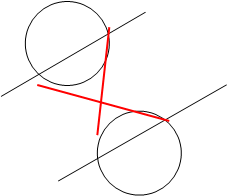Z(m)А точка D перейдет в точку C, и наоборот. aC´ Поэтому данная прямая m и окружность необходимо пересекутся в двух точках или C будут касаться в одной в зависимости от •АD m расположения исходных прямой и окружности. В результате задача сводится к D´m построению образов окружности и прямой при Z(a) центральной симметрии относительно точки А, которые в пересечении с данными прямой m и окружностью a дадут искомые точки C, D, а также C´ и D´. Остается провести требуемую прямую или прямые.

Метод моделирования

Этот метод состоит в замене исходной задачи другой задачей, моделью исходной. Примером использования такого метода является широко применяемый метод решения текстовых (сюжетных) задач путем составления уравнения или системы уравнений. Приведем пример использования этого метода.

Задача 8. В квартире десять лампочек. Сколько существует различных способов освещения квартиры? Два способ освещения считаются различными, если они отличаются состоянием хотя бы одной лампочки. Каждая лампочка может гореть и не гореть. Случай, когда все лампочки не горят, - это тоже способ освещения.

Решение. Чтобы легче подсчитать все различные способы освещения квартиры, изобразим каждую лампочку в виде квадрата, а ее состояние будем отмечать знаком “+”, если лампочка горит, и знаком “ – ” в противоположном случае.

Тогда каждому способу освещения квартиры будет соответствовать строка из десяти квадратов со знаком “+” или “ – ”.

Число же таких строк в таблице и есть искомое число различных способов освещения квартиры

Исходя из выше сказанного, получаем следующую задачу.

Имеем прямоугольную таблицу, содержащую 10 столбцов. В каждой клетке стоит “+” или “ – ”. Любые две строки таблицы отличаются знаками в клеточках, стоящих хотя бы в одном и том же столбце. Какое наибольшее число строк имеет эта таблица?

Если решение этой задачи не очевидно, то можно рассматривать каждую строку таблицы, о которой идет речь в предыдущей задаче, как десятичное число, составленное из цифр 1 и 0 ( 1 ~ “+”, 0 ~ “ – ”). Тогда вопрос задачи будет звучать следующим образом: сколько различных десятизначных чисел можно образовать из цифр 0 и 1? (При этом числа, в записи которых слева стоят одни нули, например, 0100001101 или 0000000001 или даже, 0000000000, также рассматриваются).

Решение. На каждом месте в записи десятизначного числа могут стоять лишь цифры 1 и 0. Поэтому имеется лишь две комбинации цифр на каждом месте. Эти комбинации независимы друг от друга, так как проставление цифры на данном месте в записи числа не зависит от того, какие цифры стоят на других местах. Поэтому общее число комбинаций или возможных десятичных различных чисел равно 2 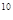 = 1024.

Итак, ответ: общее число способов освещения квартиры равно 1024.

Задача 9. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.

Данная задача легко решается, если построить физическую или векторную ее модели.

Физическая модель. Для построения физической модели нужно вспомнить положения курса физики: 1) центр тяжести двух материальных точек с одинаковой массой лежит в середине отрезка, соединяющего эти точки, с массой, равной сумме масс этих точек;

2) центр тяжести двух материальных точек с различной массой лежит в точке, делящей отрезок в отношении масс (большей массе соответствует меньший отрезок и, наоборот);

3) Центр тяжести системы точек находится путем нахождения центра тяжести пар точек из этой системы, и при этом он не зависит от того , в каком порядке соединяются эти точки попарно.

Решение. Докажем сначала, что медианы треугольника пересекаются в одной точке. Для этого определим центр тяжести системы вершин треугольника. В вершины треугольника – как материальные точки поместим массы по 1 в каждую. Тогда, по 1) положению центр масс каждой пары вершин находится в середине отрезка с концами в этих вершинах.

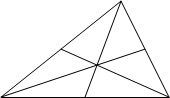Так как 2)середины сторон треугольника – основания медиан, то получаем, что каждая медиана этого треугольника имеет на своих концах массы 1 и 2, считая от вершин треугольника.

3) Пользуясь третьим положением, получим, что точка равновесия каждой медианы имеет массу равную трем. Это говорит о том, что точки равновесия медиан совпадают, то есть медианы пересекаются в одной точке. Используя второе положение, получаем, что данной точкой равновесия каждая медиана делится на два отрезка, которые будут находиться в отношении 2 к 1, считая от вершин треугольника.

Векторная модель. Для доказательства данного утверждения необходимо вспомнить формулу деления отрезка в данном отношении для векторов.

Итак, пусть точка M делит отрезок AB так, что AM=λMB (*), тогда для любой точки О выполнимо следующее векторное соотношение: . . 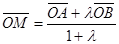, где λ≠ – 1.

Чтобы доказать эту формулу, возьмем векторы 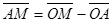 и 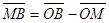. Подставляя эти соотношения в формулу (*), получаем

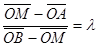, иначе 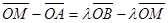. Группируя векторы 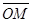, получаем выражение 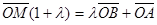. Отсюда

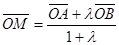, где λ≠ – 1.

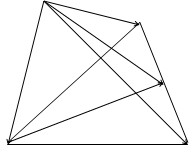
Решение. Выберем произвольную точку О в качестве общего начала векторов.

На медиане А А  возьмем точку G, делящую ее C в отношении 2 : 1, считая от точки А. Тогда на основании формулы деления отрезка в данном отношении будем иметь: 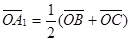 и GА₁

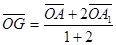.А В

Тогда 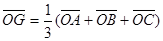 для произвольной точки О.

В это выражение векторы 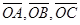входят равноправно, поэтому векторы к точкам, делящих медианы в отношении 2 : 1, будут иметь то же выражение. Это означает, что делящие точки совпадают.