Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется два исходных продукта A и B. Расходы продуктов A и B на 1 т. соответствующих красок и запасы этих продуктов на складе приведены в таблице:
| Исходный | Расход продуктов (в тоннах на 1 т. краски) | Запас продукта на | |
| продукт | краска для внутренних работ | краска для внешних работ | складе ( тонн ) |
| A | 1 | 2 | 3 |
| B | 3 | 1 | 3 |
Продажная цена за 1 тонну краски для внутренних работ составляет 2 000 рублей, краска для наружных работ продается по 1 000 рублей за 1 тонну. Требуется определить какое количество краски каждого вида следует производить предприятию, чтобы получить максимальный доход.
Рассмотрим поэтапное решение этой задачи графическим способом с использованием процедуры « Поиск решения » Excel.
I. Составление математической модели задачи.
1) Переменные задачи.
Обозначим: x1 - количество производимой краски для
внутренних работ;
x2 - соответствующее количество краски
для наружных работ.
2) Ограничения, которым должны удовлетворять переменные задачи:
x1 , x2 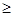 0;
0;
по расходу продукта A: x1 + 2x2 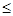 3;
3;
по расходу продукта B: 3x1 + x2 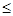 3;
3;
В левых частях последних двух неравенств определены расходы продуктов A и B, а в правых частях неравенств записаны запасы этих продуктов.
3) Целевая функция задачи.
Обозначим Z доход от продажи краски (в тысячах рублей), тогда целевая функция задачи записывается так:
Z = 2x1 + x2 ,
таким образом, задача состоит в том, чтобы найти max Z=2x1+x2 , при ограничениях:
x1 + 2x2 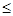 3 (A)
3 (A)
3x1 + x2 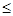 3 (B)
3 (B)
x1 , x2 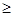 0 .
0 .
Так как переменные задачи x1 и x2 входят в целевую функцию и ограничения задачи линейно, то соответствующая задача оптимизации называется задачей линейного программирования (ЛП)
В рассматриваемом примере содержатся только две переменные x1 и x2, поэтому задачу можно решить графически.
1) На плоскости x1 , x2 строим область допустимых значений переменных, определяемую ограничениями задачи:
x1 + 2x2 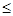 3 (A)
3 (A)
3x1 + 1x2 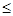 3 (B)
3 (B)
x1 , x2 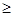 0 .
0 .
Последнее ограничение определяет первый квадрант плоскости. Чтобы построить множество точек удовлетворяющих неравенству (А) нанесем на плоскость график прямой, определяющий границу этого множества: x1+2x2=3 (A).
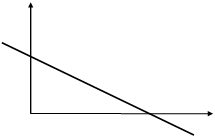
Приведем это уравнение к виду: 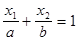 . А это уравнение прямой «в отрезках» и для построения этой прямой используются две точки (a , 0) и (0 , b). (См. рисунок 11).
. А это уравнение прямой «в отрезках» и для построения этой прямой используются две точки (a , 0) и (0 , b). (См. рисунок 11).
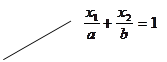
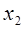
b
a 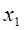
Рис.11.
Проведя уравнение (A) к виду прямой в отрезках, получим:
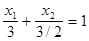
Аналогично, для ограничения (B) уравнение прямой в отрезках будет:
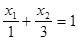
Построим обе прямые на плоскости. Множества точек, удовлетворяющие неравенствам (A) и (B) будут полуплоскости, лежащие под соответствующими прямыми, а множество допустимых значений переменных будет пересечением (общей частью) этих полуплоскостей, лежащее в первом квадранте: четырехугольник ABCD (см. рис.12)

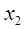
 3
3
2 (B)
 B
B
 C
C



 1 (A)
1 (A)
|
|
|
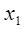
 1 2
1 2
Рис.12.
2) На множестве допустимых решений (ABCD) найдем точку, в которой целевая функция Z=2x1+x2 имеет максимальное значение. Для этого посмотрим линии уровня целевой функции. Линией уровня называется множество точек, на которых функция принимает постоянное значение:
Z = 2x1 + x2 = К ,
где К - задаваемая постоянная.
При К = 1 уравнение линии уровня будет:
2x1 + x2 = 1
или (в отрезках) :
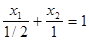
При К = 2, аналогично:
2x1 + x2 = 2 , или 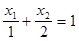 .
.
Нанеся линии уровня на область допустимых решений (рис.13), получим, что при увеличении значения Z соответствующая линия уровня перемещается параллельно предыдущей вправо и вверх. Таким образом, точкой из многоугольника ABCD в которой целевая функция Z имеет максимальное значение будет вершина С. Эта точка и определяет решение задачи.
| |
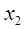

 |
3

|
B
 C
C






 1 (A)
1 (A)

|
|
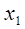
1 2 3
Рис. 13.
3) Вычисление координат оптимальной точки (С).
Точка C лежит на пересечении прямых (A) и (B), поэтому, чтобы определить ее координаты надо решить систему уравнений:
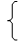 x1 + 2x2 = 3 (A)
x1 + 2x2 = 3 (A)
3x1 + x2 = 3 (B)
Решение:
x1* = 0.6 ; x2* = 1.2 ;
максимальное значение Z:
Z* = 2*0.6 + 1.2 = 2.4.
Вывод
Надстройка Поиск решения в Microsoft Excel даёт возможность найти решение, оптимальное при нескольких входных значениях и наборе ограничений на решение. Программа Поиск решения содержит параметры, управляющие процессом поиска решения: максимальное время, число итераций, точность, допустимое отклонение. Каждый из этих параметров имеет значение по умолчанию, подходящее для большинства задач. Использование новых установок параметров обычно необходимо для проведения серьёзных исследований сложных систем управления. Диспетчер сценариев способен запомнить несколько решений, найденных данным средством, и сгенерировать на этой основе отчёт. Надстройка Поиск решения готовит три вида отчётов, которые характеризуют найденное решение задачи: отчёт по результатам, отчёт по устойчивости и отчёт по пределам. Режим пошагового поиска позволяет наблюдать последовательность приближений к оптимальному решению задачи. Во многих случаях это помогает «почувствовать» сходимость процесса и установить причины неудач и тупиков при поиске оптимального решения. В результате поиска решения EXCEL выводит сообщения о том, удалось ли получить оптимальное решение задачи.
С помощью надстройки Поиск решения можно решать как линейные задачи (задачи линейного, целочисленного и стохастического программирования), так и нелинейные (задачи нелинейного программирования), а также системы нелинейных уравнений. Для успешной работы средства Поиск решения следует стремиться к тому, чтобы зависимости были гладкими или, по крайней мере, непрерывными.
Поиск решения можно использовать и для решения задач математического программирования других типов, но в этом случае процедура поиска часто заканчивается неудачей, а при благоприятном исходе находит лишь один из локальных оптимумов. Поэтому решение таких задач с помощью данной процедуры следует предварять их аналитическим исследованием на предмет свойств области допустимых решений, чтобы выбрать подходящие начальные значения и сделать правильное заключение о качестве и практической применимости полученного решения.
Список литературы
1. Л. В. Рудикова «Microsoft Excel для студента», Санкт – Петербург, БХВ-Петербург, 2005;
2. «Лабораторные работы на персональном компьютере» И. Ф. Цисарь, издательство «Экзамен», Москва, 2002;
3. Додж М. и др. «Эффективная работа с Microsoft Excel», 2000.СПб.:Питер, 2001.
4. Солодовников А. С. «Введение в линейную алгебру и линейное программирование». Москва, издательство «Просвещение», 1966. – 184 с.
5. Стрейвер А. «Теория линейного и целочисленного программирования» в двух томах, том 1: перевод с английского. – Москва: Мир, 1991. – 360 с.
6. Ашманов С.А.«Линейное программирование». - М.: Наука, 1981.
7. Банди Б. «Основы линейного программирования»: Пер. с англ. - М.: Радио и связь, 1989.
8. Кораблин М. А. «Информатика поиска управленческих решений», Москва, СОЛОН-Пресс, 2003.
9. Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.1. Общие задачи, Минск, Изд-во БГУ им. В.И. Ленина, 1977. - 176 с.
Дата: 2019-12-10, просмотров: 328.