Типовые входные воздействия
Одним из видов связи СУ с внешней средой является связь формирования задающего воздействия. В некоторых случаях, например в следящих системах, это воздействие заранее не определено и может быть любым.
Для сравнительной оценки реакции разных систем на входное управляющее воздействие используют типовые функции времени
1) ступенчатое единичное воздействие.
 |
x(t) x(t)=[1];
 1
1
 0 t
0 t
Если уровень входного воздействия отличен от 1, то x(t)=U0[1] – ступенчатое воздействие
 | |||
 | |||
X(t)= 0, t<0;
 X(t) U0, t ³ 0;
X(t) U0, t ³ 0;
U0
 t
t
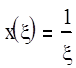 ;
; 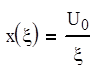
Данное воздействие используется при оценке качества процесса регулирования.
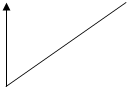
2) Линейное воздействие
 | |||
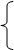 | |||
X(t) x(t) = 0, t£0; x(x)=k/x2
Kt, t>0;
 t
t
3) степенное воздействие
 |
 x(t)
x(t)
 x(t) x(t) = 0, t<0
x(t) x(t) = 0, t<0
x0+x1t+ x2t2+…+, t ³ 0,

t
Если 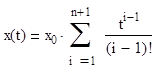 , то
, то 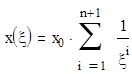
Эти воздействия используются для оценки точности систем регулирования.
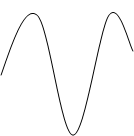
4) гармоническое воздействие постоянной амплитуды
 x(t)
x(t)
 x0
x0
 | |||
 | |||
t x(t) = 0, t<0,
x0 sinwt, t ³ 0
 -x0
-x0
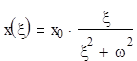
используется для оценки частных свойств.
5) эксионенциальное
 x(t)
x(t)

 x0
x0
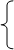
x(t) = 0, t<0;
 t x0 e – jt, t ³ 0
t x0 e – jt, t ³ 0
Используется для оценки точности системы регулирования.
6) импульсное воздействие
 |
d(t) I = F tg = mv = const
V= I/m
Dt ® 0 ; A ®¥ x®1
 t
t
 |
d
 t
t
Введение импульсного воздействия позволяет при исследовании свойств СУ представлять любые воздействия в виде последовательности единичных мгновенных импульсов. Важное значение имеет d - функция.
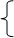 Импульсной d - функцией называется функция, равная нулю всюду, кроме начала координат и принимающая там ¥ большое значение, т.е. d(t) = 0, t=0
Импульсной d - функцией называется функция, равная нулю всюду, кроме начала координат и принимающая там ¥ большое значение, т.е. d(t) = 0, t=0
¥, t=0
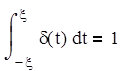 , при x¹0
, при x¹0
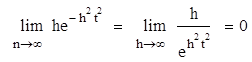
Основные свойства дельта функции.
1. Свойство четности
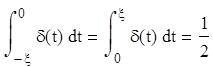 , при x >0
, при x >0
2. Для любой непрерывной функции x ( t ) справедливо
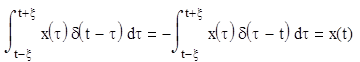
Возмущающие воздействия
1. Сброс нагрузки
f(t)= f1, 0 £ t £ t1
f2, t > t1, при f2=0,
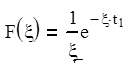
2. Наброс нагрузки
f(t)= f2, t £ 0 £ t1
f1, t > t1
3. Периодическое треугольное
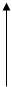 f(t)
f(t)




 f1
f1



 t
t
t
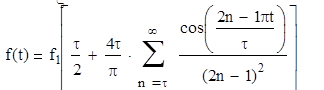
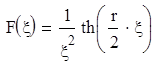
4. Периодическое параболическое
 f(t)
f(t)

 f1
f1
 t
t
n – номер гармоники разложения периодической функции в ряд Фурье.
5. Ступенчатое
 f(t)
f(t)






 f1
f1
 t 2t 3t t
t 2t 3t t

 -f1
-f1
6. Гармоническое
 |

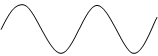 f1
f1

 t
t
 - f1
- f1
 t
t
Структурные схемы объектов и систем.
Структурные схемы САУ отражают их состав и связи между образующими систему элементами, т.е. они отражают причинно – следственные взаимосвязи и последовательность преобразования информации (сигналов) в СУ.
Графически структурные схемы представляются в виде направленных связей динамических звеньев. При этом любой элемент системы представляется в виде пары «вход-выход», а динамические свойства устанавливаются оператором – передаточной функцией. Таким образом в классе линейных систем любой элемент на структурной схеме имеет вид х – вход, у – выход, w(s) – оператор
|

 Х У
Х У
В общем случае используются следующие обозначения:
|

 Х У - динамическое звено
Х У - динамическое звено

 Х x Х x - Х + У - сумматор
Х x Х x - Х + У - сумматор



 ;
;
У У
®; Þ - Лини связи

 Х x x = Х – У
Х x x = Х – У



 ;
;
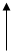 - сравнивающий элемент
- сравнивающий элемент
У У
 |
Х Z = Х·У
- 
 блок перемножения
блок перемножения
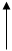 У
У

 Х Z = Х / У
Х Z = Х / У
 |  |
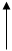 - блок деления
- блок деления
У




|





 Или - нелинейный
Или - нелинейный
элемент
|

 - эквивалентный элемент
- эквивалентный элемент
2. Преобразование структурных схем
Последовательное соединение звеньев.
|
|


 Х1(x ) У1 (x )
Х1(x ) У1 (x )
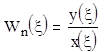
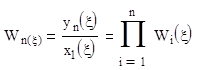
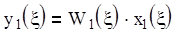
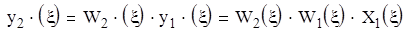

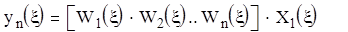
Таким образом передаточная функция последовательно соединенных звеньев равна произведению всех передаточных функций.
Параллельно – согласное соединение звеньев
|
 |  |  | |||||
 | |||||||


|
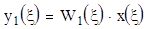
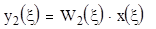
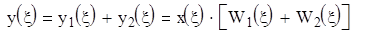 Þ
Þ
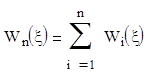
Т.е. при таком соединении звеньев передаточная функция системы равна алгебраической сумме всех передаточных функций.
Параллельно – встречное соединение звеньев
|
 X(x) E(x) Y(x)
X(x) E(x) Y(x)
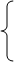



 Y(x)=E(x)×W1(x)
Y(x)=E(x)×W1(x)
 1 случай X1(x)=y(x)×W2(x)
1 случай X1(x)=y(x)×W2(x)
|
 | |||
 | |||
Wкд=?
 X(x) E(x)
X(x) E(x)



|
|


 Y(x)
Y(x)
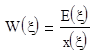
Wкд(x) – передаточная функция по каналу передачи управляющего воздействия.
Wзс(x) – передаточная функция замкнутой системы по отклонению или ошибке в канале передачи управляющего воздействия.
E(x)=x(x)±y(x)×W2(x)
Y(x)=W1(x)×[x(x)±y(x)×W2(x)]
Y(x)[1± W2(x)×A]= W1(x)×x(x)
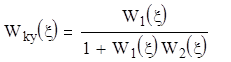
Передаточная функция заданной системы равна передаточной функции прямого канала деленной на единицу плюс (отрицательная обратная связь) или минус (положительная обратная связь) произведение передаточных функций прямого канала и канала обратной связи.
Положительная обратная связь – связь алгебраически суммируемая с сигналом задания, т.е. увеличение сигнала обратной связи приводит к увеличению сигнала на выходе элемента сравнения.
Отрицательная обратная связь – связь, при которой ее возрастание приводит к уменьшению сигнала на выходе элемента сравнения, т.е. сигналы задания и обратной связи вычитаются.
Для линейных систем используется только отрицательная обратная связь.
2 случай: выход системы ошибок;
E(x)=x(x)±Е(x)×W1(x)×W2(x);
(1± W1(x)×W2(x))=x(x);
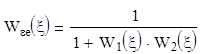
При наличии жесткой обратной связи вид передаточной функции по каналу ошибки не изменяется, а в передаточной функции по каналу передачи управляющего воздействия в прямом канале появляется составляющая бывшей обратной связи.
Перенос линии связи
|
|





 У Х
У Х
=
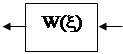 | |||||||||
 | |||||||||
|
| ||||||||
Х У Х У





 =
=
 | |||||||||||||
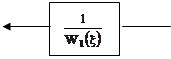 | |||||||||||||
|  |  |
| ||||||||||





 Х У U = Х Х1 U
Х У U = Х Х1 U
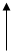
 Z Х2
Z Х2
|
 | |||
 | |||

|
|
 X Z Х1 Z
X Z Х1 Z





 =
=
|
 | |||
 | |||
Типовые входные воздействия
Одним из видов связи СУ с внешней средой является связь формирования задающего воздействия. В некоторых случаях, например в следящих системах, это воздействие заранее не определено и может быть любым.
Для сравнительной оценки реакции разных систем на входное управляющее воздействие используют типовые функции времени
1) ступенчатое единичное воздействие.
 |
x(t) x(t)=[1];
 1
1
 0 t
0 t
Если уровень входного воздействия отличен от 1, то x(t)=U0[1] – ступенчатое воздействие
 | |||
 | |||
X(t)= 0, t<0;
 X(t) U0, t ³ 0;
X(t) U0, t ³ 0;
U0
 t
t
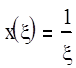 ;
; 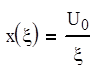
Данное воздействие используется при оценке качества процесса регулирования.
2) Линейное воздействие
 | |||
 | |||
X(t) x(t) = 0, t£0; x(x)=k/x2
Kt, t>0;
 t
t
3) степенное воздействие
 |
 x(t)
x(t)
 x(t) x(t) = 0, t<0
x(t) x(t) = 0, t<0
x0+x1t+ x2t2+…+, t ³ 0,

t
Если 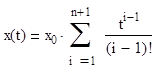 , то
, то 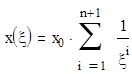
Эти воздействия используются для оценки точности систем регулирования.
4) гармоническое воздействие постоянной амплитуды
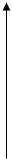
 x(t)
x(t)
 x0
x0
 | |||
 | |||
t x(t) = 0, t<0,
x0 sinwt, t ³ 0
 -x0
-x0
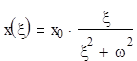
используется для оценки частных свойств.
5) эксионенциальное
 x(t)
x(t)

 x0
x0
x(t) = 0, t<0;
 t x0 e – jt, t ³ 0
t x0 e – jt, t ³ 0
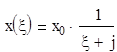
Используется для оценки точности системы регулирования.
6) импульсное воздействие
 |
d(t) I = F tg = mv = const
V= I/m
Dt ® 0 ; A ®¥ x®1
 t
t
 |
d

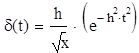
 t
t
Введение импульсного воздействия позволяет при исследовании свойств СУ представлять любые воздействия в виде последовательности единичных мгновенных импульсов. Важное значение имеет d - функция.
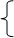 Импульсной d - функцией называется функция, равная нулю всюду, кроме начала координат и принимающая там ¥ большое значение, т.е. d(t) = 0, t=0
Импульсной d - функцией называется функция, равная нулю всюду, кроме начала координат и принимающая там ¥ большое значение, т.е. d(t) = 0, t=0
¥, t=0
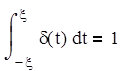 , при x¹0
, при x¹0
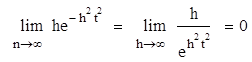
Основные свойства дельта функции.
1. Свойство четности
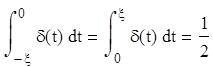 , при x >0
, при x >0
2. Для любой непрерывной функции x ( t ) справедливо
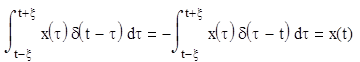
Возмущающие воздействия
1. Сброс нагрузки
f(t)= f1, 0 £ t £ t1
f2, t > t1, при f2=0,
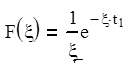
2. Наброс нагрузки
f(t)= f2, t £ 0 £ t1
f1, t > t1
3. Периодическое треугольное
 f(t)
f(t)




 f1
f1



 t
t
t
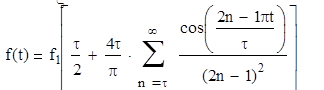
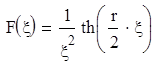
4. Периодическое параболическое
 f(t)
f(t)

 f1
f1
 t
t
n – номер гармоники разложения периодической функции в ряд Фурье.
5. Ступенчатое
 f(t)
f(t)






 f1
f1
 t 2t 3t t
t 2t 3t t

 -f1
-f1
6. Гармоническое
 |

 f1
f1

 t
t
 - f1
- f1
 t
t
Дата: 2019-12-09, просмотров: 272.