Совершенно очевидно, что двоичное число представляется последовательностью нулей и единиц – разрядов. Как и в любой позиционной системе, каждому разряду присвоен определенный вес – показатель степени основания системы. Веса первых 10 позиций представлены в таблице.

 Веса первых десяти позиций двоичной системы счисления

Позиция	9	8	7	6	5	4	3	2	1	0
Вес	512	256	128	64	32	16	8	4	2	1
Образование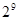

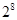
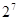
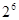
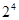
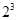
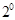
В двоичной системе счисления даже сравнительно небольшие числа занимают много позиций.

Как и в десятичной системе, в двоичной системе счисления для отделения дробной части используется точка (двоичная точка). Каждая позиция слева от этой точки также имеет свой вес – вес разряда дробной части числа. Значение веса в этом случае равно основанию системы счисления (т.е. двойке), возведенному в отрицательную степень.

Получить десятичное число из двоичного чрезвычайно просто. Согласно формуле

для двоичной системы счисления получаем:

Пример иллюстрирует процесс получения десятичного числа из двоичного.

    Перевод двоичного числа  в десятичное

4.2 Преобразование десятичных чисел в двоичные

Перевод из двоичной системы в десятичную несколько сложнее. Рассмотрим несколько алгоритмов.

Метод деления

Другим методом является так называемый метод деления. Он применяется для преобразования целых чисел. Ниже приведен его алгоритм.

Разделим нацело десятичное число на двойку. Если есть остаток, запишем в младший разряд единицу, а если нет – нуль и снова разделим результат от первого деления. Повторим процедуру так до тех пор, пока окончательный результат не обнулиться.

Пример 4.3 Перевод десятичного числа 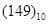 в двоичное методом деления

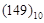
	2
148	–74	2
1	74	–37	2
	0	36	–18	2
		1	18	–9	2
			0	8	–4	2
				1	4	–2	2
					0	2	–1	2
						0	0	0
							1		старший разряд
(10010101)2=(149)10				ответ

Метод умножения

И, наконец, метод умножения. Метод применяется для преобразования десятичных дробей (чисел меньших единицы).

Число умножается на 2, если результат ³ 1, то в старший разряд записывается единица, если нет, то нуль. Умножаем на 2 дробную часть результата и повторяем процедуру. И так далее до получения нужной степени точности или до обнуления результата.

Перевод десятичного числа 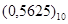 в двоичное методом умножения

Постановка задачи.

Наиболее часто встречающиеся системы счисления это двоичная, десятеричная и шестнадцатеричная система счисления, восьмеричная система счисления встречается только в инженерных калькуляторах, практическое же применения её давно прекратилось. Итак, наша задача осуществить перевод целых чисел из одной системы счисления в другую. Для этого выберем двоичную, восьмеричную, десятеричную и шестнадцатеричную систему счисления.