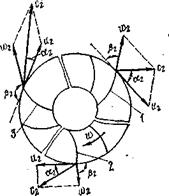
В центробежных насоса можно применять лопатки трёх видов по кривизне относительно направления вращения колеса:

1. загнутые назад;

2. загнутые радиально;

3. загнутые вперёд

R₁, R₂, n = const

u₂ =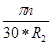  

При одинаковых оборотах и размерах колёс, загнутые вперёд лопатки сообщают наибольшую абсолютную скорость, поэтому наибольший теоретический напор дают лопатки, загнутые вперёд. Однако, если скорость жидкости на выходе из насоса большая, то увеличиваются гидравлические потери пропорционально квадрату скорости. Поэтому колёса с загнутыми вперёд лопатками имеют более низкий к.п.д., чем при лопатках, загнутых назад.

Кроме того, каналы между лопатками загнутыми назад более плавно расширяются, чем при лопатках загнутых вперёд. Поэтому для насосов всегда применяют колёса с загнутыми назад лопатками, т.к. они обеспечивают наибольший к.п.д. насоса.

ДАВЛЕНИЕ НАСОСА, ОПРЕДЕЛЯЕМОЕ ПО ПОКАЗАНИЯМ ПРИБОРОВ

Насос по отношению к уровню жидкости может быть установлен двумя способами:

1 насос находится над уровнем жидкости водоёма

                                                            М

                           В

Напор насоса определяется по формуле:

Н_н = 10Рм+10Рв+ 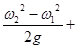z_м.в. [м],

где: Р_м, Р_в показания манометра и вакуумметра в кгс/см² ;

ω₂,ω₁ – скорость жидкости на выходе и входе насоса;

    Z_м.б. – расстояние между отметками манометра и вакуумметра .

 2 Насос находится «под заливом», т.е. с избыточным давлением на всасывании

                                                                                        М₂

                           М₁

     Н_н = 10Рм₂ – 10Рм₁ +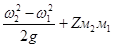  

    Z_м.2м1 – расстояние между отметками манометров;  

    Р_м1, Р_м2 –показания манометров.

ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ

Соотношение, описывающее зависимость расхода напора и мощности от числа оборотов называется законом пропорциональности.

n₁ – ν₁, W₁, u₁

n₂ – ν₂, W₂, u₂

n₂>n₁

u = ωR =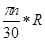   

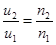
Q = Fω

Подача насоса изменяется пропорционально радиальной составляющей скорости на выходе.

Q = Fν_2nη₀

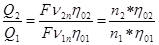
Объёмный к.п.д. (η₀) остаётся практически неизменным при изменении числа оборотов в пределах 50%.

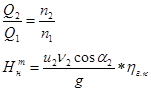
Из этой формулы видно, что u_2, ν₂ каждый из которых зависит от числа оборотов

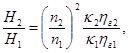 где κ₂ и η_г при изменении числа оборотов в пределах 50% остаются неизменными, поэтому формула принимает виды:

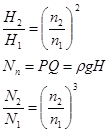
ЗАКОН ПОДОБИЯ

При конструировании и эксплуатации центробежных насосов пользуются законами их подобия и в первую очередь подобием рабочих колёс этих насосов. Различают геометрическое и кинематическое подобие рабочих колёс.

Геометрическое подобие означает пропорциональность соответствующих размеров их проточной части (d, ширины лопаток, радиусов кривизны лопаток и т.д.)

Кинематическое подобие предопределяет одинаковое направление векторов скорости в сходственных точках потока.

Если геометрическое подобие колеса d₂ и d₁ вращаются с одинаковым числом оборотов, то получают следующие зависимости.

Подача пропорциональна площади выходного сечения рабочего колеса и радиальной составляющей скорости на выходе. Если рабочие колёса подобны, то площадь выходного сечения пропорциональна d², а скорость на выходе пропорциональна d, поэтому:

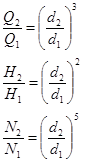
Коэффициент быстроходности – число оборотов в одну минуту рабочего колеса, которая геометрически подобна рассматриваемому колесу и при подачи жидкости Q = 75 л/сек обеспечивает напор Н = 1м.

n_s = 3,65  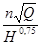, где n – число оборотов в 1 мин.
  Q [м³/с]

Примечание: для насосов с двухсторонним подводом жидкости на рабочее колесо в формулу подставляется Q/2.

n_s=50 – 80 насосы тихоходные;

n_s= 80 – 150   насосы нормальной быстроходности;

n_s= 150 – 300 насосы быстроходные.

При увеличении быстроходности уменьшается величина отношения диаметра рабочего колес к диаметру входа на рабочее колесо с3-2,5 (тихоходные) до 1,8 – 1,4 (быстроходные).

   n_s ↑ -  Q↑ H↓

    n_s↓ - Q↓ H↑