Конкуренция в условиях рынка часто выражается в том, чтобы получить заказ. Для этого надо быть конкурентно-способным. При обосновании инвестиционных проектов, разработка годовых (квартальных) программ, планировании хозяйственной деятельности требуется информация о прогнозном коэффициенте (индексе). При современных условиях, которые складываются на рынке, это стало необходимым. Чтобы выжить в условиях конкуренции и появлении новых фирм различной деятельности поможет нам метод простой средней величины. Средние величины исчисляются очень часто. Применяются степенные и структурные средние. К степенным относятся следующие виды: арифметическая, гармоническая, хронологическая, геометрическая. Наиболее распространена средняя арифметическая.

Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Метод средних величин заключается в замене индивидуальных значений варьирующего признака единиц наблюдения, т.е. в замене x₁, x₂, x₃, ... x_n некоторой уравненной величиной .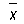

Средние величины применяются для оценки достигнутого уровня изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности предприятий (объединений), фирм, банков и других хозяйственных единиц; средние используются при выявлении взаимосвязей явлений, при прогнозировании, а также расчете нормативов. Средняя величина всегда именованная, имеет ту же размерность (единицу измерения), что и признак у отдельных единиц совокупности.

Основным условием научного использования средней величины является качественная однородность совокупности, по которой исчислена средняя. Поэтому очень важное правило - вычислять средние величины лишь по однородной совокупности единиц. Только при выполнении этого условия средняя как обобщающая характеристика отражает общее, типичное, закономерное, присущее всем единицам исследуемой совокупности. Прежде чем вычислять средние величины, необходимо произвести группировку единиц исследуемой совокупности, выделив качественно однородные группы.

Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, - групповыми средними .

Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.

Средняя арифметическая простая и взвешенная. Если имеется несколько различных индивидуальных величин одного и того же вида и надо исчислить среднюю, то необходимо найти сумму всех индивидуальных величин и поделить полученную сумму на их число. Обозначим индивидуальные значения признака через x1, x2, x3, ...xn, число индивидуальных величин - n, среднюю величину - .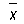

Средняя величина, вычисленная по формуле:

;

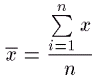х – значение осредняемого признака (инфляция)

n – число единиц совокупности (месяцы)

называется средней арифметической простой.

Средняя арифметическая простая равна частному от деления суммы индивидуальных значений признака на их количество.

Пример. Требуется вычислить средний стаж работы 12 работников туристической фирмы. При этом известны индивидуальные значения признака (стажа) в годах: 6, 4, 5, 4, 3, 3, 5, 6, 3, 7, 4, 5.

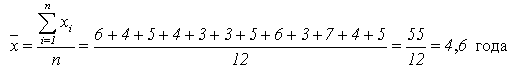
Как видим, средняя арифметическая может оказаться дробным числом, если даже индивидуальные значения признака заданы только целыми числами. Это вытекает из сущности средней арифметической, которая есть величина абстрактная (теоретическая), т.е. она может принимать такое числовое значение, которое не встречается в представленной совокупности индивидуальных значений признака.

Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности.

Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается один (или одинаковое число) раз. Другими словами, средняя арифметическая простая рассчитывается по группировочным единицам совокупности.

Расчет новой стоимости

Зная средний коэффициент инфляции за год,

9%/12мес=0,75%=0,0075

мы можем посчитать новую стоимость одной струны.

Новая стоимость одной струны

1 месяц 109 руб.*0,0075=0,82 руб.

           109 руб.+0,82 руб.=109,82 руб.

или

           109 руб.*1,0075=109,82 руб. 

2 месяц 109,82 руб.*1,0075=110,64 руб.

3 месяц 110,64 руб.*1,0075=111,47 руб.

4 месяц 111,47 руб.*1,0075=112,31 руб.

5 месяц 112,31 руб.*1,0075=113,15 руб.

6 месяц 113,15 руб.*1,0075=114,00 руб.

7 месяц 114,00 руб.*1,0075=114,86 руб.

8 месяц 114,86 руб.*1,0075=115,72 руб.

9 месяц 115,72 руб.*1,0075=116,59 руб.

10 месяц 116,59 руб.*1,0075=117,46 руб.

11 месяц 117,46 руб.*1,0075=118,34 руб.

12 месяц 118,34 руб.*1,0075=119,23 руб.