Побудова моделі Квазі-Шарпа

Модель Квазі-Шарпа відноситься до оптимізаційних моделей і тому для неї характерні певні особливості, які притаманні всім моделям, які відносяться до «портфельної теорії». Розглянемо загальні засади цієї моделі.

Нехай доходність портфелю з N цінних паперів R_p та його ризикованість s_p визначається функціями:

Rp = RETURN (Wi, si, ri; i = 1K N);                                             (2.1)

sp = RISK (WI, si, ri; i = 1K N),                                                    (2.2)

де W_i — процентна частка цінних паперів портфеля;

s_i — деяка характеристика ризику даного цінного паперу, звичайно це середнє квадратичне відхилення доходності цінних паперів;

r_i — доходність цінних паперів.

При розв'язуванні задачі необхідно урахувати наступні натуральні обмеження:

­ сума усіх акцій (у відсотках) складає 100%:

W1+W2+K+Wi+K+Wn = 1 (2.3)

­ кількість акцій не може бути від'ємною (W_I = 0)

Розв'язуванням задачі є певна цільова структура портфеля, представлена набором значень (W₁, W₂,..., W_N). Ідеальна постановка задачі оптимізації портфеля — отримати максимальну доходність при мінімальному ризику:

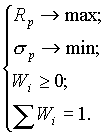                     (2.4)

Але така задача некоректна, тобто не має однозначного рішення. Ідеальний результат недосяжний, як і все ідеальне.

Виходом з положення є введення критичних обмежень.

Перший варіант — задатися певною максимально допустимою величиною ризику s_req Тоді задача оптимізації зводиться до вибору такої структури портфеля, при якій ризик портфеля не перевищує заданого значення, а доходність портфеля є максимальною. Така задача надалі буде називатися прямою задачею:

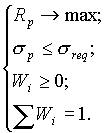                     (2.5)

Другий варіант — задається певною мінімально допустимою величиною доходності. В цьому випадку задача оптимізації зводиться до вибору такої структури портфеля, прибуток якого вищий або ж дорівнює заданому значенню, а ризик мінімальний:

                     (2.6)

Розв'язавши пряму і обернену задачі з оптимізації портфеля з N цінних паперів підприємство отримає дані — скільки та які цінні папери необхідно придбати, щоб сформувати портфель, який (по міркам підприємства) має достатньо високу доходність при допустимому ризику

За моделлю Квазі-Шарп доходність цінного папера пов'язується з доходністю одиничного портфеля функцією лінійної регресії вигляду:

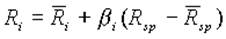(2.7)

де R_i — доходність цінного паперу;

R_sp — доходність одиничного портфеля;

b_і — коефіцієнт регресії;

¯R — середня доходністъ цінного папера за минулі періоди;

¯R_sp — середня доходність одиничного портфеля за минулі періоди.

Коефіціент b характсризує ступінь залежності доходності цінного папера від доходності одиничного портфеля. Чим вищий b, тим сильніше залежить доходність цінного папера від коливань доходності одиничного портфеля, тобто від коливань доходності решти цінних паперів, що входять в одиничний портфель. Коефіцієнт b називають b-ризиком, але його трактування має відміну від трактування однойменного показника в моделі Шарпа.

При практичному застосуванні моделі Квазі-Шарп для оптимізації фондового портфеля використовуються наступні формули.

За доходність одиничного портфеля у період t береться середнє значення доходності цінних паперів, що його складають, за цей же період:

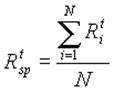                    (2.8)

де R_spt — доходність одиничного портфеля в період t

R_it — доходність i-го цінного папера за період t.

Середня доходність цінного папера за минулі періоди:

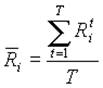                      (2.9)

де R_it — доходність цінного папера за період t,

T — кількість періодів часу, що розглядається.

Середня доходність одиничного портфеля за минулі періоди:

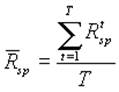                  (2.10)

Коефіцієнт b цінного папера розраховується за формулою:

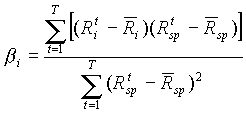                                                 (2.11)

Залишковий ризик цінного паперу:

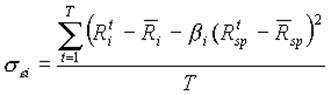                                   (2.12)

Ризикованість одиничного портфеля:

(2.13)

В розглянутій моделі є зовнішня змінна – норма доходності цінних паперів емітента за кожен із періодів. До контрольованих змінних слід віднести:

­ склад портфелю цінних паперів;

­ норма ризику портфелю;

­ норма доходності всього портфелю;

­ максимальна частка цінних паперів кожного з емітентів у портфелі.

Прикладом неконтрольованих змінних можуть служити стан законодавства, політична стабільність.

Змінні управління залежать від того, який тип задачі буде вирішуватись: пряма чи зворотна. При розв’язанні прямої задачі змінною управління є бажаний рівень доходності портфелю цінних паперів. Тобто змінюючи його, можна знайти оптимальний набір, який задовольняє заданому рівню доходності.

При розв’язанні зворотної задачі змінною управління є максимальний рівень ризику, який стає своєрідним обмеженням при розв’язанні задачі оптимізації.

Розробка програмного засобу передбачає реалізацію лінійного алгоритму на основі наведеної нижче блок-схеми (рисунок 2.1).

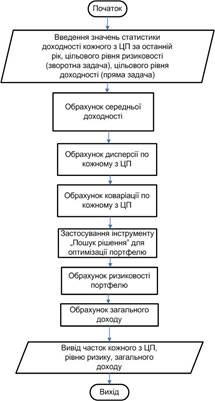
Рисунок 2.1 – Блок-схема алгоритму вирішення задачі оптимізації портфелю цінних паперів

Інформаційна модель задачі

Розглянемо інформаційну модель задачі, яку розділено на такі основні підсистеми:

­ підсистема вхідної інформації;

­ підсистема обробки;

­ підсистема виводу інформації.

Схематично модель вирішення прямої задачі оптимізації портфеля цінних паперів можна зобразити у наступному вигляді (рисунок 2.2):

Для вирішення зворотної задачі оптимізації портфеля цінних паперів інформаційна модель буде мати дещо інший вигляд (рисунок 2.3):

Інформаційне забезпечення моделі має своєю основою статистичну інформацію про стан фондового ринку цінних паперів України, яка доступна на сайті компанії «Foyil». Головна перевага Foyil Securities – акцент на аналітичні дослідження щодо кожного емітенту, цінні папери якого рекомендуються клієнтам. Аналітичний відділ Foyil Securities проводить усебічні дослідження українських публічних компаній[7].