Вариант № 1
Найти частные производные данной функции по каждой из независимых переменных x и y .
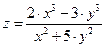
2. Найти производные сложных функций по каждой из независимых переменных.
2.1 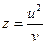 , где
, где 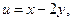
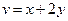
2.2 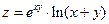 , где
, где  ,
, 
3.Вычислить приближенно, заменяя приращение функции дифференциалом  .
.
4. Найти производные от функций, заданных неявно: 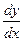 для
для  и
и 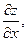
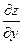 для
для 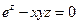 .
.
5. Найти 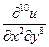 , если
, если 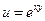 .
.
6. Исследовать на максимум и минимум функцию 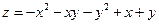 .
.
7. Найти наибольшее и наименьшее значения функции
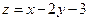 , в области
, в области 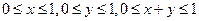 .
.
8. Найти условные экстремумы функции 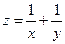 при
при 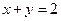 .
.
9. Для данной поверхности 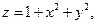 составить уравнения касательной плоскости и нормали в точке M(1,1,?).
составить уравнения касательной плоскости и нормали в точке M(1,1,?).
Вариант № 2
Найти частные производные данной функции по каждой из независимых переменных x и y .
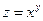
2. Найти производные сложных функций по каждой из независимых переменных.
2.1 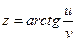 , где
, где 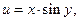
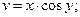
2.2 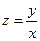 , где
, где  ,
, 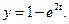
3.Вычислить приближенно, заменяя приращение функции дифференциалом 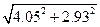 .
.
4. Найти производные от функций, заданных неявно: 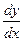 для
для 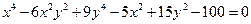 : и
: и 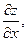
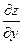 для
для  .
.
5. Найти 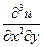 и
и 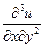 , если
, если  .
.
6. Исследовать на максимум и минимум функцию 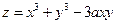 .
.
7. Найти наибольшее и наименьшее значения функции
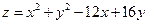 , в области
, в области  .
.
8. Найти условные экстремумы функции 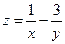 при
при 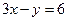 .
.
9. Для данной поверхности 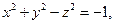 составить уравнения касательной плоскости и нормали в точке M(2,2,3).
составить уравнения касательной плоскости и нормали в точке M(2,2,3).
Вариант №3
Найти частные производные данной функции по каждой из независимых переменных x и y .
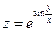
2. Найти производные сложных функций по каждой из независимых переменных.
2.1  , где
, где 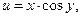
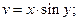
2.2 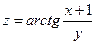 , где
, где 
3.Вычислить приближенно, заменяя приращение функции дифференциалом 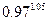 .
.
4. Найти производные от функций, заданных неявно: 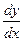 для
для 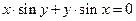 : и
: и 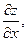
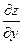 для
для 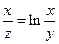 .
.
5. Найти  , если
, если  .
.
6. Исследовать на максимум и минимум функцию 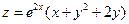 .
.
7. Найти наибольшее и наименьшее значения функции
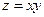 , в области
, в области  .
.
8. Найти условные экстремумы функции 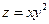 при
при 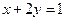 .
.
9. Для данной поверхности 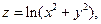 составить уравнения касательной плоскости и нормали в точке M(1,0,?).
составить уравнения касательной плоскости и нормали в точке M(1,0,?).
Вариант №4
Найти частные производные данной функции по каждой из независимых переменных x и y .
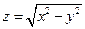
2. Найти производные сложных функций по каждой из независимых переменных.
2.1 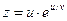 , где
, где 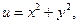
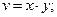
2.2 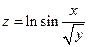 , где
, где 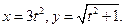
3.Вычислить приближенно, заменяя приращение функции дифференциалом  .
.
4. Найти производные от функций, заданных неявно: 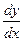 для
для 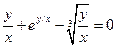 : и
: и 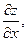
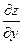 для
для 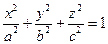 .
.
5. Найти 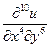 , если
, если 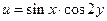 .
.
6. Исследовать на максимум и минимум функцию 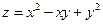 .
.
7. Найти наибольшее и наименьшее значения функции
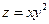 , в области
, в области  .
.
8. Найти условные экстремумы функции 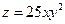 при
при 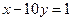 .
.
9. Для данной поверхности  составить уравнения касательной плоскости и нормали в точке M(
составить уравнения касательной плоскости и нормали в точке M( 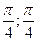 ,?).
,?).
Вариант №5
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Вариант №10
Вариант №11
Вариант №12
Вариант №13
Вариант №14
Вариант №15
Вариант №16
Вариант №17
Вариант №18
Вариант №19
Вариант №20
Вариант №21
Вариант №22
Вариант №23
Вариант №24
Вариант №25
Вариант № 1
Найти частные производные данной функции по каждой из независимых переменных x и y .
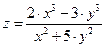
2. Найти производные сложных функций по каждой из независимых переменных.
2.1 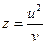 , где
, где 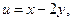
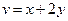
2.2 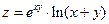 , где
, где  ,
, 
3.Вычислить приближенно, заменяя приращение функции дифференциалом  .
.
4. Найти производные от функций, заданных неявно: 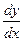 для
для  и
и 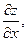
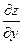 для
для 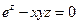 .
.
5. Найти 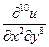 , если
, если 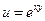 .
.
6. Исследовать на максимум и минимум функцию 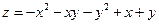 .
.
7. Найти наибольшее и наименьшее значения функции
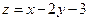 , в области
, в области 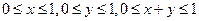 .
.
8. Найти условные экстремумы функции 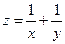 при
при 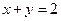 .
.
9. Для данной поверхности 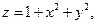 составить уравнения касательной плоскости и нормали в точке M(1,1,?).
составить уравнения касательной плоскости и нормали в точке M(1,1,?).
Вариант № 2
Дата: 2019-12-10, просмотров: 326.