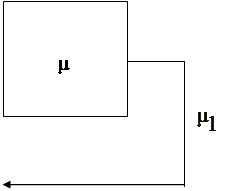
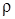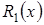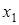Исследуем сеть связи, функционирование которой изложено в разделе 1, в условиях большой задержки. В этом случае удобнее рассматривать случай, когда интенсивность каждой заявки в ИПВ равна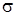 
. Структура такой СМО имеет вид рис. 3.1.
 |  | |||||||||||
 |  | |||||||||||
 |  | |||||||||||
 | ||||||||||||
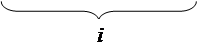Рис. 3.1 – Модель системы массового обслуживания
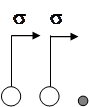
Вероятности переходов из состояния системы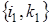 
в произвольный момент времени t в состояние 
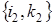за бесконечно малый интервал времени 
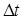показаны на рис. 3.2, рис. 3.3, рис. 3.4.
Выпишем уравнения статистического равновесия для нестационарного распределения процесса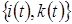 
, описывающего функционирование сети
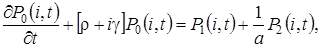
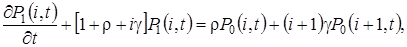(3.1)
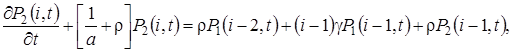
где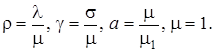 
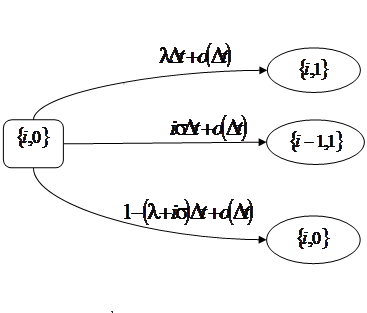
Рис. 3.2 – Возможные переходы из состояния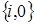 
 |
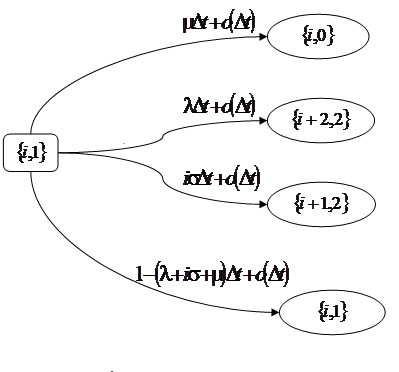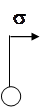
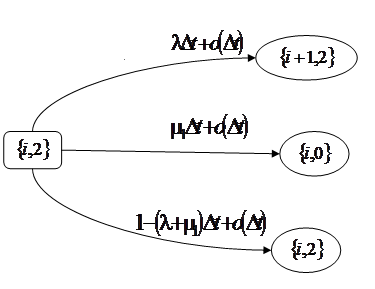Рис. 3.3 – Возможные переходы из состояния 
Рис. 3.4 – Возможные переходы из состояния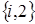 
Найти точное аналитическое решение системы (3.1) практически невозможно, но можно решить асимптотически в условиях большой задержки, то есть при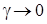 
.
Первое приближение
Для асимптотического решения системы (3.1) сделаем замену переменных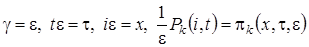 
. В результате замены производится переход от дискретной переменной 
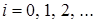к непрерывной переменной 
.
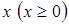В новых обозначениях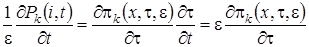 
. Тогда система (3.1) примет вид
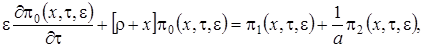
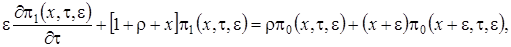(3.2)
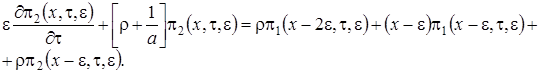
Получим вид решения системы (3.2), которую будем решать в два этапа.
1 этап. Считая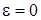 
и предполагая, что 
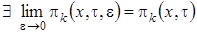, будем иметь
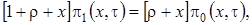(3.3)
.
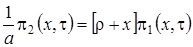Выразим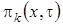 
через функцию 
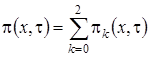и получим
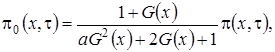
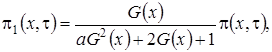(3.4)
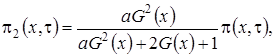
где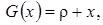 
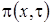- асимптотическая плотность нормированного числа заявок в источнике повторных вызовов.
Обозначим
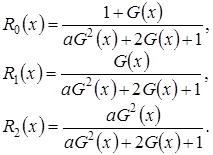(3.5)
Заметим, что из системы (3.3) следуют равенства
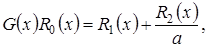
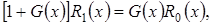(3.6)
.
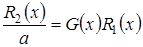Осталось найти вид функции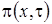 
. Для этого перейдем ко второму этапу.
2 этап. В системе (3.2) разложим функции по приращению аргумента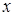 
, ограничиваясь слагаемыми порядка 
, получим систему
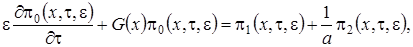
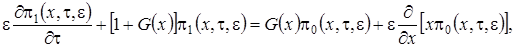(3.7)
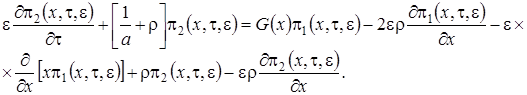
Просуммируем полученные уравнения, поделим на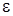 
и перейдем 
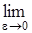. Тогда будем иметь
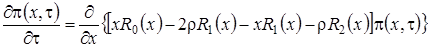. (3.8)
С учетом того, что
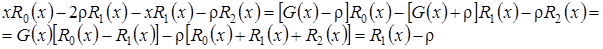
равенство (3.8) принимает вид
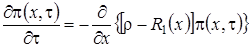. (3.9)
Таким образом мы получили, что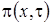 
удовлетворяет уравнению Фоккера-Планка с коэффициентом переноса равным 
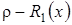, и нулевым коэффициентом диффузии. Из определения для коэффициента переноса можно сделать вывод, что 
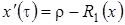, то есть 
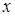зависит от времени и 
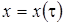– имеет смысл асимптотического среднего, в ее окрестности достаточно долго флуктуируют значения нормированного процесса 
.
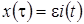Второе приближение
Зная асимптотическое среднее, найдем распределение вероятностей значений отклонения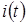 
от его среднего. Для этого в исходной системе уравнений (3.1) сделаем замену переменных 
, 
, 
, 
.
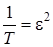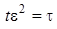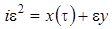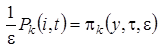В новых обозначениях производная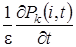 
равна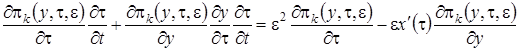 
.
Будем иметь
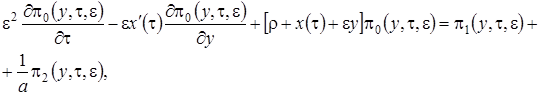
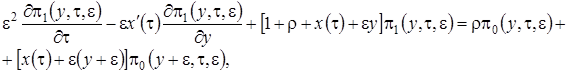(3.10)
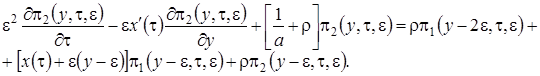
Решение системы (3.10) аналогично решению системы (3.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (3.10) положим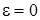 
и найдем решение в виде
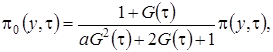
(3.11)
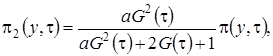
где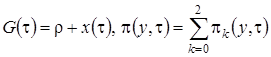 
– асимптотическое распределение нормированного числа заявок в источнике повторных вызовов в окрестности асимптотического среднего.
Перейдем ко второму этапу.
2 этап. Неизвестные функции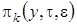 
будем искать с точностью до 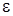форме
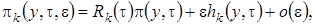(3.12)
где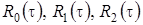 
имеют вид аналогичный (3.5), где в качестве 
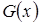выступает 
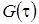и для них справедливы равенства (3.7).
Найдем вид функций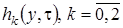 
.
С точностью до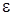 
(3.10) запишем
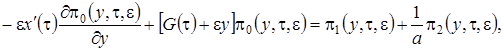
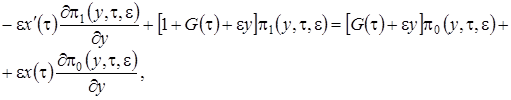(3.13)
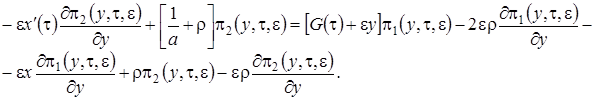
В уравнения (3.13) подставим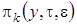 
в форме (3.12), уничтожим подобные слагаемые и получим систему неоднородных линейных алгебраических уравнений относительно функций 
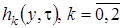вида
,
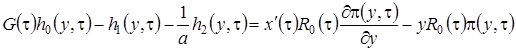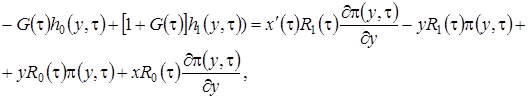, (3.14)
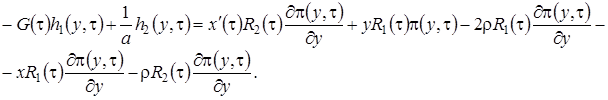
Система (3.14) будет иметь решение, если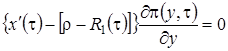 
. Из уравнения Фоккера-Планка (3.9) мы знаем, что 
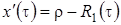. Таким образом, можно сделать вывод, что система (3.14) разрешима. При условии, что функция 
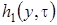известна, решение системы (3.14) можно записать так
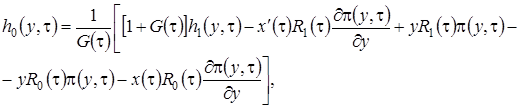(3.15)
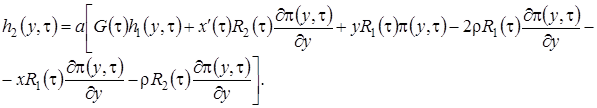
Перейдем к третьему этапу.
3 этап. С точностью до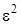 
уравнения (3.10) запишем следующим образом
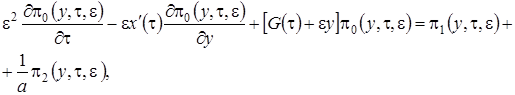
(3.16)
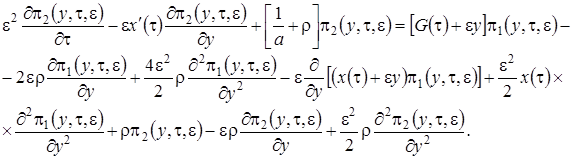
Теперь подставляем в систему уравнений (3.16)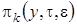 
в форме (3.12), оставляем слагаемые, имеющие порядок не выше 
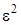и суммируем уравнения. Получим равенство для нахождения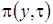 
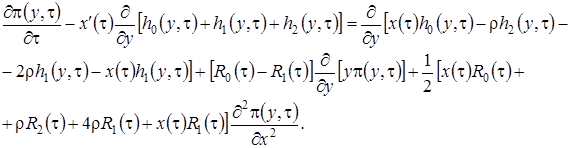(3.17)
В полученное равенство подставим выражения для функци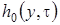и 
и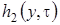 
, найденные на втором этапе. В результате приведения подобных, для 
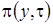получим уравнение Фоккера-Планка
(3.18)
с коэффициентом переноса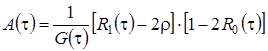 
и коэффициентом диффузии
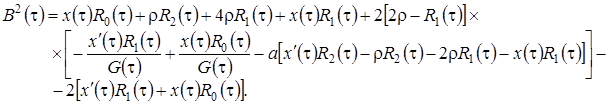
Уравнение Фоккера-Планка (3.18) получено для некоторого диффузионного процесса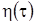 
, плотность распределения вероятностей которого 
.
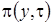Запишем стохастическое дифференциальное уравнение для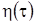 
в общей форме
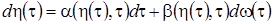, (3.19)
где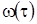 
- винеровский процесс с нулевым средним и единичным коэффициентом диффузии, в нашем случае оно приобретает вид
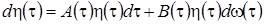. (3.20)
Введем новый случайный процесс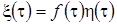 
, (3.21)
для его приращения справедливо
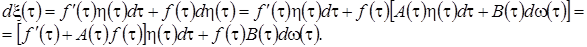
Выберем функцию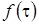 
так, чтобы она удовлетворяла дифференциальному уравнению 
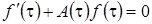. Например, 
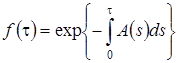. Тогда 
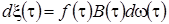и, следовательно, 
.
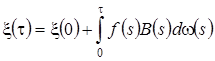Выразим из (3.21) функцию 
(заметим, что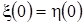 
) и получим
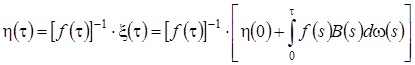(3.22)
Анализируя вид процесса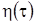 
можно сделать вывод, что он распределен по нормальному закону. Найдем 
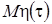и 
, которые полностью определяют вид плотности распределения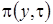 
. Учитывая свойства винеровского процесса, получим
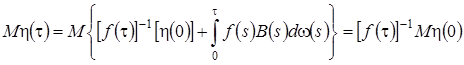(3.23)
Найдем дисперсию.
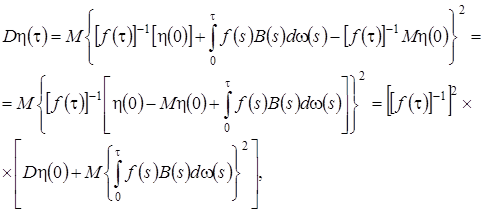
рассмотрим второе слагаемое подробнее. Для этого введем обозначение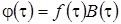 
, тогда получим
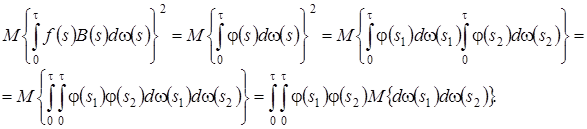
С учетом того, что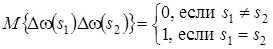 
будем иметь
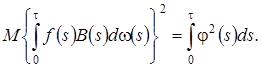
Тогда в окончательном варианте дисперсия равна
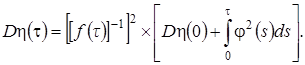(3.24)
Теперь можно записать решение уравнения Фоккера-Планка (3.18), которое имеет вид
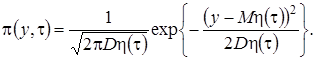(3.25)
Пусть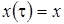 
, где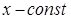 
- точка покоя дифференциального уравнения 
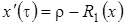, которая определяется конечным уравнением
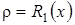, (3.26)
где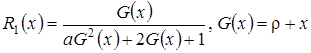 
.
Возможны три варианта:
1. 
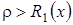, тогда точек покоя не существует (рис. 3.5).
2. 
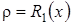, тогда существует одна точка покоя 
.
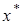3. 
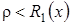, тогда существует две точки покоя 
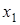и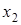 
.
Для примера рассмотрим случай, когда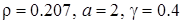 
(рис. 3.6). Тогда уравнение (3.26) имеет единственный корень 
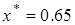. Коэффициенты диффузии уравнения Фоккера-Планка не зависят от времени и равны 
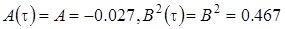. Если взять 
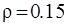, то уравнение (3.26) будет иметь два корня 
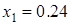и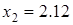 
(рис. 3.7). Для первой точки коэффициенты диффузии равны 
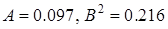, для второй 
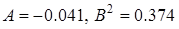. Точка 
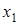является нежелательной. Если предположить, что сеть связи работает в стационарном режиме, то в окрестности точки 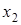распределение нормированного числа заявок в ИПВ является нормальным [1] и имеет вид
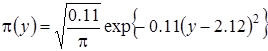, (3.27)
 | |||
| |||
|
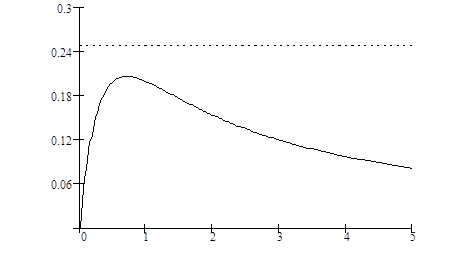
Рис. 3.5
|
|
|
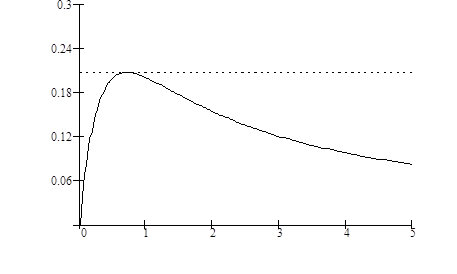
Рис. 3.6
|
|
|
|
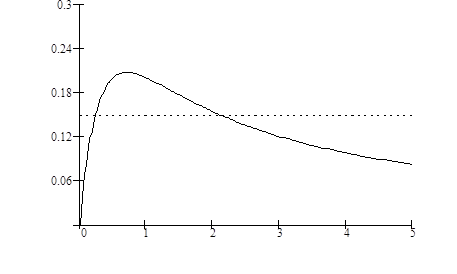
Рис. 3.7
Дата: 2019-07-24, просмотров: 202.
